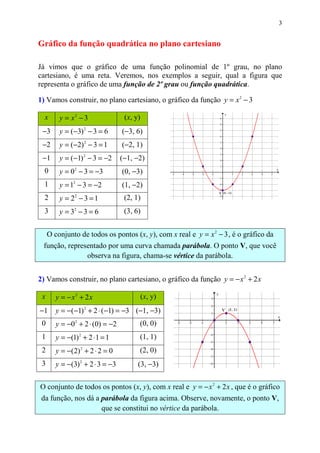
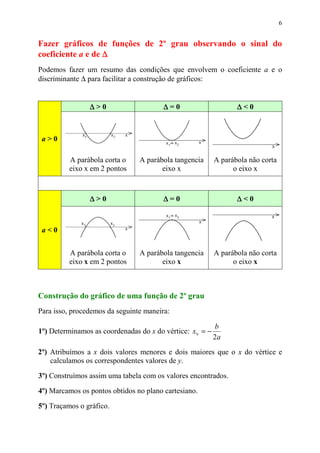
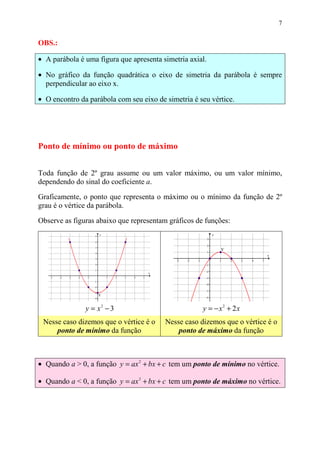
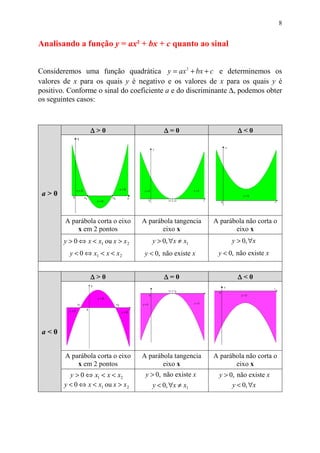
Este documento fornece uma introdução às funções polinomiais de 2o grau. Discute como Galileu Galilei usou funções quadráticas para descrever o movimento de objetos sob a gravidade. Também define funções quadráticas como qualquer função na forma y = ax2 + bx + c, e discute como calcular e interpretar os vértices, zeros, máximos e mínimos dessas funções.

1. Função polinomial de 2º grau
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
Como captar o movimento de uma bola de futebol chutada pelo goleiro? ...........................1
Reconhecer como função quadrática toda função definida pela equação y = ax² + bx + c ..... 1
Gráfico da função quadrática no plano cartesiano ................................................................3
Reconhecer e calcular o vértice da parábola .........................................................................4
Zeros ou raízes da função polinomial de 2º grau ..................................................................5
Estudando a concavidade da parábola...................................................................................5
Fazer gráficos de funções de 2º grau observando o sinal do coeficiente a e de ∆ ................6
Construção do gráfico de uma função de 2º grau...........................................................6
Ponto de mínimo ou ponto de máximo .................................................................................7
Analisando a função y = ax² + bx + c quanto ao sinal...........................................................8
Determinar os valores de x para os quais o sinal da função é positiva; negativa ou nula .....9
Resolver uma inequação de 2º grau na variável x ...............................................................13
Referências bibliográficas ...................................................................................................15

2. 1
FUNÇÃO POLINOMIAL DE 2º GRAU
Como captar o movimento de uma bola de futebol chutada pelo
goleiro?
O goleiro coloca a bola em jogo com um chute forte. A bola sobe até um ponto
máximo e começa a descer descrevendo, assim, uma curva que recebeu o nome
de parábola. O físico italiano Galileu Galilei, estudou atentamente movimentos
como o desta bola e concluiu que, se não fosse a resistência do ar, qualquer
corpo solto no campo de gravidade da Terra se movimentaria do mesmo modo.
Ou seja, ao fim de 1 segundo percorreria cerca de 5 ⋅ 12 = 5 metros; depois de 2
segundos, percorreria cerca de 5 ⋅ 2 2 = 20 metros; depois de 3 segundos,
5 ⋅ 9 2 = 45 metros; e assim sucessivamente. Desta forma, depois de x segundos,
percorreria 5 ⋅ x 2 metros, onde 5 é aproximadamente a metade da aceleração da
gravidade em metros por segundo, em cada segundo. Isto é o mesmo que
escrever a função f ( x) = y = 5 x 2 . Galileu agrupou todos esses elementos em um
importante conceito matemático: função quadrática. Toda função na qual a
variável x aparece com o expoente máximo igual a 2 é chamada de função
quadrática, ou função polinomial de 2º grau, pois o expoente máximo da
variável é o quadrado
Reconhecer como função quadrática toda função definida pela
equação y = ax² + bx + c
Função polinomial de 2º grau ou função quadrática é toda função definida
pela fórmula matemática y = ax 2 + bx + c , com a, b e c números reais e a ≠ 0 .
Assim, são funções polinomiais de 2º grau:
• y = x 2 + 4 x − 3 ( a = 1, b = 4, c = −3 )
• y = 2x 2 ( a = 2, b = 0, c = 0 )
• y = − x 2 + 5 ( a = −1, b = 0, c = 5 )

3. 2
Considerando as definições dadas e os conhecimentos que você já tem, observe
os exemplos:
a) Dado o número real 7, qual é a imagem pela função y = 3 x 2 − 4 x + 1 ?
Nesse caso temos x = 7.
y = 3x 2 − 4 x + 1
y = 3 ⋅ 72 − 4 ⋅ 7 + 1
y = 3 ⋅ 49 − 28 + 1
y = 147 − 28 + 1
y = 120
Logo, a imagem do número 7, pela função, é 120.
b) Dada a função definida por y = x 2 + 5 x − 4 , determinar o número real x cuja
imagem, pela função, é 20.
Nesse caso temos y = 20.
y = x 2 + 5x − 4 −b± ∆
x=
x 2 + 5x − 4 = y 2a
− 5 ± 121 − 5 + 11 6
x 2 + 5 x − 4 = 20 x= x′ = = =3
2 ⋅1 2 2
x 2 + 5 x − 24 = 0 − 5 ± 11
(a = 1, b = 5, c = 24) x=
2
∆ = b 2 − 4ac − 5 − 11 − 16
x′′ = = = −8
∆ = 5 − 4 ⋅ 1 ⋅ (−24)
2
2 2
∆ = 25 + 96
∆ = 121
Logo, temos x = −8 ou x = 3.

4. 3
Gráfico da função quadrática no plano cartesiano
Já vimos que o gráfico de uma função polinomial de 1º grau, no plano
cartesiano, é uma reta. Veremos, nos exemplos a seguir, qual a figura que
representa o gráfico de uma função de 2º grau ou função quadrática.
1) Vamos construir, no plano cartesiano, o gráfico da função y = x 2 − 3
x y = x2 − 3 (x, y)
−3 y = (−3) 2 − 3 = 6 (−3, 6)
−2 y = (−2) 2 − 3 = 1 (−2, 1)
−1 y = (−1) 2 − 3 = −2 (−1, −2)
0 y = 0 2 − 3 = −3 (0, −3)
1 y = 12 − 3 = −2 (1, −2)
2 y = 22 − 3 = 1 (2, 1)
3 y = 32 − 3 = 6 (3, 6)
O conjunto de todos os pontos (x, y), com x real e y = x 2 − 3 , é o gráfico da
função, representado por uma curva chamada parábola. O ponto V, que você
observa na figura, chama-se vértice da parábola.
2) Vamos construir, no plano cartesiano, o gráfico da função y = − x 2 + 2 x
x y = − x2 + 2x (x, y)
−1 y = −(−1) 2 + 2 ⋅ (−1) = −3 (−1, −3)
0 y = −0 2 + 2 ⋅ (0) = −2 (0, 0)
1 y = −(1) 2 + 2 ⋅ 1 = 1 (1, 1)
2 y = −(2) 2 + 2 ⋅ 2 = 0 (2, 0)
3 y = −(3) 2 + 2 ⋅ 3 = −3 (3, −3)
O conjunto de todos os pontos (x, y), com x real e y = − x 2 + 2 x , que é o gráfico
da função, nos dá a parábola da figura acima. Observe, novamente, o ponto V,
que se constitui no vértice da parábola.

5. 4
Reconhecer e calcular o vértice da parábola
Você pode notar a existência de um vértice em cada parábola que foi construída
nos exemplos dados. Pode-se calcular o vértice de uma parábola da seguinte
forma:
b
• Calcula-se o valor x do vértice: xV = −
2a
• Substitui-se o valor de x na função e encontra-se o valor de y do vértice ( yV )
► No Exemplo 1 do item anterior temos:
y = x 2 − 3 ( a = 1, b = 0, c = −3 )
b −0
• xV = − = =0
2a 2
• y = x 2 − 3 = 0 2 − 3 = −3
Portanto, a coordenada do vértice é V (0, −3).
► No Exemplo 2 do item anterior temos:
y = − x 2 + 2 x ( a = −1, b = 2, c = 0 )
b −2
• xV = − = =1
2a − 2
• y = − x 2 + 2 x = −12 + 2 ⋅1 = 1
Portanto, a coordenada do vértice é V (1, 1).

6. 5
Zeros ou raízes da função polinomial de 2º grau
As raízes ou zeros de uma função são os pontos onde seu gráfico corta o eixo x.
Na função de 2º grau y = ax 2 + bx + c , se y = 0 obtemos a equação
ax 2 + bx + c = 0 .
Algebricamente, os zeros da função quadrática são obtidos quando resolvemos a
equação de 2º grau ax 2 + bx + c = 0 . O discriminante (∆) da equação é, também,
o discriminante da função:
• Se ∆ > 0, a função y = ax 2 + bx + c tem dois zeros reais diferentes
• Se ∆ = 0, a função y = ax 2 + bx + c tem dois zeros reais iguais
• Se ∆ > 0, a função y = ax 2 + bx + c não tem dois zeros reais
Exemplo:
a) Determine, algebricamente, os zeros da função y = x 2 + 5 x + 6 .
x 2 + 5x + 6 = 0
Basta resolver a equação aplicando a fórmula de Bháskara.
Acharemos que x′ = −3 e x′′ = −2 . Portanto, os zeros ou raízes da função
polinomial de 2º grau são −3 e −2.
Estudando a concavidade da parábola
Antes de construir o gráfico da função y = ax 2 + bx + c , é possível saber como
será a sua concavidade. Basta observar o sinal do coeficiente a:
Se a > 0 (a positivo), a concavidade Se a < 0 (a negativo), a concavidade
estará voltada para cima estará voltada para baixo

7. 6
Fazer gráficos de funções de 2º grau observando o sinal do
coeficiente a e de ∆
Podemos fazer um resumo das condições que envolvem o coeficiente a e o
discriminante ∆ para facilitar a construção de gráficos:
∆>0 ∆=0 ∆<0
a>0
A parábola corta o A parábola tangencia A parábola não corta
eixo x em 2 pontos eixo x o eixo x
∆>0 ∆=0 ∆<0
a<0
A parábola corta o A parábola tangencia A parábola não corta
eixo x em 2 pontos eixo x o eixo x
Construção do gráfico de uma função de 2º grau
Para isso, procedemos da seguinte maneira:
b
1º) Determinamos as coordenadas do x do vértice: xV = −
2a
2º) Atribuímos a x dois valores menores e dois maiores que o x do vértice e
calculamos os correspondentes valores de y.
3º) Construímos assim uma tabela com os valores encontrados.
4º) Marcamos os pontos obtidos no plano cartesiano.
5º) Traçamos o gráfico.

8. 7
OBS.:
• A parábola é uma figura que apresenta simetria axial.
• No gráfico da função quadrática o eixo de simetria da parábola é sempre
perpendicular ao eixo x.
• O encontro da parábola com seu eixo de simetria é seu vértice.
Ponto de mínimo ou ponto de máximo
Toda função de 2º grau assume ou um valor máximo, ou um valor mínimo,
dependendo do sinal do coeficiente a.
Graficamente, o ponto que representa o máximo ou o mínimo da função de 2º
grau é o vértice da parábola.
Observe as figuras abaixo que representam gráficos de funções:
y = x2 − 3 y = − x2 + 2x
Nesse caso dizemos que o vértice é o Nesse caso dizemos que o vértice é o
ponto de mínimo da função ponto de máximo da função
• Quando a > 0, a função y = ax 2 + bx + c tem um ponto de mínimo no vértice.
• Quando a < 0, a função y = ax 2 + bx + c tem um ponto de máximo no vértice.

9. 8
Analisando a função y = ax² + bx + c quanto ao sinal
Consideremos uma função quadrática y = ax 2 + bx + c e determinemos os
valores de x para os quais y é negativo e os valores de x para os quais y é
positivo. Conforme o sinal do coeficiente a e do discriminante ∆, podemos obter
os seguintes casos:
∆>0 ∆=0 ∆<0
a>0
A parábola corta o eixo A parábola tangencia A parábola não corta o
x em 2 pontos eixo x eixo x
y > 0 ⇔ x < x1 ou x > x2 y > 0, ∀x ≠ x1 y > 0, ∀x
y < 0 ⇔ x1 < x < x 2 y < 0, não existe x y < 0, não existe x
∆>0 ∆=0 ∆<0
a<0
A parábola corta o eixo A parábola tangencia A parábola não corta o
x em 2 pontos eixo x eixo x
y > 0 ⇔ x1 < x < x2 y > 0, não existe x y > 0, não existe x
y < 0 ⇔ x < x1 ou x > x2 y < 0, ∀x ≠ x1 y < 0, ∀x

10. 9
Determinar os valores de x para os quais o sinal da função é
positiva; negativa ou nula
Consideremos os seguintes exemplos:
1) Dada a função y = x 2 − 2 x − 8 , verifique quais são os valores reais de x para
que se tenha:
a) y = 0 b) y > 0 c) y < 0
Inicialmente, vamos analisar o coeficiente a e o discriminante ∆ da função para
podermos fazer um esboço do gráfico da função:
Como a = 1 > 0, a parábola tem a concavidade voltada para cima.
∆ = b 2 − 4ac = (−2) 2 − 4 ⋅ 1 ⋅ (−8) = 4 + 32 = 36 > 0
Então, a parábola corta o eixo x em dois pontos.
−b± ∆
x=
2a
− (−2) ± 36 2+6 8
x= x′ = = =4
2 ⋅1 2 2
2±6
x=
2
2−6 −4
x′′ = = = −2
2 2
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
y = 0 para x = −2 ou x = 4
y > 0 para o intervalo {x ∈ / x < −2 ou x > 4}
y < 0 para o intervalo {x ∈ / −2 < x < 4}

11. 10
2) Dada a função y = x 2 − 4 x + 4 , verifique quais são os valores reais de x para
os quais vamos ter:
a) y = 0
b) y > 0
c) y < 0
Inicialmente, vamos analisar o coeficiente a e o discriminante ∆ da função para
podermos fazer um esboço do gráfico da função:
Como a = 1 > 0, a parábola tem a concavidade voltada para cima.
∆ = b 2 − 4ac = (−4) 2 − 4 ⋅1 ⋅ 4 = 16 − 16 = 0
Então, a parábola tangencia eixo x.
−b± ∆
x=
2a
− (−4) ± 0
x=
2 ⋅1
4±0 4
x= x′ = x′′ = =2
2 2
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
y = 0 para x = 2
y > 0 para o intervalo {x ∈ / x ≠ 2}
y nunca será negativo

12. 11
3) Dada a função y = − x 2 + 2 x − 10 , determine para quais valores reais de x
vamos ter:
a) y = 0
b) y > 0
c) y < 0
Inicialmente, vamos analisar o coeficiente a e o discriminante ∆ da função para
podermos fazer um esboço do gráfico da função:
Como a = −1 < 0, a parábola tem a concavidade voltada para baixo.
∆ = b 2 − 4ac = 2 2 − 4 ⋅ (−1) ⋅ (−10) = 4 − 40 = −36 < 0
Então, a parábola não corta o eixo x.
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
Nesse caso, y será sempre negativo para
qualquer valor real de x

13. 12
4) Para quais valores reais de x a função y = −5 x 2 + 4 x + 1 é positiva?
Inicialmente, vamos analisar o coeficiente a e o discriminante ∆ da função para
podermos fazer um esboço do gráfico da função:
Como a = −5 < 0, a parábola tem a concavidade voltada para baixo.
∆ = b 2 − 4ac = 4 2 − 4 ⋅ (−5) ⋅ 1 = 16 + 20 = 36 > 0
Então, a parábola corta o eixo x em dois pontos.
−b± ∆
x=
2a
− 4 ± 36 −4+6 2 1
x= x′ = = =−
2 ⋅ (−5) − 10 − 10 5
−4±6
x=
− 10
− 4 − 6 − 10
x′′ = = =1
− 10 − 10
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
/ − < x <1
1
y > 0 para o intervalo ∈
5

14. 13
Resolver uma inequação de 2º grau na variável x
Consideremos os seguintes exemplos:
1) Resolver a inequação − 9 x 2 + 6 x − 1 < 0 .
A inequação dada é uma inequação de 2º grau na incógnita x.
Para resolvê-la, vamos aplicar o que aprendemos com a análise da função
quadrática quanto ao sinal. Assim, temos:
Como a = −9 < 0, a parábola tem a concavidade voltada para baixo.
∆ = b 2 − 4ac = 6 2 − 4 ⋅ (−9) ⋅ (−1) = 36 − 36 = 0
Então, a parábola tangencia o eixo x.
−b± ∆
x=
2a
−6± 0
x=
2 ⋅ (−9)
−6±0 −6 1
x= x′ = x′′ = =
− 18 − 18 3
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
Como a inequação nos pede valores reais de x
tais que y < 0, podemos dizer que a solução
dessa inequação é:
/
1
S= ∈
3

15. 14
2) Determinar os valores reais de x para os quais o produto ( x − 7)( x + 3) é maior
que 11.
Através do problema apresentado temos:
( x − 7)( x + 3) > 11
x 2 + 3 x − 7 x − 21 − 11 > 0
x 2 − 4 x − 32 > 0 → inequação do 2º grau
Como a = 1 > 0, a parábola tem a concavidade voltada para cima.
∆ = b 2 − 4ac = (−4) 2 − 4 ⋅ 1 ⋅ (−32) = 16 + 128 = 144 > 0
Então, a parábola corta o eixo x em dois pontos.
−b± ∆
x=
2a
− (−4) ± 144 4 + 12 16
x= x′ = = =8
2 ⋅1 2 2
4 ± 12
x=
2
4 − 12 − 8
x′′ = = = −4
2 2
Pelo que obtivemos, podemos fazer o esboço do gráfico e dar a resposta.
Esboço:
Como a inequação nos pede valores reais de x
para os quais temos y > 0, podemos dizer que
a solução dessa inequação é:
S = {x ∈ / x < −4 ou x > 8}
Então, o produto ( x − 7)( x + 3) é maior que
11 para {x ∈ / x < −4 ou x > 8}

16. 15
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
KLICK EDUCAÇÃO: O PORTAL DA EDUCAÇÃO. Disponível em:
<http://www.klickeducacao.com.br>. Acesso em: 21 de agosto de 2008.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.
TUTOMANIA: MANÍACOS POR CONHECIMENTO. Disponível em:
<http://tutomania.com.br>. Acesso em: 24 de agosto de 2008.