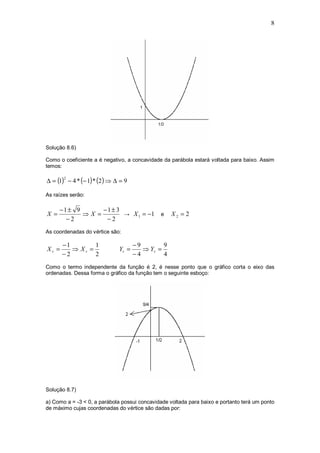
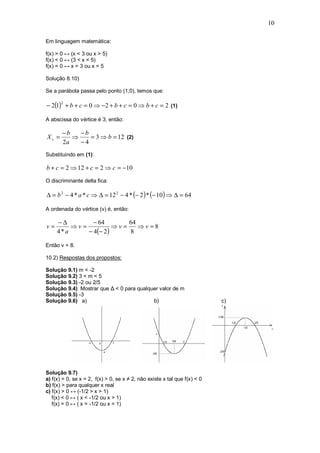
1) O documento discute funções quadráticas, definidas como f(x) = ax2 + bx + c. É apresentada a fórmula de Bhaskara para calcular raízes e as expressões para obter as coordenadas do vértice. 2) É descrito um experimento usando um sensor de movimento para medir a trajetória parabólica de um objeto lançado verticalmente. 3) São fornecidos exercícios resolvidos e propostos sobre funções quadráticas, incluindo cálculo de raízes, gráficos

1. 1
MATEMÁTICA – FUNÇÕES
1) A FUNÇÃO DO SEGUNDO GRAU OU FUNÇÃO QUADRÁTICA
2) Objetivo:
O objetivo desse tema é estudar a função do segundo grau ou função quadrática, seus gráficos
e condições de existência da referida função.
3) Introdução:
A função do segundo grau, ou função quadrática, ou ainda função polinomial do segundo grau,
como também é chamada, é toda função de R em R dada pela seguinte lei:
f ( x ) = ax 2 + bx + c
Onde a, b e c são números reais e a ≠ 0.
Alguns exemplos de função do segundo grau:
f ( x ) = 2 x 2 + 3 x + 5 , a = 2, b = 3 e c = 5
f ( x ) = 3 x 2 − 4 x + 1 , a = 3, b = -4 e c = 1
f ( x ) = − x 2 + 3 x − 5 , a = -1, b = 3 e c = -5
O gráfico de toda função do segundo grau é uma parábola, onde sua concavidade pode estar
voltada para cima ou para baixo, dependendo do valor do coeficiente “a”. Se este coeficiente
for positivo, a concavidade estará voltada para cima, caso o coeficiente “a” seja negativo, a
concavidade estará voltada para baixo.
Raízes ou zeros da função:
Raízes ou zeros da função são os valores da variável independente x que tornam a função
igual a zero. Para determiná-las devemos igualar a função a zero, assim devemos fazer
ax 2 + bx + c = 0 . Então utilizamos a fórmula de Bhaskara para o cálculo das raízes.
A fórmula de Bhaskara tem a seguinte expressão:
−b± ∆
x=
2a
Onde:
∆ = b 2 − 4ac
Uma observação importante é saber quantas raízes reais a função de segundo grau possuirá.
Esta análise é feita analisando o valor do discriminante delta, a saber:
Se ∆ > 0, há duas raízes reais e distintas.
Se ∆ = 0, há somente uma raiz real (Na verdade há duas, mas elas são iguais)
Se ∆ < 0, não há raiz real.

2. 2
Coordenadas do Vértice:
As coordenadas do vértice da parábola são calculadas com as seguintes expressões:
Abscissa do Vértice:
−b
Xv =
2a
Ordenada do Vértice:
−∆
Yv =
4a
Para construirmos o gráfico de uma função do segundo grau, precisamos apenas desses
quatro valores, ou seja, as duas raízes e as coordenadas do vértice da parábola.
Como exemplo, vejamos como ficaria o gráfico da função do segundo grau definida por:
f (x ) = x 2 + x :
As raízes da função são calculadas igualando a função à zero:
x2 + x = 0
O discriminante delta fica:
∆ = (1) − 4(1)(0) = 1
2
As raízes ficam:
−1± 1
x=
2
Com isso as raízes são:
x1 = 0 e x2 = -1
As coordenadas do vértice ficam:
Xv = -1/2 e Yv = -1/4
Assim o gráfico da função tem a seguinte forma:

3. 3
4) Material utilizado:
Para este tópico realizaremos uma experiência de lançamento vertical de um corpo, que
descreve uma trajetória parabólica, que marca sua posição com o passar do tempo. Para tanto
será utilizado o sensor de movimento KDS-1042, da VOLTCOM, que faz parte do kit da
Science Cube, a interface para ser ligada ao computador, e, um objeto que possa ser solto em
queda livre, e que tenha seu movimento detectado pelo sensor, como uma bolinha de ping
pong, ou uma tampa de recipiente plástico (recomendado), por exemplo.
5) Procedimento:
O procedimento para o experimento é bastante simples.
5.1) Conecte o a interface com o PC pela porta USB
5.2) Conecte o sensor de movimento à interface
5.3) Ligue o PC e a interface
5.4) Posicione o objeto a ser solto em queda livre acima do sensor, de modo que este possa
detectar seu movimento.
5.5) Dispare o botão de iniciar o experimento
5.6) Lance o objeto de uma altura superior a 40 cm para que seu movimento comece a ser
detectado pelo sensor de movimento.
Recomenda-se que o objeto a ser lançado esteja bem acima do sensor de posição, e que o
mesmo, seja lançado o mais verticalmente possível. Nem sempre isso é conseguido de
maneira satisfatória, pois é muito difícil lançá-lo numa trajetória exatamente retilínea, por isso, a
recomendação anterior de se utilizar uma tampa de recipiente plástico com um raio razoável.
Assim que o objeto comece a queda, sua posição ao longo da queda com o tempo pode ser
visualizada no gráfico do Excel.
6) Resultados:
O gráfico do experimento, que foi detectado pelo sensor de posição (ou movimento) e
transferido para o Excel, pode ser visualizado a seguir.
7-) Conclusões/Comentários:
Nota-se pelo gráfico que o movimento do objeto é ascendente até o instante de
aproximadamente 4 segundos, atingindo uma altura de 1,6 metros. Após esse instante o objeto
começa a cair em queda livre.
Outro fato a ser observado é que o gráfico não é muito parecido com uma parábola, pois é
muito difícil lançar o referido objeto, de forma que ele fique posicionado exatamente acima do
sensor de posição, o mesmo normalmente sai da área de abrangência do sensor, com isso há
2
um corte na captação do movimento, que deveria obedecer à função S = S0 + V0T + aT /2, por
isso o gráfico não tem a forma exata de uma parábola.

4. 4
8) Exercícios resolvidos:
8.1) Identifique os coeficientes a, b, c das seguintes funções quadráticas:
x 2 − 10 x + 3
a) f ( x ) = x − 3 x + 10 b) f ( x ) = 3 x − 9 c) f ( x ) =
2 2
5
8.2) Determine m a fim de que a função f, definida por f (x ) = (m − 1)x + 2 x − 3 , seja do
2
segundo grau.
8.3) Determine os valores de p para que a função real f, definida por
( )
f ( x ) = p 2 − 5 p + 4 x 2 − 4 x + 5 , seja do segundo grau.
8.4) Calcule as raízes das seguintes funções:
2
a) f(x) = x -5x + 6
2
b) f(x) = 4x -4x +1
8.5) Esboce os gráficos das funções do exercício anterior.
2
8.6) Esboce o gráfico da função de segundo grau definida por f(x) = -x +x +2
8.7) Uma bala é atirada de um canhão de brinquedo (como mostra a figura) e descreve uma
parábola de acordo com a função y = −3 x + 60 x (onde x e y são medidos em metros).
2
Vamos determinar:
a) A altura máxima atingida pela bola.
b) O alcance do disparo.
8.8) Determine o valor m na função real f ( x ) = 3 x − 2 x + m para que o valor mínimo seja
2
5/3.
8.9) Estude o sinal da função definida por f ( x ) = x − 8 x + 15 .
2
8.10) A parábola de equação y = − x + bx + c passa pelo ponto (1;0) e seu vértice é o ponto
2
de coordenadas (3;v). Determine v.
9) Exercícios propostos:
9.1) Determine m para que a parábola representativa da função f ( x ) = (2 + m )x + 5 x + 3
2
tenha concavidade voltada para baixo.
9.2) Determine os valores de m para que a função definida por
( )
f ( x ) = m − 8m + 15 x − 5 x + 8 tenha concavidade voltada para baixo.
2 2
9.3) Determine os valores de m para que a função quadrática
( )
f ( x ) = x + (3m + 2 )x + m + m + 2 tenha um zero real duplo.
2 2

5. 5
9.4) Mostre que para qualquer valor real não nulo do parâmetro m a função quadrática
f ( x ) = mx 2 − 2mx + 3m não apresenta raízes reais.
9.5) Determine o parâmetro m na função quadrática f ( x ) = x + mx + m − m − 12 , de
2
( 2
)
modo que a mesma possua uma raiz nula e outra positiva.
9.6) Construa o gráfico de cada uma das funções quadráticas dadas a seguir:
a-) f ( x ) = x − 4 b-) f ( x ) = 2 x − 5 x + 2 c-) f ( x ) = − x + x −
2 2 2 2
9
9.7) Faça o estudo dos sinais das seguintes funções quadráticas:
a) f ( x ) = x − 4 x + 4 b-) f ( x ) = 3 x − 4 x + 2 c-) f (x ) = − x +
1 1
2 2 2
x+
2 2
9.8) Determine o valor do parâmetro m da função real f (x ) = mx + (m − 1)x + (m + 2 ) para
2
que o valor máximo (ordenada do vértice) seja igual a 2.
9.9) O gráfico da função quadrática definida por f ( x ) = x − mx + (m − 1) , onde m é real,
2
possui um único ponto em comum com o eixo das abscissas. Então, qual o valor que a função
associa a x = 2?
9.10) Na figura a seguir, a parábola de vértice V é o gráfico da função quadrática
____ _____
f ( x ) = x 2 + bx + c . Sendo OA = 2 OV e a abscissa de V diferente de zero, quais os valores
de b e c ?
10) Solução dos Exercícios resolvidos e respostas dos propostos:
10.1) Solução dos exercícios resolvidos:
Solução 8.1)Para se identificar os coeficientes a, b, c das funções quadráticas devemos
compará-las com a forma genérica das funções de segundo grau f(x) = ax2 +bx +c. Assim
temos:
a) a = 1, b = -3, c = 10
b) a = 3, b = 0, c = -9
c) Aqui devemos distribuir o denominador da função entre os numeradores, assim temos:
x 2 10 x 3
f (x ) = − +
5 5 10
Com isso temos:

6. 6
a = 1/5, b = -2, c = 3/10
Solução 8.2)Para que uma função do tipo f ( x ) = ax + bx + c seja do segundo grau, seu
2
coeficiente a deve ser diferente de zero. Com isso vem:
m −1 ≠ 0 ⇒ m ≠ 1
Solução 8.3)Como no exercício anterior, temos:
p2 − 5p + 4 ≠ 0
Nesse caso devemos resolver a inequação do segundo grau e analisar o sinal da função, na
qual o coeficiente a da função original está sendo determinado.
Relembrando que para resolver uma equação do segundo grau, devemos lançar mão da
fórmula de Báskara, assim temos:
∆ = b 2 − 4ac ⇒ Α = (− 5) − 4(1)(4 ) ⇒ ∆ = 9
2
−b± ∆ − (− 5) ± 9 5±3
p= ⇒ p= ⇒ p= ⇒ p1 = 4, p 2 = 1
2a 2 2
As raízes da equação são 1 e 4. Analisando o sinal da função que está determinando o
coeficiente a da função original, temos:
Com isso notamos que, para a função original ser do segundo grau, os valores de p devem ser
tais que:
p < 1, ou p>4
Solução 8.4)
a) Utilizando a formula de Bhaskara temos:
∆ = (− 5) − 4 * (1) * (6) ⇒ ∆ = 1
2
As raízes ficam:
− (− 5) ± 1
x=
2
X1 = 2 e X2 = 3
b) Com o mesmo procedimento do item anterior temos:
∆ = (− 4 ) − 4 * (4 ) * (1) ⇒ ∆ = 0
2
Assim as raízes são:

7. 7
− (− 4 ) ± 0 4±0
x= ⇒x=
2*4 8
Com isso temos as raízes:
X1 = 1/2 e X2 = 1/2
Solução 8.5)
a) As raízes já estão calculadas no exercício anterior, falta saber quais são as coordenadas do
vértice. Como o discriminante delta é 1, temos:
Xv = -(-5)/2 → Xv = 5/2 Yv = -1/4
Aqui, temos também o ponto em que o gráfico cruza o eixo das ordenadas, que é o termo
independente da função, nesse caso o 6. Dessa forma o gráfico da função fica da seguinte
maneira:
b) Como no caso anterior, as raízes já foram calculadas no exercício anterior. As coordenadas
do vértice ficam:
Xv = -(-4)/2*4 → Xv = ½ Y v = -0/4*4 → Yv = 0.
O termo independente da função é 1, então é nesse ponto que o gráfico cruza o eixo das
ordenadas. Assim, o gráfico da função fica:

8. 8
Solução 8.6)
Como o coeficiente a é negativo, a concavidade da parábola estará voltada para baixo. Assim
temos:
∆ = (1) − 4 * (− 1) * (2 ) ⇒ ∆ = 9
2
As raízes serão:
−1± 9 −1± 3
X = ⇒X = → X 1 = −1 e X2 = 2
−2 −2
As coordenadas do vértice são:
−1 1 −9 9
Xv = ⇒ Xv = Yv = ⇒ Yv =
−2 2 −4 4
Como o termo independente da função é 2, é nesse ponto que o gráfico corta o eixo das
ordenadas. Dessa forma o gráfico da função tem o seguinte esboço:
Solução 8.7)
a) Como a = -3 < 0, a parábola possui concavidade voltada para baixo e portanto terá um ponto
de máximo cujas coordenadas do vértice são dadas por:

9. 9
∆ = (60 ) − 4 * (− 3) * (0 ) ⇒ ∆ = 3600
2
− 60 − 3600
Xv = ⇒ X v = 10 Yv ⇒ Yv = 300
−6 − 12
Assim, a altura máxima atingida pela bala é de 300 metros.
b) A bola toca o solo quando y = 0. Assim, basta calcular as raízes da função. Com isso temos:
− 60 ± 3600 − 60 ± 60
X = ⇒X =
−6 −6
Dessa forma temos os valores X1 = 0 ou X2 = 20
O resultado X = 0 não convém, pois representa o ponto inicial da trajetória do projétil. Então, o
alcance do disparo é de 20 metros.
Solução 8.8) O valor mínimo da função é representado pela coordenada da ordenada do
vértice da parábola.
∆ = b 2 − 4 * a * c ⇒ ∆ = (− 2 ) − 4 * 3 * m ⇒ ∆ = 4 − 12m
2
−∆ 5 − (4 − 12m ) 5 12m − 4 36m − 12
Yv = ⇒ = ⇒ = ⇒ =5
4*a 3 4*3 3 12 12
3m − 1 = 5 ⇒ 3m = 6 ⇒ m = 2
Então para que a função tenha seu mínimo valor em 5/3, o termo independente m deve ser
igual a 2.
Solução 8.9) Estudar o sinal de uma função é saber onde a função torna-se positiva, negativa e
nula. Assim, apenas sabendo suas raízes podemos fazer o esboço de seu gráfico para
estudarmos seu sinal. Calculando as raízes da função dada temos:
∆ = b 2 − 4 * a * c ⇒ ∆ = (− 8) − 4 * 1 * 15 ⇒ ∆ = 64 − 60 ⇒ ∆ = 4
2
−b± ∆ 8± 4 8±2
X = ⇒X = ⇒X = X1 = 3 , X2 = 5
2*a 2 2
A parábola possui concavidade para cima, pois o coeficiente a = 1 > 0.
Assim, temos o esboço do gráfico sem nos preocuparmos com os valores máximos e mínimos:
Notamos então que a função torna-se positiva para valores de x menores do que 3 e maiores
do que 5, torna-se negativa para valores de x compreendidos entre 3 e 5, e torna-se nula
exatamente nos valores 3 e 5, pois essas são as raízes da função.

10. 10
Em linguagem matemática:
f(x) > 0 ↔ (x < 3 ou x > 5)
f(x) < 0 ↔ (3 < x < 5)
f(x) = 0 ↔ x = 3 ou x = 5
Solução 8.10)
Se a parábola passa pelo ponto (1;0), temos que:
− 2(1) + b + c = 0 ⇒ −2 + b + c = 0 ⇒ b + c = 2 (1)
2
A abscissa do vértice é 3, então:
−b −b
Xv = ⇒ = 3 ⇒ b = 12 (2)
2a −4
Substituindo em (1):
b + c = 2 ⇒ 12 + c = 2 ⇒ c = −10
O discriminante delta fica:
∆ = b 2 − 4 * a * c ⇒ ∆ = 12 2 − 4 * (− 2 ) * (− 10 ) ⇒ ∆ = 64
A ordenada do vértice (v) é, então:
−∆ − 64 64
v= ⇒v= ⇒v= ⇒v=8
4*a − 4(− 2 ) 8
Então v = 8.
10.2) Respostas dos propostos:
Solução 9.1) m < -2
Solução 9.2) 3 < m < 5
Solução 9.3) -2 ou 2/5
Solução 9.4) Mostrar que ∆ < 0 para qualquer valor de m
Solução 9.5) -3
Solução 9.6) a) b) c)
Solução 9.7)
a) f(x) = 0, se x = 2, f(x) > 0, se x ≠ 2, não existe x tal que f(x) < 0
b) f(x) > para qualquer x real
c) f(x) > 0 ↔ (-1/2 > x > 1)
f(x) < 0 ↔ ( x < -1/2 ou x > 1)
f(x) = 0 ↔ ( x = -1/2 ou x = 1)

11. 11
Solução 9.8) -1
Solução 9.9) 0
Solução 9.10) b = -4, c = 4