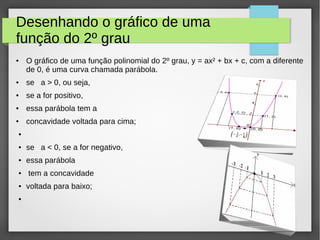
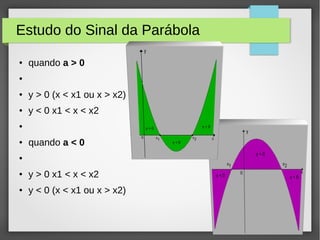
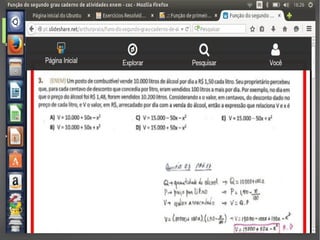
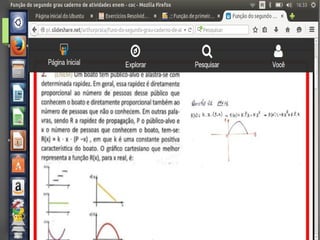
O documento descreve as funções quadráticas, definindo-as como funções polinomiais do 2o grau da forma f(x) = ax2 + bx + c. Explica como identificar os parâmetros a, b e c de funções quadráticas, e como determinar propriedades como raízes, vértice e concavidade com base nesses parâmetros. Apresenta também exercícios resolvidos sobre o assunto.

1. Função Quadrática
A função quadrática é uma função polinomial
do 2º grau, é qualquer função f de IR em IR dada
por uma lei da forma f(x) = ax² + bx + c, onde a,
b e c são números reais e a é diferente de 0.
Vejamos alguns exemplos de função quadráticas:
1 -f(x) = 3x² - 4x + 1, onde a = 3, b = - 4 e c =1
2 -f(x) = x² -1, onde a = 1, b = 0 e c = -1
3-f(x) = 2x² + 3x + 5, onde a = 2, b = 3 e c = 5
4-f(x) = - x² + 8x, onde a = -1, b = 8 e c = 0
5-f(x) = -4x², onde a = - 4, b = 0 e c = 0

2. Exercício 1: Identifique com um x as funções quadráticas
abaixo e indique quais os valores de a, b e c,
respectivamente.
( ) f(x) = 7x² +x a = b = c =
( ) f(x) = x³ -x² + 6x a = b = c =
( ) f(x) = (2-x)² + 3x³ + 5 a = b = c =
( ) f(x) = - x + 8x² -9 a = b = c =
( ) f(x) = x² a = b = c =
( ) f(x) = (2-x)² a = b = c =
( ) f(t) = 8 -9t + 5t² a = b = c =
( ) f(p) = p² - 4 a = b = c =

3. Desenhando o gráfico de uma
função do 2º grau
● O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c, com a diferente
de 0, é uma curva chamada parábola.
● se a > 0, ou seja,
● se a for positivo,
● essa parábola tem a
● concavidade voltada para cima;
●
● se a < 0, se a for negativo,
● essa parábola
● tem a concavidade
● voltada para baixo;
●

4. Exercício 2: Identifique com base no estudo do sinal de
a, quais das funções quadráticas abaixo possuem
concavidade para cima e para baixo.
( ) h(x) = 7x² +x
( ) f(x) = -x² + 6x
( ) g(x) = (2-x)² + 3x + 5
( ) f(x) = - x + 8x² -9
( ) f(x) = x²
( ) f(x) = (2+x)²
( ) f(t) = 8 -9t + 5t²
( ) f(p) = p² - 4

5. O Zero da função é obtido resolvendo a Equação do 2º
Grau associada à função
● Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² +
bx + c , com a diferente de 0, os números reais x tais que f(x) = 0. Ou
seja, as raízes da função f(x) = ax² + bx + c são as soluções da equação
do 2º grau:
ax² + bx + c = 0, as quais são dadas pela chamada fórmula de
Bhaskara:
● Delta = b² - 4*a*c
● Quando Delta > 0, é positivo, há duas raízes reais e distintas;
● x1 = (-b + raiz quadrada de Delta) / 2*a
● X2 = (-b - raiz quadrada de Delta) / 2*a
Quando Delta = 0, é zero, há só uma raiz real (para ser mais preciso, há
duas raízes iguais);
● x = -b / 2*a
● Quando Delta < 0, é negativo, não há raiz real.

6. Exercício 3: Identifique com base no estudo do Delta da
equação do segundo grau associada a cada função
quadrática, quais delas possuem uma, duas ou nenhuma raiz
real, após isto encontre o valor das raízes reais das funções
que possuam.
( ) h(x) = 7x² +x
( ) f(x) = -x² + 6x
( ) g(x) = (2-x)² + 3x + 5
( ) f(x) = - x + 8x² -9
( ) f(x) = x²
( ) f(x) = (2+x)²
( ) f(t) = 8 -9t + 5t²
( ) f(p) = p² - 4

7. Vértice
● Coordenadas do vértice da parábola
● Quando a > 0, a parábola tem concavidade voltada para
cima e um ponto de mínimo V;
● quando a < 0, a parábola tem concavidade voltada para
baixo e um ponto de máximo V.
● Em qualquer caso, as coordenadas
● de V são:
● Xv = -b / 2*a
● Yv = -Delta / 4*a

8. Exercício 4: Identifique com base no estudo do vértice da
função quadrática, quais os valores do Xv e do Yv de cada
função
( ) h(x) = 7x² +x
( ) f(x) = -x² + 6x
( ) g(x) = (2-x)² + 3x + 5
( ) f(x) = - x + 8x² -9
( ) f(x) = x²
( ) f(x) = (2+x)²
( ) f(t) = 8 -9t + 5t²
( ) f(p) = p² - 4

9. Imagem da Função Quadrática
● A imagem da função y = ax² + bx + c, é o conjunto dos
valores que y pode assumir. Há duas possibilidades:
● 1ª - quando a > 0, 2ª - quando a < 0,
●
●

10. Exercício 5: Determine o conjunto imagem de cada função
tomando por base o valor do Yv encontrado na questão 4
( ) h(x) = 7x² +x
( ) f(x) = -x² + 6x
( ) g(x) = (2-x)² + 3x + 5
( ) f(x) = - x + 8x² -9
( ) f(x) = x²
( ) f(x) = (2+x)²
( ) f(t) = 8 -9t + 5t²
( ) f(p) = p² - 4

11. ●Construção da Gráfico
● É possível construir o gráfico de uma função do 2º grau
sem montar a tabela de pares (x, y), mas seguindo
apenas o roteiro de observação seguinte
● O valor do coeficiente a define a concavidade da parábola;
● Os zeros definem os pontos em que a parábola intercepta
o eixo dos x;
● O vértice V indica o ponto de mínimo (se a > 0), ou
máximo (se a< 0);
● A reta que passa por V e é paralela ao eixo dos y é o eixo
de simetria da parábola;
● Para x = 0 , temos y = a · 0²+ b · 0 + c = c; então (0, c) é o
ponto em que a parábola corta o eixo dos y.

12. Exercício 6: seguindo os passos descritos anteriormente
esboce o gráfico das funções a seguir.
( ) h(x) = 7x² +x
( ) f(x) = -x² + 6x
( ) g(x) = (2-x)² + 3x + 5
( ) f(x) = - x + 8x² -9
( ) f(x) = x²
( ) f(x) = (2+x)²
( ) f(t) = 8 -9t + 5t²
( ) f(p) = p² - 4

13. Estudo do Sinal da Parábola
● quando a > 0
●
● y > 0 (x < x1 ou x > x2)
● y < 0 x1 < x < x2
●
● quando a < 0
●
● y > 0 x1 < x < x2
● y < 0 (x < x1 ou x > x2)

14. Exercícios resolvidos
● Prova Resolvida PC MG 2008 – Acadepol – Questão 12. O
número de ocorrências registradas das 12 às 18 horas em
um dia do mês de janeiro, em uma delegacia do interior de
Minas Gerais, é dado por f(t) = – t² + 30t – 216, em que 12 ≤
t ≤ 18 é a hora desse dia. Pode-se afirmar que o número
máximo de ocorrências nesse período do dia foi
● A) 0
● B) 9
● C) 15
● D) 18

15. ●Prova Resolvida PC MG 2008 – Acadepol –
Questão 12
● Veja que a função f(t) = – t² + 30t – 216 é uma função do
segundo grau onde a parábola tem a concavidade para baixo (a
é menor que 0) Assim sendo, o t que faz a função ser máxima é
justamente o t do vértice, que pode ser calculado utilizando a
fórmula abaixo
● t(v) = -b/2a = -30/2(-1) = 15
● Logo, t = 15 horas foi o momento de maior número de
ocorrências.
●
Como já sabemos o momento de maior ocorrência, vamos
agora calcular t(15):
● t(15) = – 15² + 30.15 – 216 = -225 + 450 – 216 = 9 ocorrências.

16. ●Prova Resolvida CFO PM ES 2013 –
Exatus – Questão 68.
● Uma agência de viagens vende pacote turísticos coletivos com destino a
Fortaleza. Um pacote para 40 clientes custa R$ 2000,00 por pessoa e, em
caso de desistência, cada pessoa que permanecer no grupo deve pagar mais
R$ 100,00 por cada desistente do pacote de viagem. Dessa forma, para que
essa agência obtenha lucro máximo na venda desse pacote de viagens, o
número de pessoas que devem realizar a viagem é igual a:
● Repare que o preço total é dado pela quantidade de pessoas vezes o preço
por pessoa, que é 2000 mais 100 por desistente.
● C(x) = x(2000 + 100(40 – x))
● C(x) = x(2000 + 4000 – 100x)
● C(x) = x(6000 – 100x)
● C(x) = 6000x – 100x²
● Como em nossa função o valor de a = -100 < 0, o gráfico é uma parábola
para baixo, portanto possui valor máximo, e é exatamente o valor
correspondente ao Yv, e ocorre quando o X = Xv, o valor máximo ocorre
quando x = 30.

17. ●Prova Resolvida PM ES 2013 – Exatus –
Questão 53.
● Assinale a alternativa correta:
● a) O gráfico da função y = x² + 2x não intercepta o eixo y.
● FALSA: Uma parábola sempre intercepta o eixo y.
● b) O gráfico da função y = x² + 3x + 5 possui concavidade para baixo.
● FALSA: O valor de a = 1 >0. Concavidade para cima.
● c) O gráfico da função y = 5x – 7 é decrescente.
● FALSA: O valor de a = 5 > 0. Crescente.
● d) A equação x² + 25 = 0 possui duas raízes reais e diferentes.
● FALSA: Nenhum número Real elevado ao quadrado fica negativo.
● e) A soma das raízes da função y = x² – 3x – 10 é igual a 3.
● Verdadeira - Lembrando da fórmula da soma das raízes;
● Soma = ´-b/a = -(-3)/1 = 3

20. http://www.somatematica.com.br/
● Material de todos os assuntos de matemática nesta
página.
● http://sabermatematica.com.br/funcaoquadraticaer.html
● Exercícios de matemática resolvidos
● http://pt.slideshare.net/arthurprata/funo-do-segundo-grau
-caderno-de-atividades-enem-coc
● Questões do ENEM
●