O documento apresenta atividades sobre o uso de programas livres para o ensino de matemática e tecnologia. A primeira atividade aborda a resolução algébrica de sistemas de equações e a resolução gráfica através do programa Winplot. A segunda atividade trata da construção de um retângulo com área máxima de 96cm2 usando um barbante de 40cm e resolução algébrica e gráfica. A terceira atividade demonstra o teorema de Pitágoras usando a construção de um quadrado no programa C

1. Oficina: Semana da Matemática e Tecnologia no Ensino.
Atividades exemplos do uso de Programas livres
Atividade 01:
y = x

Resolva o sistema de equações 
y = x

Resolução ALGÉBRICA de sistemas de equações
Primeiramente, recordando-se por definição:
1. o módulo de x é tal que :  x, se x ≥ 0
x =
− x, se x < 0
2. o módulo de x é tal que :
x = x2
O que se pode deduzir partir da definição acima?
Que o valor absoluto de x nunca é negativo. Portanto, ele é sempre positivo ou zero.
Além, disso o que mais há de importante na resolução do exercício?
Uma das propriedades funadamentais do valor absoluto que é:
Dado que , x ≥0 é não negativo, então, 2
x = x 2 , ∀x ∈ R
Falta alguma coisa?
Sim. Lembrar que ∃y , y ∈ R, y = x ≥ 0 , ou seja, só existe raiz quadrada em IR se x for igual a zero ou
positivo.
Bem, agora se tem todo o referencial teórico necessário para a solução do exercício.
Passo1. Do sistema de equações basta igualá-las, obtendo-se :
x = x
Passo2. Aplica-se ao módulo de x, a definição 2, como x = x2 :
substituindo-se
x = x ⇒ x2 = x
x = x2
Passo3. Elimina-se a raiz quadrada, para isso, eleva-se ao quadrado ambos os membros da equação:
( x ) =( x )
2 2
2
⇔ x2 = x
Passo4. Soma-se a ambos os membros da equação o oposto de x, i.e., ( − x) obtém-se:
x 2 = x ⇒ x 2 + (− x) = x + (− x) ⇒ x 2 + (− x) = 0 ∴ x 2 − x = 0
2
Passo5. Como a equação é do 2º (ax +bx+c=0) e incompleta, ou seja, c=0, basta por em evidência x e ter-se-á
os dois valores soluções do sistema:
 x = 0 ⇒ y = 0 ∴ S1 = {( 0,1)}

x − x = 0 ⇒ x ( x − 1) = 0 ⇔ ou
2 Portanto, têm-se a solução S= {(0,0), (1,1)}.
 x = 1 ⇒ y = 1∴ S = { 1,1 }
 2 ( )

2. Resolução GRÁFICA através do programa
Passo1. Iniciar o programa Winplot, clicando em seu ícone.
Passo2. Fecha-se a janela de ajuda e abra-se o menu de janela
Passo3. Como as equações são em função das variáveis (x,y), ou seja ,logo, deveremos trabalhar em 2D, sendo
assim, devemos dar um clique em em 2-dim ou F2, e teremos o sistema de coordenadas ( x, y ) ∈ R 2 = R.R
∈ ∈
cartesianas que será nossa área de trabalho. R R
Passo4. Em seguida clica-se em Equação, abrindo-se um menu de ferramenta:

3. Passo5. Agora, com um clique em 1.Explícita, abrirá uma nova janela, onde digitaremos as 2 equações dadas
pelo exercício.
Passo6. Em seguida, preencha com os dados necessários Lembrando-se que em informática, não se esqueças
de colocar em parêntesis as variáveis e as potências nas equações
 y = f(x) = x : f(x) escreve-se x = abs(x)


 y = f(x) = x : f(x) escreve-se x = sqrt(x) ou (x)^(1/2)

Analogamente , para se obter y = f(x) = x
Passo7. Para finalizar cliques em Dois(sexta ferramenta da barra de menu)

4. Em seguida, cliques em Intersecções, depois marcar ponto e aparecerá um símbolo em cruz vermelha que será
a primeira solução (x1,y1)=(0,0), como há 2, cliques em próxima intersecção e obterás (x2,y2)=(1,1).
Tanto alunos como professores devem usá-lo não só em ensino fundamental ou médio, mas, também em ensino
superior, como ferramenta auxiliar. É um modo eficiente de validar a solução obtida através de resolução
algébrica ou analítica.

5. Atividade 02:
Dado um pedaço de barbante de 40 cm de comprimento, construa um retângulo com 96 cm² de área.
• Escreva uma equação que represente analiticamente a situação;
• desenhe o gráfico;
• qual é a área máxima?
• É possível atingir área maior que 100 cm²?
1. Resolução do primeiro item da questão
• Escreva uma equação que represente analiticamente a situação.
Como começar?
Primeiramente, esboçando-se as situações dadas pelo exercício, para isso, desenha-se a figura plana, retângulo,
nomeando-se seus lados. Sabe-se que |AB|=|CD| e |AD|=|BC| Em seguida, escolhem-se arbitrariamente duas
letras para designar os lados, por exemplo, (x, y).
E agora?
Escreve-se analiticamente a situação, lembrando-se que “o comprimento do barbante é igual ao perímetro do
retângulo”. Então, p= 2x + 2y = 40 cm, logo, vem que:
p = 40cm ⇒ 2x + 2y = 40 ⇔ 2 (x + y) = 2 (20) ∴ y + x = 20
O que mais se sabe dos dados do exercício?
2
Que a área do retângulo A = (base). (altura) = 96 cm , logo da geometria elementar, vem que: A = xy=>xy = 96.
Mas, há duas incógnitas (x, y) e agora?
Ora, como há duas incógnitas (x, y), então, é necessário eliminar uma, isto é fácil, basta isolar y da equação do
perímetro, assim, vem que:
y + x = 20 ⇔ y = 20 − x
Como prosseguir?
Substituindo-se o valor de y acima determinado na equação da área do retângulo, desse modo, obtém-se:
 y = 20 − x
(x, y) = (x,20 − x):  ⇒ A = xy ⇒ x(20 − x) = 96 ⇔ 20x − x 2 = 96
A = 96 cm
2
⇒ −96 + 20x − x 2 = 0 ∴ − x 2 + 20x − 96 = 0

6. 2. Resolução do segundo item da questão
• desenhe o gráfico
O que é necessário p/se fazer o gráfico da função do 2.º(quadrática)?
Primeiramente, lembre-se que a uma função é dada por: y = f(x). Além disso, a equação do 2.º grau tem a
seguinte forma: ax² + bx +c, c/ a<0.
Então, fazendo-se y = f(x) = ax² + bx +c, é necessário determinar as raízes, isto é, y = ax² + bx +c = 0,
prosseguindo-se, transforma-se a equação do 2.º grau é um quadrado perfeito, lembrando-se que:
2 2 2
(a + b) = a +2.a.b+b (Produto notável)
− x 2 + 20x − 96 = 0 ⇒ (−)(x 2 − 20x + 96) = 0 ⇒ x 2 − 20x + 96 = 0
⇒ x 2 − 20x + 96 = 0 ⇒ x 2 − 20x + 96 + (4) = 4
↓
100
⇒ x 2 − 20x + 100 = 4 ⇒ (x − 10) 2 = 4 ⇒ (x − 10) = ± 4
 x − 10 = +2  x1 = 12

⇒ (x − 10) = ±2 ⇔  ∴
 x − 10 = −2  x 2 = 8

O que falta?
Falta achar o vértice, para isso, acha-se o ponto médio entre as raízes e substitui o valor encontrado na equação
do 2.º grau (original) ou na fórmula para o cálculo de xv e yv.
x1 + x 2  x1 = 12
 12 + 8 20
x v = ?,sabe-se:x v = , mas  ⇒ xv = = ∴ x v = 10
2  x2 = 8
 2 2
y v = ?,sabe-se:y = x 2 − 20x + 96, mas, x v = 10 ⇒ y v = (10) 2 − 20(10) + 96
⇒ y v = 100 − 200 + 96 ⇒ y v = −4 ∴ ( x v , y v ) = (10, −4)
Mas y = ( −)(x 2 − 20x + 96) ∴ ( x v , y v ) = (10, 4)
O que mais se sabe?
Sabe-se que a função do 2.º tem como gráfico a parábola.
Além disso, y=f(x) = ax² + bx +c terá a concavidade voltada p/cima CVC (U) se a > 0(positivo) e a concavidade
voltada p/ baixo: CVB se a< 0(negativo).
Como y = f(x) = − x + 20x − 96 , como a = -1<0, o gráfico da parábola é voltado para baixo.
2
(x1, y1)= (oito, 0)
(x2, y2)= (12, 0)
(xv, yv) = (10, 4)
Importante :
o domínio da função na situação é D(f)=[8,12], i.e., 8 ≤ x ≤ 12 .
3. Resolução do terceiro item da questão
• qual é a área máxima?
O que se sabe sobre ÁREA máxima do retângulo?
Como a parábola atinge seu ponto máximo quando x =10, logo, a área máxima do retângulo, será:

7.  x = 10 
 y = 20 − x   ⇒ (x, y) = (10,10)
(x, y) = (x,20 − x):  ⇒  y = 20 − 10 = 10 
 A máx = ? A
 máx = ?
⇒ A máx = xy ⇒ A máx 10.10 ∴ A máx = 100 cm 2
Resposta: A área máxima é 100 cm², ela é atingida quando o retângulo é um quadrado de lados iguais a 10 cm.
4. Resolução do quarto item da questão
• É possível atingir área maior que 100 cm²?
Não. Porque ao se fazer uma tabela c/os pontos encontrados c/raízes, dando a “x” o maior valor e a “y”, o menor,
prossegue-se, decrescendo x e crescendo y e até que “x” atinja o menor valor e “y”, o maior. A cada ponto
obtido, efetuam-se o produto entre eles, determinando assim as áreas dos retângulos. Obteremos:
(x1, y1)= (12, 8) =>A1=12. 8 = 96 cm²
(x2, y2) = (11, 9) =>A2=11. 9 = 99 cm2
(x3, y3)= (10, 10) => A3=10.10 = 100 cm²
2
(x4, y4) = (9, 11) =>A4=9.11 = 99 cm
2
(x4, y4) = (8, 12) =>A4=9.11 = 99 cm .
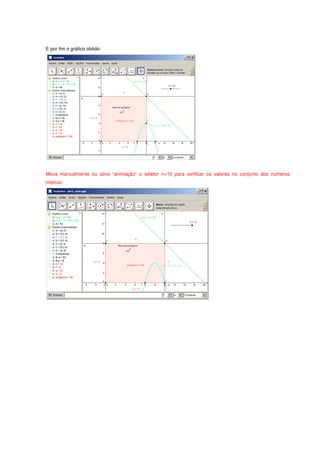
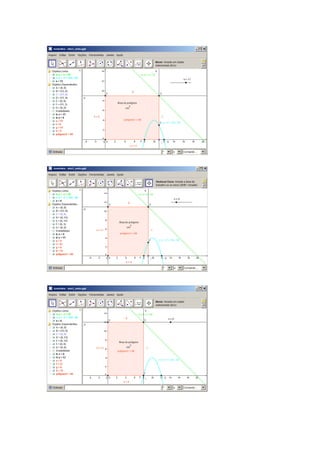
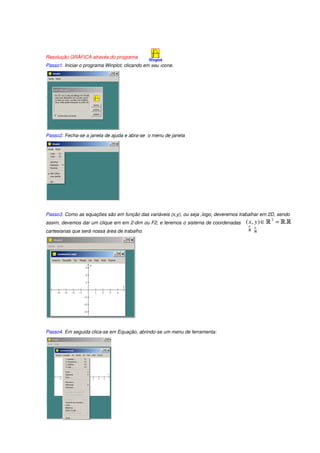
Resolução GRÁFICA através do programa
Observe o protocolo de construção, contendo 14 passos. Basta segui-los para obter a solução do exercício.
Antes disso, é importante fazer os seguintes procedimentos na janela do seletor, definir o intervalo (Max, Mín.) =
[8,12] e incremento com o valor igual à unidade:
Agora, temos o protocolo de construção:

8. E por fim o gráfico obtido:
Mova manualmente ou ative “animação” o seletor n=10 para verificar os valores no conjunto dos números
inteiros:

10. Atividade 03
Construa um triângulo retângulo qualquer e demonstre o teorema de Pitágoras usando a construção macro do
polígono quadrado.
Qual é o referencial teórico?
É o teorema de Pitágoras diz que: “Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é
igual à soma dos quadrados das medidas dos catetos”.
Agora constrói-se em C.a.R. um quadrado
Em seguida, usa-se a ferramenta “Ocultar Objeto”, a fim de deixar somente a figura do quadrado:

11. Após ocultar as construções que determinaram o quadrado, clique em macro:
Perceba que o ícone da ferramenta macro mudou de para . Agora, definem-se os parâmetros iniciais
da construção do quadrado pontos A e B e segmento AB. Em seguida, clica-se novamente em e volta na
figura para clicar nos segmentos AB, BC, CD e DA e na figura do polígono, i.e., dentro do polígono. Feito isso,
clique em e abrirá a seguinte janela e preencha tal qual a figura abaixo:
Depois aperte Ok para salvar macro do quadrado.
Em seguida, construa o triângulo retângulo FÊG, reto em E.

12. Use a ferramenta “Oculta Objeto” para esconder a reta perpendicular usada na construção do triângulo
retângulo. Em seguida, clica-se com o botão direito do mouse sobre o segmento EF e abrirá uma janela, nela
selecione os botões e . Tal qual a figura abaixo:
Dê “OK”, e faças analogamente ao segmento FG e EG, para obter os valores das medidas desses segmentos.
Para usar macro, clica-se no botão “Executar Macro”:
Abrirá à janela, “Escolha”, selecione “quadrado” e clique em “OK”:

13. Para finalizar, basta clicar em dois pontos de cada um dos segmentos que formam os lados do triângulo
retângulo FÊG e obteremos os respectivos quadrados a esses lados, provando desse modo à validade do
teorema de Pitágoras.
A fim de obter os quadrados das medidas dos lados do triangulo retângulo, clica-se em “Expressão Aritmética”.
Portanto, abrirá a janela “Editar Expressão”, preencha-a tal qual modelo abaixo a cada um dos segmentos do
triângulo:
Obtendo-se assim, a figura a seguir:

14. Para verificar a validade do Teorema de Pitágoras, mova qualquer um dos pontos do triângulo FÊG.