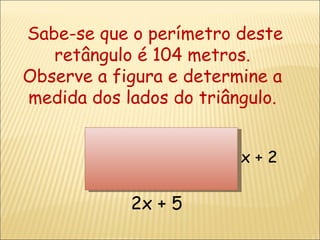
1) O documento apresenta exemplos de resolução de problemas envolvendo equações do 1o grau com uma incógnita. 2) As etapas para resolver problemas são: ler o problema, escrever dados, equação e resolver a equação. 3) Os exemplos incluem problemas sobre idades de pessoas, coleções de selos e comprimento de uma pista de corrida.

1. “ Felizes aqueles que se divertem com problemas que educam a alma e elevam o espírito.” Fenelon

2. Resolução de Problemas envolvendo Equações do 1º Grau com uma Incógnita

3. Para resolver uma situação-problema, devemos:

5. A soma das idades de André e Carlos é 22 anos. Descubra as idades de cada um deles, sabendo-se que André é 4 anos mais novo do que Carlos.

6. Dados do problema: Idade de André: x - 4 Idade de Carlos: x Soma das idades: 22 anos Equação do Problema: (x – 4) + x = 22

7. Resolução da Equação: (x – 4) + x = 22 x – 4 + x = 22 x + x = 22 + 4 2x = 26 x = 26/2 x = 13 Resposta: Carlos tem 13 anos e André tem 9 anos

8. Emílio e Guilherme colecionam selos. A coleção de Emílio tem 12 vezes o que tem a coleção de Guilherme. Se cada um ganhar 225 selos, Emílio terá o triplo do que terá Guilherme. Quantos selos cada um possui?

9. Dados do problema: Guilherme: x Emílio: 12x Guilherme: x + 225 Emílio: 12x + 225 Equação: 3(x + 225) = 12x + 225

11. Victor pratica ciclismo em uma pista de circuito fechado com extensão de 400 metros mais um trecho de comprimento desconhecido. Victor deu 10 voltas e o mostrador de distância percorrida indicou 10 km. Em metros, qual é o comprimento do trecho de comprimento desconhecido?

12. Dados do problema: Comp. desconhecido da pista: x Comp. total da pista: 400 + x Dist. Percorrida: 10 km = 1000m Equação do problema: 10(400 + x) = 10000

13. Resolução da Equação: 10(400 + x) = 10000 4000 + 10x = 10000 10x = 10000 – 4000 10x = 6000 x = 6000/10 x = 600 Resp.: O comprimento do trecho desconhecido é 600 metros.

14. Sabe-se que o perímetro deste retângulo é 104 metros. Observe a figura e determine a medida dos lados do triângulo. 2x + 5 x + 2

15. Dados do problema: Base: 2x + 5 Altura: x + 2 Perímetro: 104 metros Equação do problema: 2(2x + 5) + 2(x + 2) = 104

16. Resolução da Equação: 2(2x + 5) + 2(x + 2) = 104 4x + 10 + 2x + 4 = 104 4x + 2x = 104 – 10 – 4 6x = 90 x = 90/6 x = 15

17. Resposta: Base: 2x + 5 = 2.(15) + 5 = 30 + 5 = 35 metros Altura: (15) + 2 = 17 metros A base mede 35 metros e a altura mede 17 metros

18. PROFESSORA: Rita Medrado