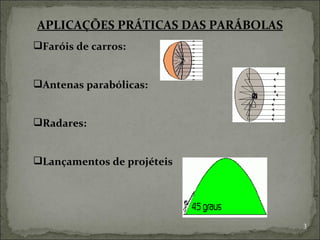
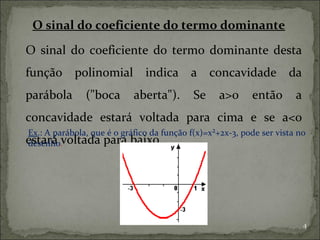
O documento discute equações do segundo grau e parábolas, incluindo suas aplicações, propriedades e como construí-las. Explica como determinar vértices, raízes, máximos e mínimos, e relaciona essas características com os coeficientes da equação. Por fim, fornece exercícios para praticar os conceitos aprendidos.

1. 1

2. representa uma equação trinômia do
segundo grau ou simplesmente uma
equação do segundo grau. O gráfico
cartesiano desta função polinomial do
segundo grau é uma curva plana
denominada parábola.
2

3. APLICAÇÕES PRÁTICAS DAS PARÁBOLAS
Faróis de carros:
Antenas parabólicas:
Radares:
Lançamentos de projéteis
3

4. O sinal do coeficiente do termo dominante
O sinal do coeficiente do termo dominante desta
função polinomial indica a concavidade da
parábola ("boca aberta"). Se a>0 então a
concavidade estará voltada para cima e se a<0
Ex.: A parábola, que é o gráfico da função f(x)=x²+2x-3, pode ser vista no
estará .voltada para baixo.
desenho
4

5. Para construir esta parábola dá-se valores para x
e obtém-se os respectivos valores para f(x). A
tabela a seguir mostra alguns pares ordenados
de pontos do plano cartesiano onde a curva
deverá passar:
x -3 -2 -1 0 1 2
y 0 -3 -4 -3 0 5
Como a>0, a concavidade ("boca") da nossa
parábola estará voltada para cima.
5

6. Relacionamento entre o discriminante e a concavidade
Podemos construir uma tabela que relaciona o sinal do
discriminante com o sinal do coeficiente do termo dominante
da função polinomial.
a > 0 concavidade (boca) para cima
a < 0 concavidade (boca) para baixo
D > 0,a parábola corta o eixo x em dois pontos diferentes.
D = 0 ,a parábola corta o eixo x num único ponto.
D < 0, a parábola não corta o eixo x.
6

7. Máximos e mínimos com funções quadráticas
Existem muitas aplicações para a função quadrática e uma delas
está relacionada com a questão de máximos e mínimos.
Exemplo: Determinar o retângulo de maior área que é
possível construir se o seu perímetro mede 36 m.
Solução: Se x é a medida do comprimento e y é a
medida da largura, a área será dada por: A(x,y)=xy,
mas acontece que 2x+2y=36 ou seja x+y=18, assim:
A(x) = x(18-x)
7

8. Esta parábola corta o eixo OX nos pontos
x=0 e x=18 e o ponto de máximo dessa
curva ocorre no ponto médio entre x=0 e
x=18, logo, o ponto de máximo desta curva
ocorre em x=9.
Observamos que este não é um retângulo
qualquer mas é um quadrado pois x=y=9 e a
área máxima será A=81m²
8

9. Exercícios
1.Construir o gráfico cartesiano de cada uma das
funções do segundo grau:
a) f(x) = x²-3x-4
b) f(x) = -3x²+5x-8
c) f(x) = 4x²-4x+1
9

10. Coordenadas do vértice
A coordenada x do vértice da parábola
pode ser determinada por .
Exemplo: Determine as coordenadas do
vértice da parábola y = x²-4x + 3
Temos: a=1, b=-4 e c=3
10

11. Logo, a coordenada x será igual a 2, mas e a
coordenada y?
Simples: Vamos substituir o valor obtido da
coordenada x e determinar o valor da coordenada y.
Assim, para determinarmos a coordenada y da
parábola
y=x²-4x+3, devemos substituir o valor de x por 2.
y = (2)²-4.(2)+3 = 4-8+3=-1
Logo, as coordenadas do vértice serão V=(2,-1)
11

12. Raízes (ou zeros) da função do 2º
grau
Denominam-se raízes da função do 2º
grau os valores de x para os quais ela se
anula.
y=f(x)=0
Exemplo: na função y=x²-4x+3, que acima
acabamos de determinar as coordenadas
de seus vértices, as raízes da função
serão x=1 e x` = 3.
12

13. Como determinar a raiz ou zero da função do
2º grau?
Aplicando a resolução de equações do 2º
grau, já vista na seção anterior.
Exemplo: determine a raiz da função
y=x²+5x+6:
Fazendo y=f(x)=0, temos x²+5x+6=0
Agora basta resolver a equação aplicando a
fórmula de Bháskara.
x²+5x+6=0
13

14. Acharemos que x = -2 e x`= -3.
14

15. Concavidade da parábola
Quando a>0, a concavidade da
parábola está voltada para cima
(carinha feliz) e quando a<0, a parábola
está voltada para baixo (carinha
triste).
15

16. Quando o discriminante é igual a
zero
Quando o valor de , o vértice a
parábola encontra-se no eixo x. A coordenada y
será igual a zero.
Exemplo: y=f(x)=x²+2x+1
x²+2x+1=0
x = x` = -b/2a =-1
As coordenadas do vértice serão V=(-1,0)
16

17. Exercícios de aprendizagem
3)Encontre o vértice, o eixo de simetria do gráfico , a
imagem de cada uma das funções. Classifique o vértice
como um ponto de máximo ou de mínimo da função
dada.
17

18. 2.Esboce o gráfico e determine o domínio e o conjunto-
imagem de cada função abaixo:
a) y= x² - 2x – 3
b) y= -4x² + 8x
c) y= 2x² -2x + 1
d) y= x² -2x + 1
e) y= -x² -9
3.Esboce o gráfico e determine o valor máximo (ou mínimo) e o
ponto de máximo (ou o de mínimo) de cada função abaixo:
a) y= x² -8x+7
b) y= -2x² + 2x -3
c) y= -x² + 2x +8
d) y= 3x² -2x +1
18

19. 4.Discuta a variação de sinal das funções abaixo:
a) f(x)= x² -5x + 4
b) f(x)= -x² + x + 2
c) Y= x²/2 – x + ½
d) f(x)= -x² + 6x -9
e) f(x) = 3x² -x +1
f) f(x)= -2x²/3+ x – 4/3
5.Dada a função f(x)=x²-5x+6,calcule:
c)f(1)
d)f(-1)
e)f(2)
f)f(-1/2)
g)f(0)
h)f(3)
19

20. 6. Dada a função f(x)= x² -4x -5, determine os valores reais
de x para que se tenha:
a) f(x)= 7
b) f(x)= 0
c) f(x)= -5
7. Calcule K de modo que a função y= kx² -2x + 3 admita 2
como zero.
8.Dada a função f(x)= ax² + bx + 10, calcule a e b
sabendo que suas raízes são -2 e 5.
9.Determine V(xv; yv),vértices da parábola das seguintes
funções:
b)y= x² - 6x + 5
c)y=3x² -2x + 2
d)y= x² -x -2
e)y= x² - 4
20