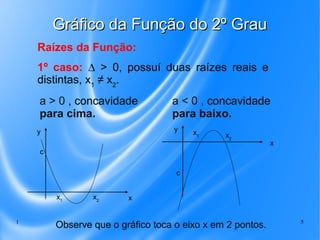
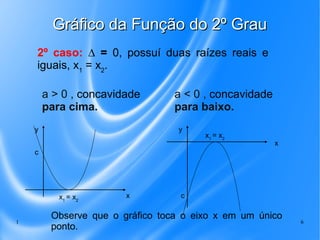
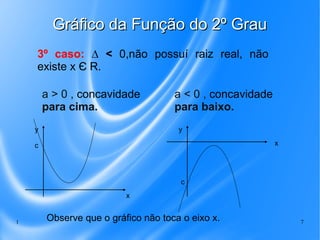
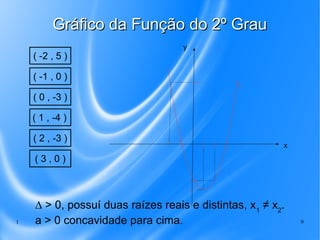
Este documento discute o gráfico da função do segundo grau. Explica que o gráfico é uma parábola e que a concavidade depende do sinal do coeficiente a. Também descreve os três casos possíveis para as raízes de acordo com o valor de Δ e ilustra a construção do gráfico atribuindo valores a x.

1. 1 1
Matemática
Gráfico da Função do 2º Grau
Prof. Roberto
Visite meu blog:
www.betontem.blogspot.com.br

2. 1 2
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
Concavidade:
O gráfico de uma função quadrática, é
representado por uma curva denominada
parábola.
Em relação à concavidade, a parábola que
representa uma função quadrática, pode ser
voltada para cima ou para baixo.

3. 1 3
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
Dada a função f(x) = ax² + bx + c, cujo gráfico é uma
parábola, se:
a > 0 , o coeficiente a é positivo a concavidade da
parábola é voltada para cima.
y
x

4. 1 4
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
a < 0 , o coeficiente a é negativo a concavidade da
parábola é voltada para baixo.
y
x

5. 1 5
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
1º caso: ∆ > 0, possuí duas raízes reais e
distintas, x1
≠ x2
.
Raízes da Função:
a > 0 , concavidade
para cima.
xx1
x2
y
a < 0 , concavidade
para baixo.
x
x1 x2
y
c
c
Observe que o gráfico toca o eixo x em 2 pontos.

6. 1 6
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
2º caso: ∆ = 0, possuí duas raízes reais e
iguais, x1
= x2
.
a > 0 , concavidade
para cima.
xx1
= x2
y
a < 0 , concavidade
para baixo.
x
y
c
c
x1
= x2
Observe que o gráfico toca o eixo x em um único
ponto.

7. 1 7
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
3º caso: ∆ < 0,não possuí raiz real, não
existe x Є R.
a > 0 , concavidade
para cima.
x
y
a < 0 , concavidade
para baixo.
x
y
c
c
Observe que o gráfico não toca o eixo x.

8. 1 8
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
Gráfico da função:
Para construirmos o gráfico de uma função do 2º
grau, procedemos do seguinte modo.
a) y = x² - 2x - 3
x y
-2 (-2)² – 2.(-2) - 3 5
x² – 2x - 3 (x,y)
( -2 , 5 )
-1 (-1)² – 2.(-1) - 3 0 ( -1 , 0 )
0 0² – 2 . 0 - 3 -3 ( 0 , -3 )
1 1² – 2.1 - 3 -4 ( 1 , -4 )
2 2² – 2.2 - 3 -3 ( 2 , -3 )
3 3² – 2.3 - 3 0 ( 3 , 0 )
Atribuímos valores
a x e obtemos os
pares ordenados.

9. 1 9
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
x
y
( -2 , 5 )
( -1 , 0 )
( 0 , -3 )
( 1 , -4 )
( 2 , -3 )
( 3 , 0 )
∆ > 0, possuí duas raízes reais e distintas, x1
≠ x2
.
a > 0 concavidade para cima.

10. 1 10
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
b) y = -x² + 2x -4
x y-x² + 2x - 4 (x,y)
-1 -(-1)² + 2.(-1) - 4 -7 ( -1 , -7 )
0 0² + 2 . 0 - 4 -4 ( 0 , -4 )
1 -(1)² + 2.1 - 4 -3 ( 1 , -3 )
2 -(2)² + 2.2 - 4 -4 ( 2 , -4 )
3 -(3)² + 2.3 - 4 -7 ( 3 , -7 )
Atribuímos valores
a x e obtemos os
pares ordenados.

11. 1 11
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
x
y
( -1 , -7 )
( 0 , -4 )
( 1 , -3 )
( 2 , -4 )
( 3 , -7 )
∆ < 0,não possuí raiz real, não existe x Є R.
a < 0 concavidade para baixo.

12. 1 12
Gráfico da Função do 2º GrauGráfico da Função do 2º Grau
ATENÇÃO:
O gráfico de uma função quadrática (função
do 2º grau) é uma curva aberta chamada
parábola.

13. 1 13
Atividade elaborada pelo:
Prof. Roberto
Disciplina Matemática.
Visite meu blog:
www.betontem.blogspot.com.br

14. 1 14
REFERÊNCIAS BIBLIOGRÁFICAS:
BOSQUILHA, Alessandra – CORRÊA, Marlene L. Pires –
VIVEIRO, Tânia Cristina Neto G. - Mini Manual Compacto
de Matemática Ensino Médio: Editora Rideel.
GIOVANNI, José Ruy – BONJORNO, José Roberto –
GIOVANNI JR., José Ruy. - Matemática Completa: Editora
FTD..