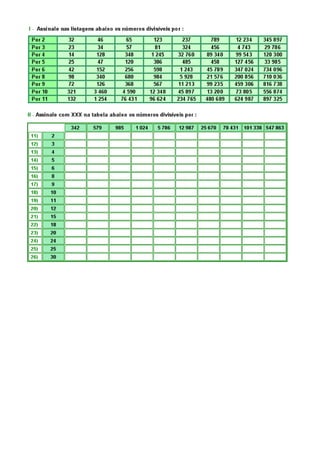
O documento explica os conceitos básicos de divisibilidade, como determinar se um número é divisível por outro através de critérios como a soma dos algarismos ou os algarismos das unidades. Além disso, apresenta os principais critérios de divisibilidade para números de 2 a 11, permitindo verificar a divisibilidade mentalmente.

1. Divisibilidade
Um número N é divisível por um número p quando a divisão de N por p der como quociente um número
natural e 0 para resto.
Sendo assim, N é divisível por p. E com isso diremos que N é múltiplo de p, e p é divisor de N.
Exemplos :
21 é divisível por 3, já que 21 : 3 tem 7 por quociente e o resto 0. Com isso: 21 é múltiplo de 3 e 3 é divisor
de 21
125 é divisível por 5, já que 125 : 5 dá 25 para quociente e o resto 0. Com isso: 125 é múltiplo de 5 e 5 é
divisor de 125
327 não é divisível por 11, já que 327 : 11 dá para quociente 29 e o resto 8. Com isso: 327 não é múltiplo
de 11 e 11 não é divisor de 11
Critérios de Divisibilidade
Em muitas situações precisamos apenas descobrir se um número é divisível por outro, sem a
necessidade de sabermos o quociente
da divisão entre eles. Neste caso utilizamos alguns mecanismos ou regras conhecidas como critérios de
divisibilidade.
Os Principais Critérios de Divisibilidade
Divisibilidade por 2
Um número é divisível por 2 quando o algarismo das unidades for 0, 2, 4, 6 ou 8.
Assim sendo: um número é divisível por 2 quando ele for par.
Exemplos :
124 é divisível por 2, já que o algarismo das unidades é 4. Com isso: 124 é divisível por 2, 124 é múltiplo
de 2 e 2 é divisor de 124
1258 é divisível por 2, já que o algarismo das unidades é 8. Com isso: 1258 é divisível por 2, 1258 é
múltiplo de 2 e 2 é divisor de 1258
3275 não é divisível por 2, já que o algarismo das unidades é 5. Com isso: 3275 não é divisível por 2,
3275 não é múltiplo de 2 e 2 não é
divisor de 3275
A partir daqui chamaremos Critério de Divisibilidade apenas por Divisibilidade
Divisibilidade por 3
Um número é divisível por 3 quando a soma de seus algarismos gerar um múltiplo de 3.
Exemplos :
138 é divisível por 3, já que 1 + 3 + 8 = 12, e 12 é um múltiplo de 3. Com isso: 138 é divisível por 3, 138 é
múltiplo de 3 e 3 é divisor de

2. 138
3821 não é divisível por 3, já que 3 + 8 + 2 + 1 = 14, e 14 não é um múltiplo de 3. Com isso: 3821 não é
divisível por 3, 3821 não é
múltiplo de 3 e 3 não é divisor de 3821
8973 é divisível por 3, já que 8 + 9 + 7 + 3 = 27, e 27 é um múltiplo de 3. Com isso: 8973 é divisível por 3,
8973 é múltiplo de 3 e 3 é
divisor de 8973
Divisibilidade por 4 - Critério 1
Um número é divisível por 4 quando o número formado pelos dois últimos algarismos da direita der um
múltiplo de 4.
Exemplos :
128 é divisível por 4, já que o número 28 é um múltiplo de 4. Com isso: 128 é divisível por 4, 128 é
múltiplo de 4 e 4 é divisor de 128
2132 é divisível por 4, já que o número 32 é um múltiplo de 4. Com isso: 2132 é divisível por 4, 2132 é
múltiplo de 4 e 4 é divisor de 3821
5946 não é divisível por 4, já que o número 46 não é um múltiplo de 4Com isso: 5946 não é divisível por 4,
5946 não é múltiplo de 4 e
4 não é divisor de 5946
Divisibilidade por 4 - Critério 2
Um número é divisível por 4 quando o dobro do algarismo das dezenas adicionado ao algarismo das
unidades gerar um
múltiplo de 4.
Exemplos :
124 é divisível por 4, já que: 2 X 2 + 4 = 8, e 8 é um múltiplo de 4. Com isso: 124 é divisível por 4, 124 é
múltiplo de 4 e 4 é divisor
de 124
38543 não é divisível por 4, já que: 4 X 2 + 3 = 11, e 11 não é um múltiplo de 4. Com isso: 38543 não é
divisível por 4, 38543 não é
múltiplo de 4 e 4 não é divisor de 38543
Observação Importante: Um número N somente será divisível por 4 se ele for um número par. Sendo N
um número ímpar nem se faz
necessária a verificação já que de antemão ele não será divisível por 4.
Divisibilidade por 5
Um número é divisível por 5 quando seu algarismo das unidades for 0 ou 5.
Exemplos :
245 é divisível por 5, já que termina em 5. Com isso: 245 é divisível por 5, 245 é múltiplo de 5 e 5 é divisor
de 245
3040 é divisível por 5, já que termina em 0. Com isso: 3040 é divisível por 5, 3040 é múltiplo de 5 e 5 é
divisor de 3040

3. 23 457 não é divisível por 5, já que não termina em 0 ou 5. Com isso: 23 457 não é divisível por 5, 23 457
não é múltiplo de 5 e
5 não é divisor de 23 457
Divisibilidade por 6
Um número somente é divisível por 6 quando for par e a soma de seus algarismos for um número
divisível por 3. Ou seja, um número é
divisível por 6 quando for, simultaneamente, divisível por 2 e por 3.
Divisibilidade por 6 - Método Exclusivo
Um número é divisível por 6 quando o algarismo das unidades, adicionado ao quádruplo da soma dos
demais algarismos, der um
número divisível por 6. Se o número obtido ainda possuir uma grande quantidade de algarismos, repete-
se o processo até que se
possa verificar mentalmente a divisão por 6.
Exemplo 1: 164 928 é divisível por 6 ? Verifiquemos:
8 Algarismo das Unidades
Quádruplo da Soma dos Demais
4 (1+ 6 + 4 + 9 + 2 )= 88
Algarismos
8 + 88 = 96 Soma
Repetindo o processo para o Número 96
6 Algarismo das Unidades
Quádruplo da Soma dos Demais
4X9
Algarismos
6 + 36 = 42 Soma
O Resultado soma 42 é um múltiplo de 6, portanto o número original 164928 é divisível por 6.
Exemplo 2: 1.875.392 é divisível por 6 ? Verifiquemos:
2 Algarismo das Unidades
4 (1+ 8 + 7 + 5 + 3 + 9 ) = Quádruplo da Soma dos Demais
132 Algarismos
2 + 132 = 134 Soma
Repetindo o processo para o Número 134
4 Algarismo das Unidades
Quádruplo da Soma dos Demais
4 x ( 1 + 3 ) = 16
Algarismos
4 + 16 = 20 Soma

4. O Resultado soma 20 não é um múltiplo de 6, portanto o número original 1.875.392 não é divisível por 6
Divisibilidade por 7
Devido à complexidade desse critério e dele não constar no programa do ensino fundamental não o
estudaremos nesse capítulo.
Divisibilidade por 8 - Critério 1
Um número é divisível por 8 quando o número formado pelos três últimos algarismos da direita formar
um múltiplo de 8.
Exemplos :
5 432 é divisível por 8, já que o número 432 é um múltiplo de 8. Com isso: 5 432 é divisível por 8, 5 432 é
múltiplo de 8 e 8 é divisor de
5 432
72 152 é divisível por 8, já que o número 152 é um múltiplo de 8. Com isso: 72 152 é divisível por 8, 72
152 é múltiplo de 8 e
8 é divisor de 72 152
35 946 não é divisível por 8, já que o número 946 não é um múltiplo de 8. Com isso: 35 946 não é divisível
por 8, 35 946 não é múltiplo
de 8 e 8 não é divisor de 35 946
Divisibilidade por 8 - Critério 2
Um número é divisível por 8 quando o quádruplo do algarismo das centenas adicionado ao dobro do
algarismo das dezenas e
adicionado ao algarismo das unidades der um múltiplo de 8.
Exemplos :
3 128 é divisível por 8, já que: 4 X 1 + 2 X 2 + 8 = 16, e 16 é um múltiplo de 4. Com isso: 3 128 é divisível
por 8, 3 128 é múltiplo de 8 e
8 é divisor de 3 128
38 542 não é divisível por 8, já que: 4 X 5 + 2 X 4 + 2 = 30, e 30 não é um múltiplo de 8. Com isso: 38 542
não é divisível por 8, 38 542
não é múltiplo de 8 e 8 não é divisor de 38 542
Observação Importante: Um número N somente será divisível por 8 se ele for um número par. Sendo N
um o número ímpar nem se
faz necessária a verificação já que de antemão ele não será divisível por 8.
Divisibilidade por 9
Um número é divisível por 9 quando a soma de seus algarismos der um múltiplo de 9.
Exemplos :
234 é divisível por 3, já que 2 + 3 + 4 = 9, e 9 é um múltiplo de 9. Com isso: 234 é divisível por 9, 234 é

5. múltiplo de 9 e
9 é divisor de 234
5 723 não é divisível por 9, já que 5 + 7 + 2 + 3 = 17, e 17 não é um múltiplo de 9.
Com isso: 5 723 não é divisível por 3, 5 723 não é múltiplo de 9 e 9 não é divisor de 5 723
6 975 é divisível por 9, já que 6 + 9 + 7 + 5 = 27, e 27 é um múltiplo de 9. Com isso: 6 975 é divisível por 3,
6 975 é múltiplo de 9 e
9 é divisor de 6 975.
Divisibilidade por 10
Um número é divisível por 10 quando seu algarismo das unidades for 0.
Exemplos :
240 é divisível por 10, já que 240 termina em 0. Com isso: 240 é divisível por 10, 240 é múltiplo de 10 e 10
é divisor de 240
3 040 é divisível por 10, já que 3 040 termina em 0. Com isso: 3 040 é divisível por 10, 3 040 é múltiplo de
10 e 10 é divisor de
3 040
63 587 não é divisível por 10, já que não termina em 0. Com isso: 63 587 não é divisível por 10, 63 587
não é múltiplo de 10 e
10 não é divisor de 63 587
Divisibilidade por 11
Um número é divisível por 11 quando a soma dos algarismos de ordem ímpar Si diminuída da soma dos
algarismos de
ordem ímpar Sp for um número inteiro divisível por 11.
Expliquemos inicialmente o que é ordem ímpar e ordem par em um número.
Seja por exemplo o numero 125 796, sabemos que ele tem seis ordens. O algarismo 6 ocupa a primeira
ordem, o algarismo 7 ocupa a
terceira ordem e o algarismo 2 ocupa a quinta ordem - Esses são os algarismos de ordem ímpar. ( Si )
Da mesma forma que:
O algarismo 9 ocupa a segunda ordem, o algarismo 5 ocupa a quarta ordem e o algarismo 1 ocupa a
sexta ordem -
Esses são os algarismos de ordem par. ( Sp )
Ou seja: Não importa se o algarismo é par ou ímpar, o que importa é a posição que ele ocupa no número.

6. Divisibilidade por Números Múltiplos
Exercícios Propostos

9. Respostas dos Exercícios Propostos
Matemática Muito Fácil - Aritmética - Divisibilidade