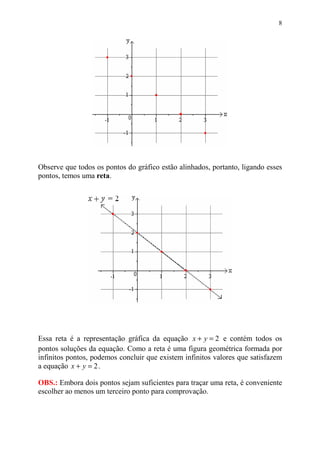
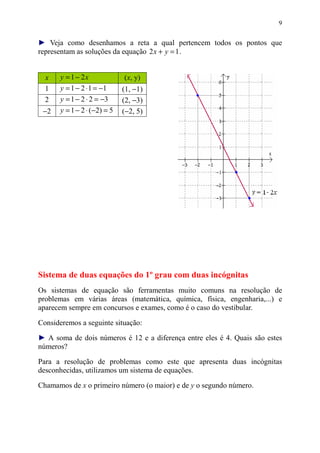
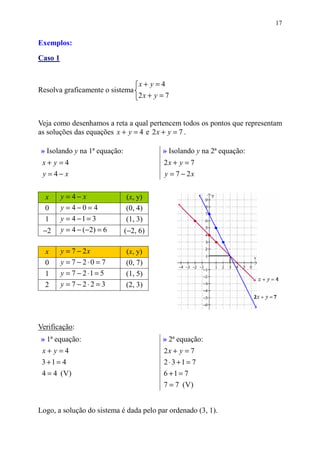
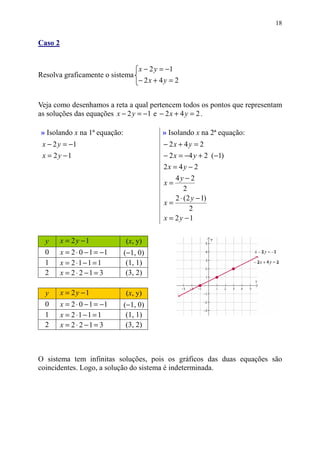
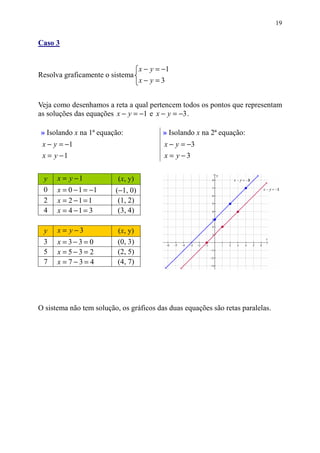
Este documento discute equações de primeiro grau com duas incógnitas, como encontrar soluções para tais equações, e representá-las graficamente em um plano cartesiano. Explica como cada solução é um par ordenado (x, y) e como atribuir valores a uma das variáveis calcula o valor da outra.

1. Equações do 1º grau
(Parte 4)
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
Equações do 1º grau com duas incógnitas ...................................................................... 1
Solução de uma equação do 1º grau com duas incógnitas ....................................... 2
Par ordenado e plano cartesiano ..................................................................................... 6
Gráfico da equação ax + by = c....................................................................................... 7
Sistema de duas equações do 1º grau com duas incógnitas ............................................ 9
Solução de um sistema de duas equações do 1º grau com duas incógnitas ................10
Método da substituição ....................................................................................... 11
Método da comparação ....................................................................................... 12
Método da adição................................................................................................ 14
Representação gráfica de um sistema de duas equações do 1º grau com duas
incógnitas................................................................................................................ 16
Referências bibliográficas............................................................................................. 20
"Sempre que desconheceres algo, chama-o de x e empenha-te em
investigá-lo" (Albert Einstein)

2. 1
EQUAÇÕES DO 1º GRAU
Equações do 1º grau com duas incógnitas
Observe esta situação:
► Uma equipe de basquete disputa, em um torneio, 4 jogos. No quadro
seguinte, vamos colocar todas as possibilidades de vitórias e de derrotas dessa
equipe no torneio:
Vitórias Derrotas Partidas disputadas
4 0 4+0=4
3 1 3+1=4
2 2 2+2=4
1 3 1+3=4
0 4 0+4=4
Indicando-se pela letra x o possível número de vitórias e pela letra y o possível
número de derrotas, a sentença “Uma equipe de basquete disputa, em um
torneio, 4 jogos” pode ser representada pela sentença matemática:
x+ y=4
Essa sentença matemática é chamada equação do 1º grau com duas incógnitas.
Assim, podemos afirmar:
Toda equação que pode ser reduzida a uma equivalente da forma ax + by = c ,
com a ≠ 0 e b ≠ 0 , denomina-se equação do 1º grau com duas incógnitas, x e y.
Exemplos de equações de 1º grau com duas incógnitas:
a) x + y = 23
b) x − y = 19
c) 3 x + y = 7
d) 2 x − 3 y = 31

3. 2
Solução de uma equação do 1º grau com duas incógnitas
► Considerando a equação 2 x + 5 y = 16 , quais devem ser os valores dos
números x e y para que a igualdade seja verdadeira?
Observe:
a) Se atribuirmos a x o valor 3 e a y o valor 2, teremos:
2 x + 5 y = 16
2 ⋅ 3 + 5 ⋅ 2 = 16
6 + 10 = 16
16 = 16 → a igualdade é verdadeira
b) Considerando a x = −2 e y = 4 , teremos:
2 x + 5 y = 16
2 ⋅ (−2) + 5 ⋅ 4 = 16
− 4 + 20 = 16
16 = 16 → a igualdade é verdadeira
1
c) Considerando a x = e y = 3 , teremos:
2
2 x + 5 y = 16
1
2 ⋅ + 5 ⋅ 3 = 16
2
1 + 15 = 16
16 = 16 → a igualdade é verdadeira
d) Considerando a x = 4 e y = 1 , teremos:
2 x + 5 y = 16
2 ⋅ 4 + 5 ⋅ 1 = 16
8 + 5 = 16
13 = 16 → a igualdade não é verdadeira, pois 13 ≠ 16

4. 3
2
e) Considerando a x = −4 e y = , teremos:
5
2 x + 5 y = 16
2
2 ⋅ (−4) + 5 ⋅ = 16
5
− 8 + 2 = 16
− 6 = 16 → a igualdade não é verdadeira, pois − 6 ≠ 16
Através do que foi visto, você notou que existem vários pares de números que
tornam verdadeira a equação:
• x=3 e y=2
• x = −2 e y = 4
1
• x= e y=3
2
Todos esses pares de valores são soluções da equação 2 x + 5 y = 16 . Os outros
pares não são soluções da equação dada.
Então:
Uma equação do 1º grau com duas incógnitas tem infinitas soluções. Cada
solução da equação é um par ordenado de números: o primeiro número
representa sempre o valor de x, enquanto o segundo representa sempre o valor
de y. Daí o nome par ordenado. Indica-se: (x, y).
Assim:
• O par de valores formado por x = 3 e y = 2 é uma solução da equação
2 x + 5 y = 16 . Essa solução pode ser indicada por (3, 2).
• O par de valores formado por x = −2 e y = 4 é uma solução da equação
2 x + 5 y = 16 . Essa solução pode ser indicada por (−2, 4).
1
• O par de valores formado por x = e y = 3 é uma solução da equação
2
1 
2 x + 5 y = 16 . Essa solução pode ser indicada por  , 3  .
2 

5. 4
As soluções de uma equação do 1º grau com duas variáveis podem ser
encontradas atribuindo-se valores para a incógnita x (ou para a incógnita y) e, a
seguir, calculando-se o valor da outra incógnita.
Exemplos:
a) Determinar pelo menos três pares ordenados que sejam soluções da equação
2x + y = 3 .
Vamos atribuir valores arbitrários para x, calculando em seguida o valor de y:
2
Para x = 1 Para x = −4 Para x =
3
2x + y = 3 2x + y = 3 2x + y = 3
2 ⋅1 + y = 3 2 ⋅ (−4) + y = 3 2
2⋅ + y = 3
2+ y =3 −8+ y = 3 3
y =3−2 y =3+8 4
+ y =3
y =1 y = 11 3
(−4,11) 4
(1,1) y =3−
3
9−4
y=
3
5
y=
3
 2 5
 , 
 3 3
 2 5
Logo, os pares (1, 1), (−4, 11) e  ,  são algumas das soluções da equação
 3 3
2x + y = 3 .

6. 5
b) Determinar uma solução da equação 3 x − 7 y = −12 , na qual y = 6.
3 x − 7 y = −12
3 x − 7 ⋅ 6 = −12
3 x − 42 = −12
3 x = −12 + 42
3 x = 30
30
x=
3
x = 10
Logo, o par ordenado (10, 6) é uma solução da equação.
c) Sabe-se que 2 x + 3 y = 7 . Se x = 2m + 1 e y = m − 3 , determinar o valor de m,
de x e de y.
2x + 3 y = 7 Vamos calcular o valor de x e de y:
2 ⋅ (2m + 1) + 3 ⋅ (m − 3) = 7 x = 2m + 1 y = m−3
4m + 2 + 3m − 9 = 7 x = 2⋅ 2 +1 y = 2−3
7m − 7 = 7 x = 4 +1 y = −1
7m = 7 + 7 x=5
7 m = 14
Portanto, m = 2, x = 5 e y = −1.
14
m=
7
m=2
d) Sabe-se que y = 10 − 3 x . Nessas condições, determinar o valor de x na
equação 7 x − 3 y = 18 .
7 x − 3 y = 18
7 x − 3 ⋅ (10 − 3 x) = 18
7 x − 30 + 9 x = 18
16 x = 18 + 30
16 x = 48
48
x=
16
x=3
Logo, temos x = 3.

7. 6
Par ordenado e plano cartesiano
Em 1637, ao publicar seu livro La Geométrie, o filósofo e matemático francês
René Descartes lançou a idéia de que um par de números, disposto numa certa
ordem, poderia determinar uma posição no plano.
Usamos o sistema de Descartes, conhecido como sistema de coordenadas
cartesianas, para fazer, por exemplo, gráficos, mapas de ruas ou mapas-mundi.
Vamos ver como se constrói um sistema de coordenadas cartesianas:
• partindo-se de um ponto de referência, são traçadas duas retas
perpendiculares e orientadas;
• cada reta orientada é chamada de eixo. Observe que o sentido de cada eixo
indica o crescente dos números;
• o eixo horizontal é chamado de eixo das abscissas ou normalmente eixo x;
• o eixo vertical é chamado de eixo das ordenadas ou normalmente eixo y;
• o ponto de intersecção dos dois eixos recebe o nome de origem do sistema, e
corresponde ao par ordenado (0,0);
• nos eixos, a cada ponto fazemos corresponder um número: os números
positivos à direita e acima da origem; os números negativos à esquerda e
abaixo da origem.
• o sistema assim formado recebe o nome de plano cartesiano.
• os eixos x e y dividem o plano cartesiano em quatro partes iguais, chamadas
quadrantes:
Dessa maneira um ponto P (x, y) pode ser representado por um par de números
que chamamos de par ordenado. O primeiro número do par indica a abscissa do
ponto e o segundo número indica a ordenada. Por exemplo, P (3, 4), teria sua
representação assim:

8. 7
Gráfico da equação ax + by = c
Considere a equação x + y = 2 . Vamos escolher algumas soluções dessa equação
e desenhar os gráficos dessas soluções.
x y =2− x ( x, y)
0 y =2−0=2 (0, 2)
1 y = 2 −1 = 1 (1, 1)
2 y =2−2=0 (2, 0)
−1 y = 2 − (−1) = 3 (−1, 3)
3 y = 2 − 3 = −1 (3,−1)
Para construirmos o gráfico dessa equação, temos que utilizar esses pares
ordenados, onde o primeiro valor de cada par ordenado é o valor de x e o
segundo valor é sempre o valor de y.
A construção de qualquer gráfico é feita no plano cartesiano, que tem o eixo x e
o eixo y. Esses pares ordenados quando colocados no gráfico representam
pontos do gráfico, veja:

9. 8
Observe que todos os pontos do gráfico estão alinhados, portanto, ligando esses
pontos, temos uma reta.
Essa reta é a representação gráfica da equação x + y = 2 e contém todos os
pontos soluções da equação. Como a reta é uma figura geométrica formada por
infinitos pontos, podemos concluir que existem infinitos valores que satisfazem
a equação x + y = 2 .
OBS.: Embora dois pontos sejam suficientes para traçar uma reta, é conveniente
escolher ao menos um terceiro ponto para comprovação.

10. 9
► Veja como desenhamos a reta a qual pertencem todos os pontos que
representam as soluções da equação 2 x + y = 1 .
x y = 1 − 2x (x, y)
1 y = 1 − 2 ⋅ 1 = −1 (1, −1)
2 y = 1 − 2 ⋅ 2 = −3 (2, −3)
−2 y = 1 − 2 ⋅ (−2) = 5 (−2, 5)
Sistema de duas equações do 1º grau com duas incógnitas
Os sistemas de equação são ferramentas muito comuns na resolução de
problemas em várias áreas (matemática, química, física, engenharia,...) e
aparecem sempre em concursos e exames, como é o caso do vestibular.
Consideremos a seguinte situação:
► A soma de dois números é 12 e a diferença entre eles é 4. Quais são estes
números?
Para a resolução de problemas como este que apresenta duas incógnitas
desconhecidas, utilizamos um sistema de equações.
Chamamos de x o primeiro número (o maior) e de y o segundo número.

11. 10
Pelo enunciado:
» a soma de dois números é 12, ou seja: x + y = 12 (I)
» a diferença entre eles é 4, isto é: x − y = 4 (II)
Como as duas equações se referem ao mesmo fato, elas são ligadas pelo
conectivo “e” e, em Matemática, dizemos que formam um sistema de duas
equações do 1º grau com duas incógnitas, x e y, e indicamos por:
x + y = 12
x− y=4
A solução de um sistema de duas equações do 1º grau com duas variáveis é um
par ordenado (x, y) de números reais que satisfaz as duas equações (I e II).
Verificando o par ordenado (8, 4), notamos que satisfaz as duas equações:
x + y = 12 x− y=4
8 + 4 = 12 8−4= 4
12 = 12 (V ) 4 = 4 (V )
Logo a solução do sistema é (8, 4).
Convém notar que cada uma das equações, quando consideradas isoladamente,
tem infinitas soluções, mas o sistema de equações por elas formado tem uma
única solução, quando ela existe.
Solução de um sistema de duas equações do 1º grau com duas incógnitas
Já sabemos como formar um sistema de equações do 1º grau com duas
incógnitas. Sabemos também que o sistema apresenta uma única solução,
quando ela existe. Como faremos para descobrir que o para ordenado (3, 1) é a
solução do sistema de equações formado pelas equações x + y = 4 e 2 x + y = 7 ?
Vejamos agora os métodos para a resolução de sistema de equações.

12. 11
Método da substituição
Esse método consiste em:
• Isolar uma das incógnitas numa das equações.
• Substituir a expressão do valor desta incógnita na outra equação.
• Resolver a equação do 1º grau assim obtida.
x+ y=4
Vamos agora resolver o sistema
2x + y = 7
1º Passo: Isolamos uma das incógnitas em uma das equações. Escolhemos a
incógnita que for mais fácil de isolar. Se alguma delas tiver coeficiente um, é
essa que devemos escolher. Nesse caso, será o x na primeira equação:
x+ y=4
x =4− y
2º Passo: Na outra equação vamos substituir a incógnita x pelo seu valor 4 − y e
descobrir o valor da incógnita y:
2x + y = 7
2 ⋅ (4 − y) + y = 7
8 − 2y + y = 7 Para facilitar os cálculos, podemos obter uma
equação equivalente com sinais trocados
− y = 7 −8
multiplicando ambos os membros por (–1)
− y = −1 (−1)
y =1
3º Passo: Substituindo o valor de y em x = 4 − y , determinamos o valor da
incógnita x:
x =4− y
x = 4 −1
x=3

13. 12
Verificação:
» 1ª equação: » 2ª equação:
x+ y=4 2x + y = 7
3 +1 = 4 2 ⋅3 +1 = 7
4 = 4 (V) 6 +1 = 7
7 = 7 (V )
Logo, a solução do sistema é dada pelo par ordenado (3, 1).
Método da comparação
Esse método consiste em:
• Isolar uma mesma incógnita em cada equação.
• Igualar as duas expressões.
• Resolver a equação do 1º grau assim obtida.
x+ y=4
Vamos agora resolver o sistema
2x + y = 7
1º Passo: Escolhemos uma das incógnitas, x ou y, isolando-a em ambas as
equações. Optamos, nesse caso, pela incógnita x:
» Na primeira equação: » Na segunda equação:
x+ y=4 2x + y = 7
x = 4 − y (I) 2x = 7 − y
7− y
x= (II)
2

14. 13
2º Passo: Se a incógnita x pode ser expressa na forma ( 4 − y ) e na forma
7− y
  , então essas duas expressões são iguais. Portanto, comparando as
 2 
igualdades (I) = (II), podemos descobrir o valor da incógnita y:
7− y
4− y =
2
2 ⋅ ( 4 − y ) 1 ⋅ (7 − y )
=
/
2 2/
2 ⋅ ( 4 − y ) = 1 ⋅ (7 − y )
8 − 2y = 7 − y
− 2y + y = 7 − 8
− y = −1 (−1)
y =1
3º Passo: Substituindo o valor de y (que nesse caso é 1) em qualquer uma das
expressões onde o x aparece isolado, (I) ou (II), determinamos o valor da
incógnita x:
» Substituindo na equação (I): » Substituindo na equação (II):
x =4− y 7− y
x=
x = 4 −1 2
x=3 7 −1
x=
2
6
x=
2
x=3
Logo, a solução do sistema é dada pelo par ordenado (3, 1).

15. 14
Método da adição
Esse método consiste em:
• Multiplicar cada equação pelo número que nos interessa de modo que uma
incógnita tenha coeficientes opostos nas duas expressões.
• Somar as equações do sistema para obter uma outra equação com uma única
incógnita.
• Resolver a equação do 1º grau assim obtida.
x+ y=4
Vamos agora resolver o sistema
2x + y = 7
1º Passo:
» Em primeiro lugar, vamos escolher a incógnita que queremos eliminar; por
exemplo, x. A incógnita x tem coeficiente 2 na segunda equação e coeficiente 1
na primeira.
−
» Multiplicamos a primeira equação por (−2) para obter outra equivalente, na
qual a incógnita x apareça com o coeficiente (−2): − 2 x − 2 y = −8 .
» Efetuamos, então, a soma das duas equações:
− 2 x − 2 y = −8
2x + y = 7
0 − y = −1 (−1)
y =1

16. 15
2º Passo: Substituindo o valor de y (que nesse caso é 1) em qualquer uma das
equações do sistema, determinamos o valor da incógnita x:
» Substituindo na primeira equação: » Substituindo na segunda equação:
− 2 x − 2 y = −8 2x + y = 7
− 2 x − 2 ⋅ 1 = −8 2x + 1 = 7
− 2 x − 2 = −8 2x = 7 − 1
− 2 x = −8 + 2 2x = 6
− 2 x = −6 6
x=
−6 2
x=
−2 x=3
x=3
Logo, a solução do sistema é dada pelo par ordenado (3, 1).
Exemplos:
x − 2 y = −1
a) Resolva o sistema de equações
− 2x + 4 y = 2
Resolvendo pelo método da substituição temos:
Isolando x na 1ª equação: Substituindo o valor de x Existem infinitos pares
x − 2 y = −1 na 2ª equação: ordenados que satisfazem
− 2x + 4 y = 2 o sistema. Neste caso
x = 2y −1 dizemos que o sistema é
− 2 ⋅ (2 y − 1) + 4 y = 2 indeterminado.
− 4y + 2 + 4y = 2
− 4y + 4y = 2 − 2
0y = 0

17. 16
x − y = −1
b) Resolva o sistema de equações
x − y = −3
Resolvendo pelo método da substituição temos:
Isolando x na 1ª equação: Substituindo o valor de x Não existe y que
x − y = −1 na 2ª equação: satisfaça a equação,
x − y = −3 portanto o sistema não
x = y −1 tem solução. Neste caso
( y − 1) − y = −3 dizemos que o sistema é
y − 1 − y = −3 impossível.
0 y = −3
Representação gráfica de um sistema de duas equações do 1º grau com
duas incógnitas
Para obter graficamente a solução de um sistema de duas equações de 1º grau
com duas incógnitas, vamos representar graficamente cada equação.
Sabemos que a representação gráfica de uma equação linear é uma reta;
portanto, a representação gráfica de duas equações consiste em duas retas que
têm as seguintes possibilidades:
1) As retas cortam-se em um ponto.
2) As retas coincidem.
3) As retas são paralelas.
Essas três possibilidades têm interpretações distintas:
• No primeiro caso, o sistema tem exatamente uma solução. O ponto comum, ou
de interseção das retas obtidas, é a solução do sistema.
• No segundo caso, o sistema tem infinitas soluções, portanto é indeterminado.
• No terceiro caso, o sistema não tem solução, portanto é impossível.
Devemos observar que este método é apenas aproximado.

18. 17
Exemplos:
Caso 1
x+ y=4
Resolva graficamente o sistema
2x + y = 7
Veja como desenhamos a reta a qual pertencem todos os pontos que representam
as soluções das equações x + y = 4 e 2 x + y = 7 .
» Isolando y na 1ª equação: » Isolando y na 2ª equação:
x+ y=4 2x + y = 7
y =4− x y = 7 − 2x
x y =4− x (x, y)
0 y =4−0=4 (0, 4)
1 y = 4 −1 = 3 (1, 3)
−2 y = 4 − (−2) = 6 (−2, 6)
x y = 7 − 2x (x, y)
0 y = 7 − 2⋅0 = 7 (0, 7)
1 y = 7 − 2 ⋅1 = 5 (1, 5)
2 y = 7 − 2⋅2 = 3 (2, 3)
Verificação:
» 1ª equação: » 2ª equação:
x+ y=4 2x + y = 7
3 +1 = 4 2 ⋅3 +1 = 7
4 = 4 (V) 6 +1 = 7
7 = 7 (V )
Logo, a solução do sistema é dada pelo par ordenado (3, 1).

19. 18
Caso 2
x − 2 y = −1
Resolva graficamente o sistema
− 2x + 4 y = 2
Veja como desenhamos a reta a qual pertencem todos os pontos que representam
as soluções das equações x − 2 y = −1 e − 2 x + 4 y = 2 .
» Isolando x na 1ª equação: » Isolando x na 2ª equação:
x − 2 y = −1 − 2x + 4 y = 2
x = 2y −1 − 2 x = −4 y + 2 (−1)
2x = 4 y − 2
4y − 2
x=
2
2 ⋅ (2 y − 1)
x=
2
x = 2y −1
y x = 2y −1 (x, y)
0 x = 2 ⋅ 0 − 1 = −1 (−1, 0)
1 x = 2 ⋅1 − 1 = 1 (1, 1)
2 x = 2 ⋅ 2 −1 = 3 (3, 2)
y x = 2y −1 (x, y)
0 x = 2 ⋅ 0 − 1 = −1 (−1, 0)
1 x = 2 ⋅1 − 1 = 1 (1, 1)
2 x = 2 ⋅ 2 −1 = 3 (3, 2)
O sistema tem infinitas soluções, pois os gráficos das duas equações são
coincidentes. Logo, a solução do sistema é indeterminada.

20. 19
Caso 3
x − y = −1
Resolva graficamente o sistema
x− y =3
Veja como desenhamos a reta a qual pertencem todos os pontos que representam
as soluções das equações x − y = −1 e x − y = −3 .
» Isolando x na 1ª equação: » Isolando x na 2ª equação:
x − y = −1 x − y = −3
x = y −1 x = y −3
y x = y −1 (x, y)
0 x = 0 − 1 = −1 (−1, 0)
2 x = 2 −1 = 1 (1, 2)
4 x = 4 −1 = 3 (3, 4)
y x = y −3 (x, y)
3 x = 3−3= 0 (0, 3)
5 x =5−3= 2 (2, 5)
7 x = 7−3= 4 (4, 7)
O sistema não tem solução, os gráficos das duas equações são retas paralelas.

21. 20
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
BRASIL ESCOLA. Disponível em: <http://www.brasilescola.com>. Acesso em:
17 de agosto de 2008.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
EXATAS. Disponível em: <http://www.exatas.mat.br>. Acesso em: 17 de agosto
de 2008.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
GUELLI, Oscar. Matemática: uma aventura do pensamento. São Paulo:
Ática, 1998.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
KLICK EDUCAÇÃO: O PORTAL DA EDUCAÇÃO. Disponível em:
<http://www.klickeducacao.com.br>. Acesso em: 19 de agosto de 2008.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.