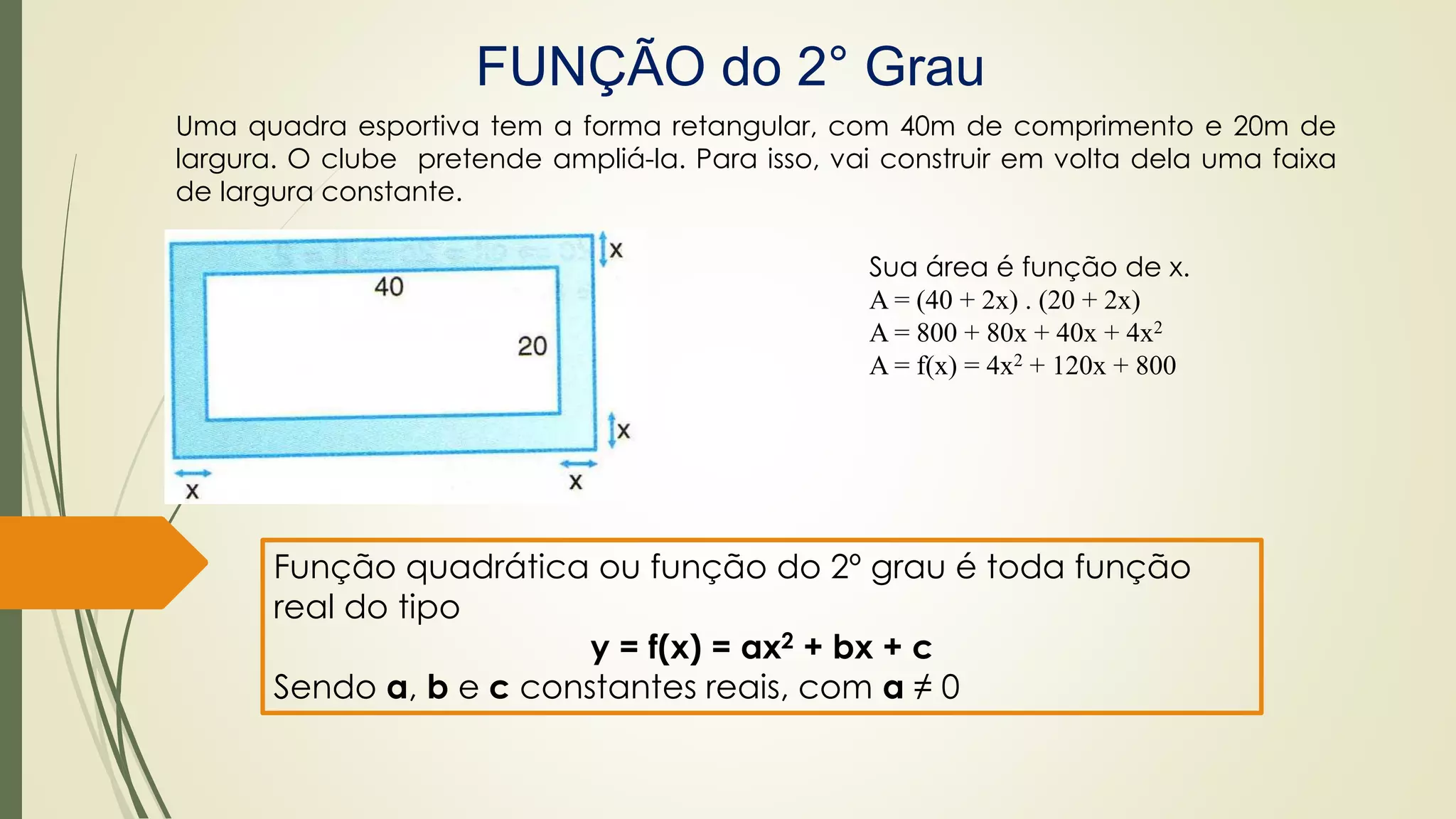
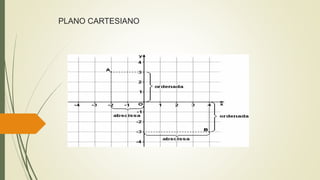
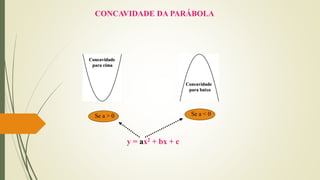
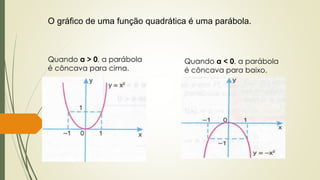
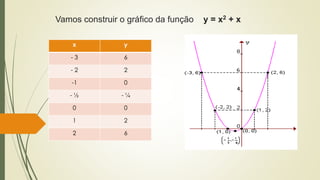
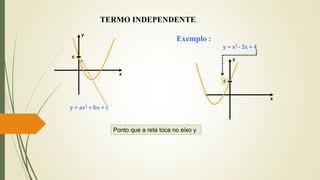
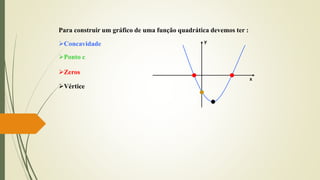
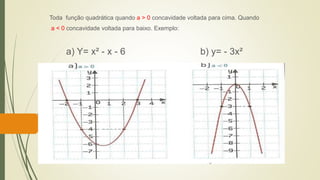
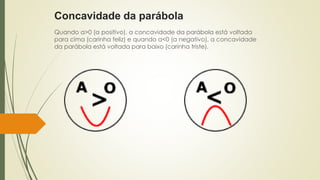
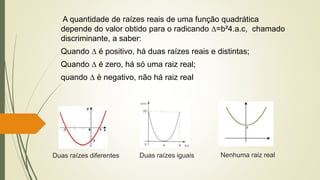
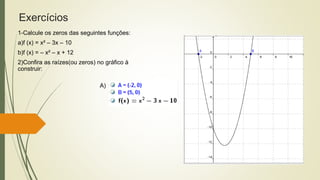
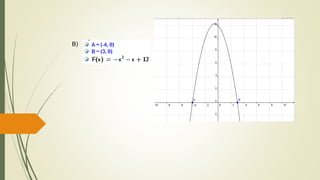
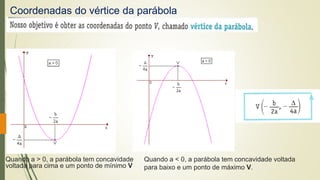
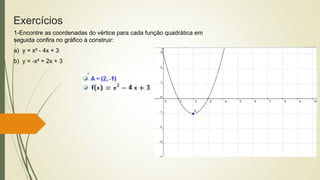
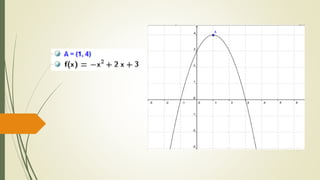
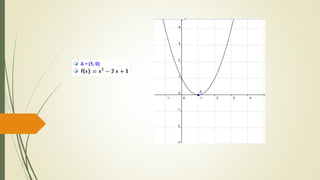
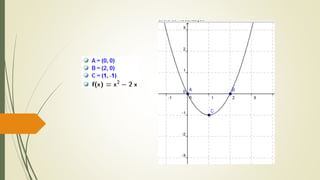
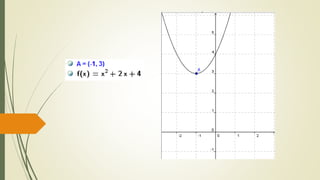
O documento discute funções quadráticas. Explica que uma função quadrática relaciona uma variável independente x com uma variável dependente y através de uma equação do tipo y = ax2 + bx + c, onde a, b e c são constantes. Também mostra como interpretar os gráficos de funções quadráticas e identificar suas propriedades como vértice, raízes e concavidade.

1. FUNÇÃO do 2° Grau
Uma quadra esportiva tem a forma retangular, com 40m de comprimento e 20m de
largura. O clube pretende ampliá-la. Para isso, vai construir em volta dela uma faixa
de largura constante.
Sua área é função de x.
A = (40 + 2x) . (20 + 2x)
A = 800 + 80x + 40x + 4x2
A = f(x) = 4x2 + 120x + 800
Função quadrática ou função do 2º grau é toda função
real do tipo
y = f(x) = ax2 + bx + c
Sendo a, b e c constantes reais, com a ≠ 0

2. Chama-se função quadrática, ou função polinomial do 2º grau,
qualquer função f de IR em IR dada por uma lei da forma
f(x) = ax2 + bx + c, onde a, b e c são números reais e a ≠ 0.
y=ax²+bx+c

3. Vejamos alguns exemplos de função quadráticas:
f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2 -1, onde a = 1, b = 0 e c = -1
f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
f(x) = -4x2, onde a = - 4, b = 0 e c = 0

4. PLANO CARTESIANO

5. O gráfico de uma função polinomial do 2º
grau, y = ax2 + bx + c, com a ≠ 0, é uma
curva chamada parábola

6. CONCAVIDADE DA PARÁBOLA
Se a > 0 Se a < 0
Concavidade
para cima
Concavidade
para baixo
y = ax2 + bx + c

7. O gráfico de uma função quadrática é uma parábola.
Quando a > 0, a parábola
é côncava para cima.
Quando a < 0, a parábola
é côncava para baixo.

8. Trajetória de um salto de ginástica
olímpica

10. Vamos construir o gráfico da função y = x2 + x
x y
- 3 6
- 2 2
-1 0
- ½ - ¼
0 0
1 2
2 6

11. Ao construir o gráfico de uma função quadrática
y = ax2 + bx + c, notaremos sempre que:
•se a > 0, a parábola tem a concavidade voltada
para cima;
•se a < 0, a parábola tem a concavidade voltada
para baixo;

12. Identificação de coeficientes da função quadrática
2x2 - 3x + 5 = 0
a = 2
b =-3
c = 5
-x2 + 4x - 3 = 0
a =-1
b = 4
c = -3
4x + 8x2 - 4 = 0
a = 8
b = 4
c = -4
3x - 6x2 = 0
a = -6
b = 4
c = -4

13. TERMO INDEPENDENTE
c
y
x
y = ax2 + bx + c
Exemplo :
4
y
x
y = x2 - 2x + 4
Ponto que a reta toca no eixo y

14. Para construir um gráfico de uma função quadrática devemos ter :
Concavidade
Ponto c
Zeros
Vértice
y
x

15. Seja a função definida por y = - x²+ 2x - 2
vamos atribuir para x os valores -1, 0, 1, 2 e 3 calcular os valores de y.
x - x² + 2x - 2 y P (x,y)
-1
0
1
2
3
x - x² + 2x - 2 y P (x,y)
-1 - (-1)² +2.(-1) - 2 -5 (-1,-5)
0 - 0² + 2.0 - 2 -2 (0,-2)
1 - 1² + 2.1 - 2 -1 (1,-1)
2 - 2² + 2.2 - 2 -2 (2,-2)
3 - 3² + 2.3 - 2 -5 (3,-5)

16. Toda função quadrática quando a > 0 concavidade voltada para cima. Quando
a < 0 concavidade voltada para baixo. Exemplo:
a) Y= x² - x - 6 b) y= - 3x²

17. Concavidade da parábola
Quando a>0 (a positivo), a concavidade da parábola está voltada
para cima (carinha feliz) e quando a<0 (a negativo), a concavidade
da parábola está voltada para baixo (carinha triste).

18. Zeros ou Raízes
Chama-se zeros ou raízes da função polinomial do
2º grau f(x) = ax2 + bx + c ,a ≠ 0, os números reais x
tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as
soluções da equação do 2º grau ax2 + bx + c = 0, as
quais são dadas pela chamada fórmula de Bháskara:
Denominam-se raízes da função do 2º grau os valores de x para os
quais ela se anula.
Como determinar a raiz ou zero da Função do 2º grau?
Simplesmente aplicando a resolução de equações do 2º grau :

19. A quantidade de raízes reais de uma função quadrática
depende do valor obtido para o radicando ∆=b²4.a.c, chamado
discriminante, a saber:
Quando ∆ é positivo, há duas raízes reais e distintas;
Quando ∆ é zero, há só uma raiz real;
quando ∆ é negativo, não há raiz real
Duas raízes diferentes Duas raízes iguais Nenhuma raiz real

20. Exercícios
1-Calcule os zeros das seguintes funções:
a)f (x) = x² – 3x – 10
b)f (x) = – x² – x + 12
2)Confira as raízes(ou zeros) no gráfico à
construir:
A)

21. B)

22. Coordenadas do vértice da parábola
Quando a > 0, a parábola tem concavidade
voltada para cima e um ponto de mínimo V
Quando a < 0, a parábola tem concavidade voltada
para baixo e um ponto de máximo V.

23. 1-Encontre as coordenadas do vértice para cada função quadrática em
seguida confira no gráfico à construir:
a) y = x² - 4x + 3
b) y = -x² + 2x + 3
Exercícios

25. O valor do coeficiente a define a concavidade da parábola;
Os zeros definem os pontos em que a parábola intercepta o eixo dos
x;
O vértice V indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
A reta que passa por V e é paralela ao eixo dos y é o eixo de simetria
da parábola;
Para x = 0 , temos y = a · 02 + b · 0 + c = c; então (0, c) é o ponto em
que a parábola corta o eixo dos y.

26. a)
a=1 ,concavidade para cima
∆=0 , x’ = x” =1
V=(1,0)
b)
a=1 ,concavidade voltada para cima
∆=4 >0 ,x’=0 e x”=2
V=(2,-1)
c)
a=1 ,concavidade voltada para cima
∆=-12 <0 , não tem raiz real
V=(-1,3)
1. F(x) = x² – 2x +1
2. F(x) = x² - 2x
3. F(x) = x² + 2x + 4
Exercícios