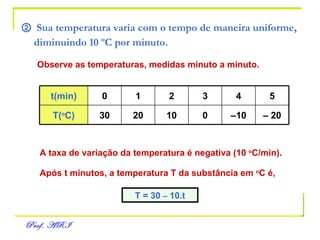
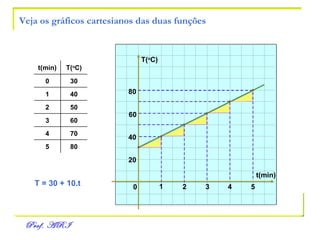
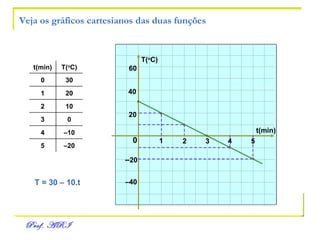
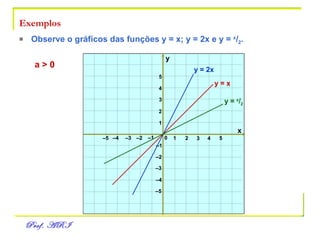
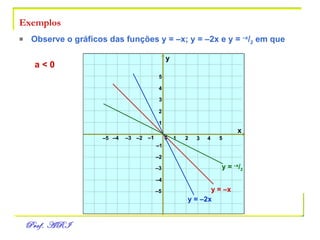
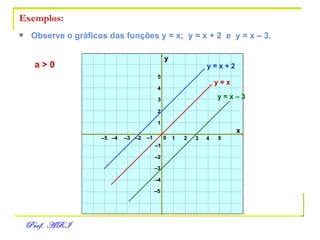
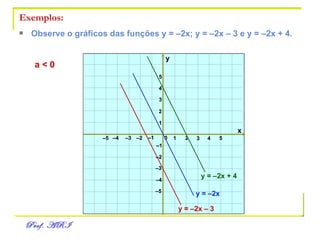
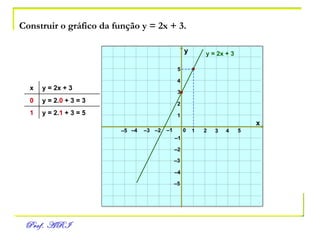
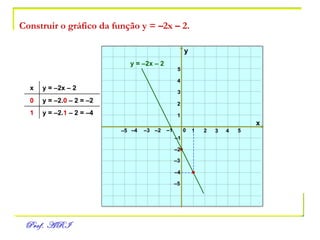
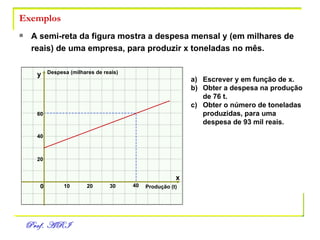
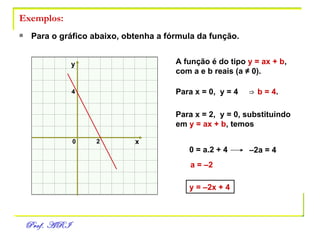
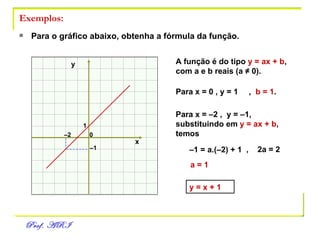
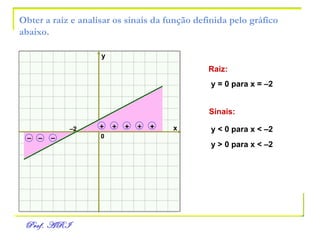
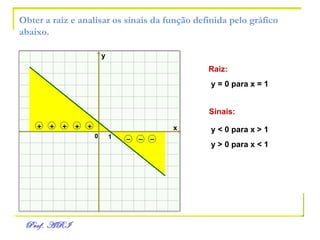
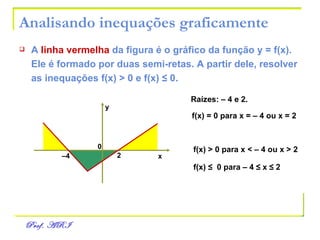
O documento discute funções afins, definidas como funções do tipo y = ax + b. Apresenta exemplos de situações em que a temperatura varia linearmente com o tempo e constrói os respectivos gráficos. Explica como obter a equação de uma função a partir de dois pontos e analisa propriedades como raiz, crescimento e estudo de sinal.

1. FUNÇÃO AFIM

2. A temperatura de uma substância é 30 ºC. Vamos analisar duas situações distintas.

3. ① Sua temperatura varia com o tempo de maneira uniforme, aumentando 10 ºC por minuto. Observe as temperatura, medidas minuto a minuto. A taxa de variação da temperatura é positiva (10 o C/min). Após t minutos, a temperatura T da substância em o C é, T = 30 + 10.t 80 70 60 50 40 30 T( o C) 5 4 3 2 1 0 t(min)

4. ② Sua temperatura varia com o tempo de maneira uniforme, diminuindo 10 ºC por minuto. Observe as temperaturas, medidas minuto a minuto. A taxa de variação da temperatura é negativa (10 o C/min). Após t minutos, a temperatura T da substância em o C é, T = 30 – 10.t – 20 – 10 0 10 20 30 T( o C) 5 4 3 2 1 0 t(min)

5. Veja os gráficos cartesianos das duas funções t(min) T( o C) 0 1 2 3 4 20 40 60 80 5 T = 30 + 10.t 80 5 70 4 60 3 50 2 40 1 30 0 T( o C) t(min)

6. Veja os gráficos cartesianos das duas funções t(min) T( o C) 0 1 2 3 4 – 20 – 40 20 40 5 T = 30 – 10.t 60 – 20 5 – 10 4 0 3 10 2 20 1 30 0 T( o C) t(min)

7. Função afim ou de 1º grau é toda função do tipo y = f(x) = ax + b Em que a e b são números reais, com a ≠ 0 . Se b = 0 , temos a função y = f(x) = ax , chamada, também , função linear .

8. Exemplos: y = f(x) = 5x – 3 é uma função afim com a = 5 e b = –3. y = f(x) = x/5 + √3 é uma função afim, com a = 1/5 e b = √3 y = f(x) = - x + ½ é uma função afim, com a = –1 e b = 1/2

9. Características da função afim y = f(x) = ax + b. A fórmula que a define é um polinômio de 1º grau ; seu termo independente pode ser nulo ou não. Se b = 0 , temos a função f(x) = ax , chamada de função linear . A constante real a , não-nula, é o coeficiente angular . Ela é a mesma, qualquer que seja o intervalo considerado.

10. Características da função afim y = f(x) = ax + b. A constante real b é o coeficiente linear . Seu gráfico cartesiano é uma linha reta , não paralela aos eixos. Ela pode conter a origem (caso b = 0 ) ou não conter origem (caso b ≠ 0 ). O crescimento ou o decrescimento da função estão relacionados com o sinal de a . A reta é ascendente para a > 0 e descendente para a < 0 .

11. Casos Especiais Função linear b = 0 , f(x) = 3x Função Identidade b = 0 e a = 1 , ou seja, f(x) = x Função constante a = 0 , f(x) = 3

12. CRESCIMENTO E DECRESCIMENTO. a > 0 função crescente reta ascendente ( sobe da esquerda p/ direita ) a < 0 função decrescente reta descendente ( desce da esquerda p/ direita )

13. Exemplos Observe o gráficos das funções y = x; y = 2x e y = x / 2 . x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = x y = x / 2 y = 2x a > 0

14. Exemplos Observe o gráficos das funções y = –x; y = –2x e y = –x / 2 em que x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = –x y = –x / 2 y = –2x a < 0

15. A partir do gráfico da função linear y = ax , podemos obter os gráficos de todas as funções afins y = ax + b . Deslocamos o gráfico da função y = ax para cima ou para baixo , de acordo com o valor da constante b .

16. Exemplos: Observe o gráficos das funções y = x; y = x + 2 e y = x – 3. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = x a > 0 y = x – 3 y = x + 2

17. Exemplos: Observe o gráficos das funções y = –2x; y = –2x – 3 e y = –2x + 4. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = –2x + 4 y = –2x a < 0 y = –2x – 3

18. A análise das duas últimas figuras nos sugere um caso geral em relação a todas as funções afins do tipo y = f(x) = ax + b . Que relação existe entre o coeficiente b e o ponto onde cada reta corta o eixo y? b é a ordenada do ponto em que a reta corta o eixo y . Ou seja, a reta intercepta o eixo y no ponto de coordenadas (0, b) .

19. Construir o gráfico da função y = 2x + 3. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = 2x + 3 y = 2. 1 + 3 = 5 1 y = 2. 0 + 3 = 3 0 y = 2x + 3 x

20. Construir o gráfico da função y = –2x – 2. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = –2x – 2 y = –2. 1 – 2 = –4 1 y = –2. 0 – 2 = –2 0 y = –2x – 2 x

21. Dois pontos determinam uma reta. Por isso, se conhecermos dois de seus pontos, podemos obter a função afim que ela representa. Ou seja, podemos obter os coeficientes a e b da função.

22. Exemplos A semi-reta da figura mostra a despesa mensal y (em milhares de reais) de uma empresa, para produzir x toneladas no mês. Escrever y em função de x. Obter a despesa na produção de 76 t. Obter o número de toneladas produzidas, para uma despesa de 93 mil reais. x y 0 20 30 10 20 40 40 60 Despesa (milhares de reais) Produção (t)

23. Exemplos: Para o gráfico abaixo, obtenha a fórmula da função. A função é do tipo y = ax + b , com a e b reais (a ≠ 0). Para x = 0, y = 4 Para x = 2, y = 0, substituindo em y = ax + b , temos 0 = a.2 + 4 – 2a = 4 a = –2 y = –2x + 4 ⇒ b = 4 . x y 0 2 4

24. Exemplos: Para o gráfico abaixo, obtenha a fórmula da função. A função é do tipo y = ax + b , com a e b reais (a ≠ 0). Para x = 0 , y = 1 Para x = –2 , y = –1, substituindo em y = ax + b , temos – 1 = a.(–2) + 1 , 2a = 2 a = 1 y = x + 1 , b = 1 . x y 0 – 2 1 – 1

25. Raízes e sinal da função afim

26. Nos gráficos das funções de 1º grau, a reta sempre corta o eixo x. A abscissa do ponto por onde o gráfico da função intercepta esse eixo é chamada de zero ou raiz da função. Raiz da função é o valor de x tais que f(x) = 0.

27. Exemplos: Encontrar as raízes das funções de IR em IR definidas por f(x) = 3x – 6 e g(x) = –2x – 2. Queremos obter os valores de x que anulam as duas funções. f(x) = 0 , 3x – 6 = 0 , 3x = 6 , x = 2 g(x) = 0 , –2x – 2 = 0 , –2x = 2 , x = –1

28. Obter a raiz e analisar os sinais da função definida pelo gráfico abaixo. x y 0 – 2 Raiz: y = 0 para x = –2 Sinais: y < 0 para x < –2 y > 0 para x < –2 + + + + + – – –

29. Obter a raiz e analisar os sinais da função definida pelo gráfico abaixo. x y 0 Raiz: y = 0 para x = 1 Sinais: y < 0 para x > 1 y > 0 para x < 1 1 – – – + + + + +

30. Estudar o sinal de uma função é determinar para que valores do domínio (valores de x) a função é positiva, negativa ou nula.

31. Exemplos: Estudar o sinal da função definida por f(x) = 3x – 6. Queremos saber para que valores reais de x a função é positiva, negativa ou nula. f(x) = 0 , 3x – 6 = 0 , 3x = 6 , x = 2 Primeiro vamos achar sua raiz. x 2 Portanto, y = 0 para x = 2 y > 0 para x > 2 y < 0 para x < 2 – +

32. Exemplos: Estudar o sinal da função definida por g(x) = –2x + 2. g(x) = 0 , –2x + 2 = 0 , –2x = –2 , x = 1 Primeiro vamos achar sua raiz. x 1 Portanto, y = 0 para x = 1 y > 0 para x < 1 y < 0 para x > 1 – +

33. Inequações de 1º grau

34. Suponhamos que y = f(x) e y = g(x) sejam duas funções reais. Chamamos Inequação de incógnita x toda desigualdade condicional que apresenta uma das formas seguintes: f(x) > g(x) f(x) < g(x) f(x) ≥ g(x) f(x) ≤ g(x)

35. Solução e Conjunto-solução Solução de uma inequação é cada valor real de x que a satisfaz. Conjunto-solução de uma inequação é o conjunto de todas as soluções. Resolver uma inequação é encontrar o seu conjunto solução.

36. Equivalência de inequações Princípios de equivalência

37. Princípios de equivalência Podemos adicionar uma mesma expressão aos dois membros de uma inequação. Isso equivale a transpor um termo de um membro para outro, invertendo o seu sinal. 3x + 5 > 2 ⇒ 3x > 2 – 5 ⇒ 3x > –3 ⇒ x > –1 Troca de sinal – 3x ≤ 6 – 4x ⇒ – 3x + 4x ≤ 6 ⇒ x ≤ 6 Troca de sinal

38. Princípios de equivalência Podemos multiplicar ou dividir os dois membros de uma inequação por um mesmo número real k (k ≠ 0) . No caso, o sentido da desigualdade se mantém , se k for positivo . se inverte , se k for negativo . 3x > –12 x > –12/3 x > – 4 Manteve o sentido

39. Princípios de equivalência Podemos multiplicar ou dividir os dois membros de uma inequação por um mesmo número real k (k ≠ 0) . No caso, o sentido da desigualdade se mantém , se k for positivo . se inverte , se k for negativo . – 5x ≤ – 15, x ≥ –15/–5 , x ≥ 3 Inverteu o sentido

40. Princípios de equivalência Podemos multiplicar ou dividir os dois membros de uma inequação por um mesmo número real k (k ≠ 0) . No caso, o sentido da desigualdade se mantém , se k for positivo . se inverte , se k for negativo . < 3 , x + 1 > 3.(–2) , x + 1 > –6 Inverteu o sentido , x > –7

41. Analisando inequações graficamente A linha vermelha da figura é o gráfico da função y = f(x). Ele é formado por duas semi-retas. A partir dele, resolver as inequações f(x) > 0 e f(x) ≤ 0. Raízes: – 4 e 2. f(x) = 0 para x = – 4 ou x = 2 f(x) ≤ 0 para – 4 ≤ x ≤ 2 f(x) > 0 para x < – 4 ou x > 2 x y 0 2 – 4