O documento apresenta um resumo sobre conceitos básicos de pré-cálculo, incluindo conjuntos numéricos, expressões algébricas, equações do 1o e 2o grau e inequações. O capítulo 1 discute conjuntos numéricos, operações com números inteiros e racionais, e o capítulo 2 introduz conceitos de funções e o plano cartesiano.

1. Apostila- Pré-Cálculo
Disciplina: Cálculo Diferencial e Integral
Curso: Engenharias
Profª: Gislaine Vieira

2. 2
Capítulo 1 – Matemática Elementar
1.1) Conjuntos Numéricos
• Conjunto dos números Naturais (IN)
,...}4,3,2,1,0{=IN
• Conjunto dos números Inteitos (Z)
,...}3,2,1,0,1,2,3{..., −−−=Z
Notação: }0{,...}3,2,1,1,2,3{...,*
−=−−−= ZZ =conjuntos dos números inteiros não
nulos.
,...}3,2,1{
*
=+Z = conjuntos dos números inteiros positivos.
}1,2,3{...,
*
−−−=−Z = conjuntos dos números inteiros negativos.
OBS:Todo número natural é um número inteiro e, portanto, ZIN ⊂
• Conjunto dos números Racionais (Q)






∈∈= *
/ ZbeZa
b
a
Q
Exemplos:
1
6
6
1
0
0
1
4
4 ==
−
=−
Todo número inteiro é racional. Portanto;
Os decimais exatos
Exemplos:
1000
32131
131,32
100
125
25,1,
100
15
15,0 =−==
Os decimais periódicos(dízimas periódicas)
Exemplos: 1)
3
1
....333,0 =

3. 3
Chamamos r = 0,333..., e multiplicamos ambos os membros por 10, temos:
10 r =3,333.... Subtraindo membro a membro,as equações, vem:
10 r = 3,333...
r = 0,333...
9 r =3
Portanto: 9 r = 3
3
1
9
3
==r
2)
99
31
....313131,0 =
Chamamos r = 0,313131..., e multiplicamos ambos os membros por 2
10 , temos:
100 r =31,313131.... Subtraindo membro a membro,as equações, vem:
100 r = 31,313131...
r = 0,313131...
99 r = 31
Portanto: 9 9 r = 31
99
31
=r
• Conjunto dos números Reais (IR)
O conjunto dos números reais (IR) é formado pelos números racionais e pelos
números irracionais. Os números reais podem ser representados por pontos de uma reta.
Assim, por exemplo, podemos determinar o ponto que representa o número
2 do seguinte modo:
O conjunto IR-Q indica o conjunto dos números irracionais, isto é, o conjunto
dos números reais que não são racionais.
Exemplos: 5)25(2 =−+ (racional)
2222 =+ (irracional)

4. 4
1.2)Número Inteiros -Expressões Numéricas
Calcular as seguintes expressões numéricas:
1) =×+ 853
1ºPasso) =×+ 853 3 + 40 Calcula-se a multiplicação
2ºPasso) 3 + 40 = 43 Depois a soma
2) =÷+ 21819
1ºPasso) =÷+ 21819 19 + 9 Calcula-se a divisão
2ºPasso) 19 + 9 = 28 Depois a soma
3) =×++× 23)47(5
1ºPasso) =×++× 23)47(5 6)11(5 +× Calcula-se primeiro os parênteses
2ºPasso) =+× 6)11(5 55 + 6 Depois a multiplicação
3ºPasso) 55 + 6 = 61 e por último a soma
4) =−÷−÷+ )57(43)93(
1ºPasso) )2(43)12()57(43)93( ÷−÷=−÷−÷+ Calcula-se primeiro os
parênteses
2ºPasso) 24)2(43)12( −=÷−÷ Depois a multiplicação
3ºPasso) 4 – 2 = 2 e por último a soma
Regras dos sinais
5) =+×+ )5()2( +10
6) =+×− )3()2( - 6
7) =−×− )3()2( + 6
8) =−×+ )5()2( -10
9) =+÷+ )5()10( +2
10) =−÷+ )4()24( - 6
11) 81333334
=×××=
11) 9)3()3()3( 2
+=−×−=−
12) 8)2(4)2()2()2()2( 3
−=−×+=−×−×−=−
13) 16)16()2222(24
−=−=×××−=−

5. 5
14)
8
1
2
1
2 3
3
==−
15)
9
4
9
4
1
4
9
1
2
3
1
2
3
2
2
=×==






=





−
Fatoração
16) 8864 2
==
17) 255.5555625 224
====
18) 33 233 53
4222232 ===
Exemplos:
Calcule o valor numérico das expressões:
1) 52
)1()2()3()45(20 −×−+−÷−− =
Resolução:
272520)1()2(94520)1()2()3()45(20 52
=++=−×−+÷+=−×−+−÷−−
2) =÷−−−−+−− 255)325()1()2( 32
1
203
Resolução: =÷−−−+−−=÷−−−−+−− 25125)925(1)8(255)325()1()2( 2
1
32
1
203
= 05418516185)16(18 2
1
=−−+=−−+=−−++
3) =





÷+×





32
3
2
5
2
5
4
4
1
Resolução:
20
27
20
1
40
54
20
1
8
27
5
2
80
4
27
8
5
2
5
4
16
1
3
2
5
2
5
4
4
1
32
+=+=×+=÷+×=





÷+×





=
5
7
20
28
=
4) =÷−××−÷ )4,272,02,13,0(25)5,0( 2
Resolução:
07,0
100
7
50
6
20
1
50
3
2
5
1
4
1
240
72
25
9
25
4
1
24
10
100
72
100
36
25
100
25
10
24
100
72
10
12
10
3
25
10
5
)4,272,02,13,0(25)5,0(
2
2
−=
−
=−=





×−×=





−×−÷=
=





×−×−÷=





÷−××−÷





=÷−××−÷

6. 6
Exercícios
Calcule o valor numéricos da expressões:
1) =4
81 2) =3
1000
3) =−+ 2024553 4) =+−5 4 3
9518.16
Tarefa: Lista 1 de exercícios
1.3)Números Fracionários -Expressões Numéricas
Exemplos:
1)
7
9
7
63
7
6
7
3
=
+
=+
2)
12
17
12
98
12
3.32.4
4
3
3
2
=
+
=
+
=+ (m.m.c(3,4)=12)
3)
15
8
5.3
4.2
5
4
.
3
2
==
4)
5
6
10
12
2
3
.
5
4
3
2
5
4
===÷
Racionalização:
5)
2
23
4
23
2.2
2.3
2
3
===
6)
62
32
62
)3(.)2(
62
)3.2).(3.2(
)3.2(2
3.2
3.2
.
3.2
2
32
2
22
+−=
−
−
==
−
−
=
−+
−
=
−
−
+
=
+
Tarefa: Lista 2 de exercícios
1.4) Produtos Notáveis
1ºCaso)Produto da soma de dois termos
222
2)( bababa ++=+
2ºCaso)Produto da diferença de dois termos
222
2)( bababa +−=−

7. 7
3ºCaso)Produto da soma pela diferença de dois termos
22
)).(( bababa −=−+
4ºCaso)Cubo da soma de dois termos
32233
33)( babbaaba +++=+
5ºCaso)Cubo da diferença de dois termos
32233
33)( babbaaba −+−=−
6ºCaso)Fatoração que envolve Cubos
))(( 2233
babababa +−+=+
))(( 2233
babababa ++−=−
Exercícios:
Simplifique as expressões:
1) =+−−− )1).(1()1( 2
xxx 2) =−+ )32).(32( 22
baba
Simplifique as frações:
1) =
+
ca
acac
2
2
12
104
2) =
+
−
+
−
+
1
1
1
1
x
x
x
x
Tarefa: Lista 3 de exercícios
1.5)Equações do 1º Grau
Chamamos de equação do 1º grau na incógnita x a toda equação que pode ser expressa
na forma: bax = , onde a e b são constante,com 0≠a , e chamamos de coeficientes.
O conjunto-solução é S =






a
b
.

8. 8
Exemplos:
Resolução em IR (IR=conjuntos dos números reais)
1) 3x-1 = 8 2)5x+7 = 2x+13
3x = 9 5x-2x = 13 -7
x = 3 3x = 6
S = {3} x = 2 S = {2}
3) 3
3
52
1
1
=
−
−
+
−
+
x
x
x
x
3
7
073
9123293
)3)(1(3293
3
)3)(1(
)1)(52()3)(1(
22
2
−=
=+
+−=+−
−−=+−
=
−−
−−+−+
x
x
xxxx
xxxx
xx
xxxx
S = {
3
7
− }
1.6)Equações do 2º Grau
Chamamos de equação do 2º grau na incógnita x a toda equação que pode ser expressa
na forma: 02
=++ cbxax , onde a , b e c são constante,com 0≠a , e chamamos de
coeficientes.
• Formula resolutiva da Báskara:.
02
=++ cbxax , 0≠a
a
b
x
2
∆±−
= onde acb 42
−=∆ é chamado discriminante da equação.
Se
)(0
)(0
)(20
21
21
complexassoluçõesexistemmasreaissoluçõesadmitenãoequaçãoA
xxduplaraiztemequaçãoaqueseDiz
xexreaisraizesExistem
⇒<∆
=−⇒=∆
⇒≥∆
• Soma e Produto das Raízes
Sendo 1x e 2x as raízes da equação do 2ºgrau, tem-se:
a
c
xxP
a
b
xxS
==
−=+=
21
21
.

9. 9
Exercícios:
Resolver em IR:
1) 0532
=+− xx
2) 0242 2
=+− xx
3) 0872 2
=+− xx
4) 022
=− xx
5) 092
=−x
6) 022)22(2
=++− xx
Tarefa: Lista 4 de exercícios

10. 10
1.7) Inequações em IR
Resolução em IR:
1) 3x > 12
x > 4
S={ 4/ >∈ xIRx } lê-se: {x pertence aos reais tal que x é maior do que 4}
2) 6x – 1 <11
6x < 10
3
5
6
10
<
<
x
x
S={
3
5
/ <∈ xIRx } lê-se: {x pertence aos reais tal que x é maior do que 5/3}
3) 02 ≤− x
0≥x
S={ 0/ ≥∈ xIRx } lê-se: {x pertence aos reais tal que x é maior ou igual a 0}
Tarefa: Lista 5 de exercícios
Exercícios:
Resolver:
1) 037 ≥+x 2) 039 ≤+− x
3) 3
2
1
−≤
−
x
x
4)
4
1
2
1
3
>
−
−
xx
5) 64312 ≥−≥ x 6) 9553 −≥−−> x

11. 11
Capítulo 2 – Funções
2.1) O Plano Cartesiano
O Ponto A é identificado por: x = 2, y = 4. par ordenado(2,4)
O Ponto B é identificado por: x = 4, y = 2. par ordenado(4,2)
O Ponto A tem abscissa 2 e ordenada 4.
O Ponto B tem abscissa 4 e ordenada 2.
2.2) Função y = f(x)
Sempre que duas grandezas, x e y, estão relacionadas entre si, de modo que:
1. x pode assumir qualquer valor em um conjunto A;
2. a cada valor de x corresponde um único valor de y em um conjunto B;
dizemos que a grandeza que assume valores y é uma função da grandeza que assume
valores x, isto é, que y é uma função de x.
Exemplo: Para construir um galinheiro retangular um carpinteiro dispõe de 12m de tela.
Em um dos lados vai aproveitar uma parede já existente. Veja os desenhos abaixo.
Obter uma expressão que relaciona a área do galinheiro com a medida de um dos lados.
Resolução:
A
B
x
y

12. 12
São dados: y(m²): área do galinheiro e x(m): medida de um lado do retângulo.
Assim, se dois lados medem x, o outro mede 12 – 2x. Logo,
y = x .(12 - 2x) ou y = 12x - 2x²
Desse modo descobrimos uma expressão que relaciona y com x.
A partir dessa lei, podemos construir uma tabela de valores,um diagrama de flechas e
um gráfico cartesiano.
Tabela:
x(m) 0 1 2 3 4 5 6
y(m²) 0 10 16 18 16 10 0
Diagrama de flechas:
Gráfico Cartesiano
0
1
2
3
4
5
0
10
16
18
16
10
Lado x(m) Área y(m²)

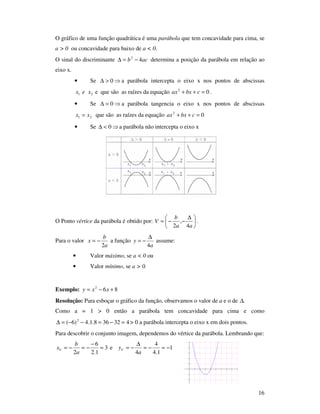
13. 13
O domínio da função é o conjunto dos valores de x para os quais a situação é
possível. No exemplo, o domínio é formado pelos valores reais de x que são positivos e
menores do que 6, isto é, ]0,6[.
O conjunto imagem da função é formado pelos valores correspondentes aos
valores do domínio. No exemplo, o conjunto imagem é formado pelos valores de y que
são positivos e menores ou iguais a18, isto é, ]0,18].
Nova notação para função:
Quando y é uma função de x, escrevemos y = f(x) (lê-se: y é igual a f de x)
Indica-se por: BAf →: uma função em que x assume valores no conjunto A e y
assume os valores no conjunto B.
Exemplo: Considere a função IRf →]2,1[: definida por 2
)( xxf =
Temos que: x assume valores no conjunto [1,2] e y assumi valores no conjunto IR.
2.3) Função Constante
IRIRf →:
f(x) = b onde b é um número real.
O gráfico de uma função constante é uma reta paralela ao eixo x, passando pelo ponto
(0,b).
Exemplo: f(x)= 4
O domínio da função é o conjunto D=IR e a
imagem é o conjunto Im={4}
2.4)Função do 1º Grau ou Função Afim
IRIRf →:
f(x) = ax +b onde a e b são constante e 0≠a .
O gráfico de uma função afim é um conjunto de pontos sobre uma reta.

14. 14
y = 2*x+3
O coeficiente a é chamado de coeficiente angular ou declividade da reta. O coeficiente
angular é a tangente da inclinação da reta, isto é, é a tangente do ângulo que a reta
forma com o eixo x.
αtga =
Sendo ),(),( BBAA yxBeyxA dois pontos distintos da reta, então:
AB
AB
xx
yy
aetga
−
−
== α
O coeficiente b é chamado de coeficiente linear da reta. Para obtê-lo, basta fazer x = 0
em y = ax + b. Daí, y = b. Isso significa que o coeficiente linear é dado pelo ponto
(0,b), intersecção da reta com o eixo y.
Observação: Se b = 0 tem-se f(x) = ax e a função é chamada função linear. Neste caso
a reta passa pela origem do sistema cartesiano.
Exemplo: Construir o gráfico de f(x)= 2x+3
Para determinar a reta é suficiente obter dois pontos distintos dessa reta. Para isso,
simplesmente atribuímos dois valores distintos à variável x e construímos a tabela:
X y = f(x)
0 3
1 5
α

15. 15
Para obter a intersecção da reta com o eixo x, devemos resolver a equação f(x) = 0:
2x+3 = 0 2x = -3
2
3−
=x Portanto a reta intercepta o eixo x no ponto 




 −
0,
2
3
.
O coeficiente linear nos diz que a intersecção da reta com o eixo y é o ponto (0,3).
O conjunto domínio é IR e o conjunto imagem também é IR.
Exercícios:
Esboçar o gráfico e dar o domínio e a imagem.
1) f(x) = -1 2) f(x) = 2x – 6
3) f(x) = -x+3 4) f(x) = 5
Escreva a função do 1º grau representada pela reta:
5) 6)
Tarefa: Lista 9
2.5)Função do 2º Grau ou Função Quadrática
IRIRf →:
cbxaxxf ++= 2
)( onde a,b e c são constantes e 0≠a .

16. 16
O gráfico de uma função quadrática é uma parábola que tem concavidade para cima, se
a > 0 ou concavidade para baixo de a < 0.
O sinal do discriminante acb 42
−=∆ determina a posição da parábola em relação ao
eixo x.
• Se ⇒>∆ 0 a parábola intercepta o eixo x nos pontos de abscissas
21 xex e que são as raízes da equação 02
=++ cbxax .
• Se ⇒=∆ 0 a parábola tangencia o eixo x nos pontos de abscissas
21 xx = que são as raízes da equação 02
=++ cbxax
• Se ⇒<∆ 0 a parábola não intercepta o eixo x
O Ponto vértice da parábola é obtido por: 




 ∆
−−=
aa
b
V
4
,
2
.
Para o valor
a
b
x
2
−= a função
a
y
4
∆
−= assume:
• Valor máximo, se a < 0 ou
• Valor mínimo, se a > 0.
Exemplo: 862
+−= xxy
Resolução: Para esboçar o gráfico da função, observamos o valor de a e o de .∆
Como a = 1 > 0 então a parábola tem concavidade para cima e como
432368.1.4)6( 2
=−=−−=∆ > 0 a parábola intercepta o eixo x em dois pontos.
Para descobrir o conjunto imagem, dependemos do vértice da parábola. Lembrando que:
3
1.2
6
2
=
−
−=−=
a
b
xV e 1
1.4
4
4
−=−=
∆
−=
a
yV

17. 17
y = 3^x
O conjunto domínio é D = IR, e o conjunto imagem é Im = }1/{ −≥∈ yIRy .
Exercícios:
Esboçar o gráfico, dar o domínio e o conjunto imagem de cada função.
1) 122
++= xxy 2) 42
+−= xy
3) 32
+= xy 4) xxy −−= 2
2.6)Função Exponencial
*
: +→ IRIRf
x
axf =)( onde a é um número real positivo e 1≠a .
Sobre a função exponencial x
axf =)( podemos afirmar que:
• Seu gráfico intercepta o eixo y no ponto P(0,1);
• O conjunto-imagem é }0/{ >∈ yIRy ;
• f é uma função crescente se, e somente se, a >1;
• f é uma função decrescente se, e somente se, 0< a <1;
OBS: Uma função é crescente se : 21
21
xx
aaxx <⇔<
Uma função é decrescente se : 21
21
xx
aaxx >⇔<
Exemplo: x
xf 3)( =
A função é crescente, pois a =3 >0. O conjunto domínio é IRD = e o conjunto
imagem é Im = +=>∈ *
}0/{ IRyIRy
x f(x)
0 1
1 3
-1
3
1

18. 18
Exemplo:
x
xf 





=
2
1
)(
A função é decrescente, pois 1
2
1
0 <=< a . O conjunto domínio é IRD = e o conjunto
imagem é Im = +=>∈ *
}0/{ IRyIRy
Exercícios:
Construa uma tabela para os seguintes valores de x: -2, -1, 0, -1 e 2, a seguir, desenhe o
gráfico da função exponencial e dê o seu domínio e seu conjunto imagem.
1)
x
xf 





=
3
1
)( 2) x
xf 2)( =
Tarefa: Lista 8 de exercícios
x f(x)
0 1
1
2
1
-1 2

19. 19
2.7) Logaritmo
Definição: Dados os números reais positivos a e b com 1≠b , chamamos de logaritmo
de a na base b, que indicamos por ablog , ao número x tal que abx
= .
Em símbolo: abxa x
b =⇔=log
Nomenclatura:
I.) Sendo ax blog= temos:
x: logaritmo
a : logaritmando ou antilogaritmo
b: base do logaritmo
II) a10log é chamado de logaritmo decimal de a e convencionou-se, neste caso, escrever
simplesmente alog
III) aelog é chamado de logaritmo neperiano (logaritmo natural) de a e convencionou-
se, neste caso, escrever aln .
O número e é um irracional cujas primeiras casa decimais são 2,71828...
IV) Chama-se co-logaritmo de a na base b ao oposto do logaritmo de a na base b,isto é:
aaco bb loglog −=
Conseqüências da definição
I) 01log =b
II) 1log =bb
III) KbK
b =log
IV) ab ab
=log
Exemplos:
1) 38log2 = pois 823
=
2)
2
1
5log5 = pois 552
1
=
3) 35 3log5
=

20. 20
Exercícios:
Calcule os seguintes logaritmos:
1) =32log2 2) =8log
2
1
3) =01,0log 4) =25log5co
5) Para que valores de x existe )5(log xx − ?
6) Calcule o logaritmo de 4 na base 0,25.
Propriedades dos Logaritmos
Satisfeitas as condições de existência dos logaritmos, tem-se:
1) NMNM bbb loglog).(log +=
2) NM
N
M
bbb logloglog −=





3) MkM b
K
b log.)(log =
4)
b
a
a
c
c
b
log
log
log = (Mudança de base)
Exercícios:
1)Dado que 30,02log ≈ e 47,03log ≈ , obtenha:
a) =6log b) =8log
c) =5log d) =3log2
e) =45log

21. 21
2.8)Circunferência
É o conjunto de todos os pontos do plano eqüidistantes de um ponto fixo desse plano,
chamado centro Todos os pontos dessa circunferência distam r (raio)do ponto O.
Equação Reduzida da circunferência de centro (a,b) e raio r: 22222
)()( rbyax =−+−
Equação Geral: 022 22222
=−++−−+ rbabyaxyx
Exercícios:
Encontre uma equação para as circunferências abaixo:
1) 2)
Diga se as equações abaixo, representam circunferências. Em caso positivo, determine o
raio e o centro.
3) 2522
=+ yx 4) 25)4()3( 22
=−+− yx
5) 368622
−=−−+ yxyx 6) 1
5
1 2
2
=+





+ yx
.O

22. 22
Tarefa: Lista 10 de exercicios
2.9)Elipse
Elipse é o conjunto dos pontos de um plano cuja soma das distâncias a dois pontos fixos
é constantes. Os pontos fixos são chamados de focos.
Equação Reduzida da elipse de centro (h,k) : 1
)()(
2
2
2
2
=
−
+
−
b
ky
a
hx
Equação Geral: 022
=++++ FEyDxCyAx
Exercícios:
Encontre uma equação para as elipses abaixo:
1) 2)
3)
O
a
b

23. 23
Diga se as equações abaixo, representam elipses. Em caso positivo, determine o centro.
3) 100425 22
=+ yx 4) 05284 22
=++−+ yxyx
5) 011191281501625 22
=−−++ yxyx
2.10) Hipérboles
Uma hipérbole é o conjunto de pontos no plano, cujo valor absoluto da diferença das
distancias a dois pontos fixos é uma constante. Os dois pontos fixos são denominados
de focos.
Equação Reduzida da hipérbole centro (h,k) : 1
)()(
2
2
2
2
=
−
−
−
b
ky
a
hx
Equação Geral: 022
=+++++ FEyDxCyBxyAx
Exemplo: 1
22 2
2
2
2
=−
yx
Exercícios:
Esboce as hipérboles:
1) 1
169
22
=−
yx
2) 1
169
22
=−
xy

24. 24
Capítulo 3 – Trigonometria
3.1) Trigonometria no Triângulo Retângulo
Considere o triângulo retângulo abaixo. Definimos:
Seno de um ângulo α agudo como:
H
CO
Hipotenusa
toCatetoOpos
==)sen(α
Co-seno de um ângulo α agudo, como:
H
CA
Hipotenusa
centeCatetoAdja
==)cos(α
Tangente de um ânguloα agudo,
CA
CO
centeCatetoAdja
toCatetoOpos
tg ==)(α
Cotangente de um ângulo α agudo,como:
CO
CA
toCatetoOpos
centeCatetoAdja
g ==)(cot α
Secante de um ângulo α agudo, como:
CA
H
centeCatetoAdja
Hipotenusa
==)sec(α
Co-secante de um ângulo agudo, como :
CO
H
toCatetoOpos
Hipotenusa
==)sec(cos α
Exemplos:
Sabemos que sen(36º) = 0.58, cos(36º) = 0.80 e tg(36º) = 0.72 , Calcular o valor de x
em cada figura:
Resolução:

25. 25
a) cmx
xx
8,5
10
58,0
10
)36sen( =⇒=⇒=°
b) mx
xx
4
5
80,0
5
)36cos( =⇒=⇒=°
c) Kmx
xx
tg 4,14
20
72,0
20
)36( =⇒=⇒=°
Teorema de Pitágoras:
Em todo triangulo retângulo, a soma dos quadrados das medidas dos catetos é igual ao
quadrado da medida da hipotenusa. Isto é:
222
acb =+
Exemplo: Sabendo que α é um ângulo agudo e que
13
5
)cos( =α , calcular )(αtg e
)(cot αg .
Resolução:
Existe um triangulo retângulo com ângulo agudo α tal que o cateto adjacente a α
mede 5 e a hipotenusa mede 13.Chamamos x o valor do cateto oposto ao ângulo agudo.
Pelo teorema de Pitágoras temos :
222
135 =+x
12
144
25169
2
2
=
=
−=
x
x
x
Logo,
5
12
)( ==
centeCatetoAdja
toCatetoOpos
tg α e
12
5
)(cot ==
CO
CA
g α
Exercício: Sabendo que α é um ângulo agudo e que
5
3
)sen( =α , calcular )(αtg e
)(cot αg .

26. 26
Tabela dos Ângulos Notáveis
30º 45º 60º
Sen
2
1
2
2
2
3
Cós
2
3
2
2
2
1
Tg
3
3 1 3
Por convenção:
)sen(sen
))(cos()(cos
))(sen()(sen
αα
αα
αα
kk
nn
nn
=
=
=
Exemplos:
Calcular o valor das expressões:
1)
)º45()º30(sen
)º30(cos)º60cos(
53
2
tg
E
+
+
=
Resolução:
9
10
8
9
4
5
1
8
1
4
3
2
1
1
2
1
2
3
2
1
)º45()º30(sen
)º30(cos
2
1
5
3
2
53
2
==
+
+
=
+













+
=
+
+
=
tg
E
2)
x
xx
E
2cos
4cos2sen
2
+
= para x=15º
Resolução:
3
4
4
3
1
2
3
2
1
2
1
)º30(cos
)º60cos()º30sen(
)º15.2(cos
)º15.4cos()º15.2sen(
222
==








+
=
+
=
+
=E

27. 27
3)Determinar o valor de x na figura:
Resolução:
Como o triangulo BCD é isósceles , pois possui dois ângulos de mesma medida; logo,
CD=BD=20m.
Assim, do triangulo ABD, temos que:
310
202
3
20
º60sen
=
=
==
x
x
x
BD
x
Logo, 310=x m
4) Sabendo que 3,2 == βα tgtg , calcular o valor de x na figura
Resolução:
Vamos introduzir uma variável auxiliar, fazendo DA=y.
Assim do triangulo ABC temos:
y
x
y
x
tg
+
=⇒
+
=
5
2
5
α

28. 28
Do triangulo ABD temos:
y
x
y
x
tg =⇒= 3β
Devemos então resolver o sistema:







=⇒=
+
=
)(
3
3
)(
5
2
II
x
y
y
x
I
y
x
Substituindo (II) em (I), temos:
30
3
5
2 =⇒
+
= x
x
x
Logo, 30=x cm
Exercícios
Determine a medida x nos triângulos retângulos abaixo:
1) 2)
3 Um avião levanta vôo sob ângulo de 30º em relação à linha do horizonte.Quando tiver
percorrido 900m, sua distância em relação ao solo será:
a)410m
b)420m
c)430m
d)440m
e)450m
6
x
30º 7
x
45º

29. 29
4)Em uma rua plana, uma torre AT é vista por dois observadores X e Y sob ângulos de
30º e 60º com a horizontal, como mostra a figura abaixo.
Se a distancia entre os observadores é de 40m, qual é aproximadamente a altura da
torre?(Se necessário, utilize 4,12 = e 7,13 = ).
5)Obter o valor x na figura.
30º
60º
A B
C
100
x

30. 30
3.2) Medidas de arcos e arcos trigonométricos
Medida de Arco
Para medir um arco menor que uma semicircunferência, usaremos o ângulo
central correspondente. A medida de arco é a medida do ângulo central. Na figura,
temos AÔB=m(AB).
• A medida de uma semicircunferência é 180º.
• A medida de uma circunferência ou de um arco de uma volta é 360º.
• A medida de um arco maior é igual a 360º menos a medida do arco menor
correspondente.
Radiano
Um radiano é o arco cujo comprimento é igual ao raio da circunferência que o
contém. Símbolo: rad.
Desse modo, um ângulo central mede 1 rad se, e somente se, determina na
circunferência um arco correspondente de 1 rad.
Para determinarmos a medida de um arco AB em radianos, podemos dividir o
comprimento de AB pelo comprimento do raio r. Assim, sendo l o comprimento do arco
AB:

31. 31
rad
r
l
ABmed =)(
Pela geometria, sabemos que o comprimento da circunferência é rC π2= .
Sendo assim, a medida, em radianos, do arco de volta inteira é:
rad
r
r
Cmed π
π
2
2
)( ==
Como 14,3≈π , temos:
radCmed 28,6)( ≈
No comprimento da circunferência “cabem”, aproximadamente, 6,28 vezes o
comprimento do raio.
Conversão de unidades
Lembrando que o arco de volta inteira mede 360º, ou radπ2 , podemos estabelecer a
seguinte regra-de-três:
yx
rad
___________
2_________º360 π
Ou ainda:
yx
rad
___________
_________º180 π
Disso segue que: 1° é equivalente(~) π
180
1
rad e 1 rad é equivalente a
π
°180
Exemplos: a)Ache a medida equivalente em radianos de 162°
b)Ache a medida equivalente em graus de
12
5π
rad
Resolução:
a) 162° ~162.
180
π
rad

32. 32
162° ~
10
9π
rad
b)
π
ππ °180
.
12
5
~
12
5
rad
°75~
12
5
rad
π
Tarefa: Lista 6
Arcos Trigonométricos
Consideremos, no plano cartesiano XOY,uma circunferência de centro O(0,0) e raio
igual a 1. Sobre essa circunferência são marcados os arcos trigonométricos que:
• Tem origem no ponto A(1,0).
• Tem medidas algébricas positivas, se percorridos no sentido anti-horário.
• Tem medidas algébricas negativas,se percorridos no sentido horário.
Essa circunferência é chamada circunferência trigonométrica ou ciclo
trigonométrico.
Convenções
I) O sistema de coordenadas XOY divide a circunferência trigonométrica em quatro
partes iguais, denominadas quadrantes.
Assim:
• 1° Quadrante: 0° a 90° ou ( 0 rad a
2
π
rad)
• 2° Quadrante: 90° a 180° ou (
2
π
rad a π )

33. 33
• 3° Quadrante: 180° a 270° ou ( π rad a
2
3π
rad)
• 4° Quadrante: 270° a 360° ou (
2
3π
rad a π2 )
Exemplo: 30º está no 1º quadrante , pois 0º < 30 º < 90º
II) Será omitido o símbolo rad nos arcos trigonométricos em radianos.
Simetrias
Se 0º < x < 90º, temos:
Se
2
0
π
<< x ,temos:
Esses arcos trigonométricos são chamados arcos trigonométricos
correspondentes.

34. 34
3.3)Seno e Cosseno de um arco trigonométrico
Considere no plano cartesiano XOY uma circunferência de centro O(0,0) e raio
igual a 1, e seja x a medida de um arco trigonométrico com extremidade em M
Então:
I) Seno do arco de medida x é a ordenada do ponto M
sen x = OD
II) Cosseno do arco de medida x é a abscissa do ponto M
cos x = OC
E, ainda:
• O eixo OY é o eixo dos senos.
• O eixo OX é o eixo dos co-senos.
Exemplo: Sabendo que e 87,0
2
3
º30cos5,0
2
1
º30sen ≅=== , achar um valor
aproximado de:
a) sen 150º e cos 150º
b)sen 210º e cos 210º

35. 35
Solução:
a) θ== º150AP
Então:



−≅−=
==
87,0º30cosº150cos
5,0º30senº150sen
b) θ== º210AP

36. 36
Então:



−≅−=
−=−=
87,0º30cosº210cos
5,0º30senº210sen
O exemplo anterior mostra que há uma relação entre o quadrante e o valor de seno e
cosseno. Sendo θ a medida de um arco e P a sua extremidade, notamos que:
• P no primeiro quadrante: ;0cos0sen >> θθ e
• P no 2º quadrante: 0cos0sen <> θθ e ;
• P no 3º quadrante: 0cos0sen << θθ e
• P no 4º quadrante: 0cos0sen >< θθ e
Sendoθ a medida de um arco com extremidade no 1º quadrante:
• θθθθ cos)º180cos(sen)º180(sen −=−=− e
• θθθθ cos)º180cos(sen)º180sen( −=+−=+ e
• θθθθ cos)º360cos(sen)º360sen( =−−=− e
3.4)Tangente de um arco trigonométrico- Outras relações
trigonométricas
Considere no plano cartesiano XOY uma circunferência de centro O(0,0) e raio
igual a 1, e seja x a medida de um arco trigonométrico com extremidade em M,não
coincidente com B nem com B’.

37. 37
Então:
Tangente de um arco de medida x é a ordenada do ponto T.
tg x = AT
Nota: O eixo paralelo ao eixo das ordenadas, orientado como este e que passa pelo
ponto A, é chamado eixo das tangentes.
Relação entre tangente, seno e co-seno
Seja x a medida de um arco trigonométrico com extremidade no ponto M.
Da figura, os triângulos OAT e COM são semelhantes. Logo:
x
xsenxtg
OC
CM
OA
AT
cos1
=∴=
Assim:
0cos,
cos
≠= x
x
xsen
xtg .

38. 38
Outras relações trigonométrica
Além de seno, co-seno e tangente de um arco, existem mais três relações que, satisfeitas
as condições de existência, são inversas das três primeiras.
I) Co-tangente
0,
cos
cot ≠= xsen
xsen
x
xg
II) Secante
0cos,
cos
1
sec ≠= x
x
x
III) Co-secante
0,
1
cos ≠= xsen
xsen
xec
Conseqüências
a)
xtg
xg
1
cot =
b) xtgx 22
1sec +=
c) xgxec 22
cot1cos +=
d) 1)sec).(cos(sen =αα
e) 1)).(sec(cos =αα
f) 1)).(cot( =αα gtg
Tarefa: Lista 7
3.5)Funções Trigonométricas
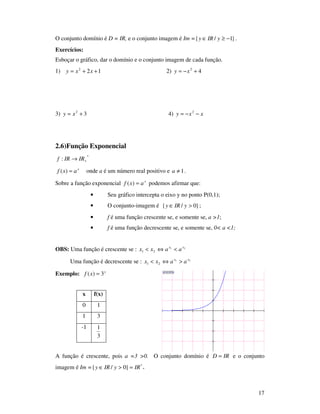
A) Função Seno
Chama-se função seno à função que associa a todo número real, x, a ordenada
do ponto M, imagem de x na circunferência trigonométrica.
Então, podemos definir a função seno como sendo:
xsenxf
IRf
=
−→
)(
]1,1[:

39. 39
Assim:
I) Domínio D = IR
II) Conjunto-imagem IM = [-1,1]
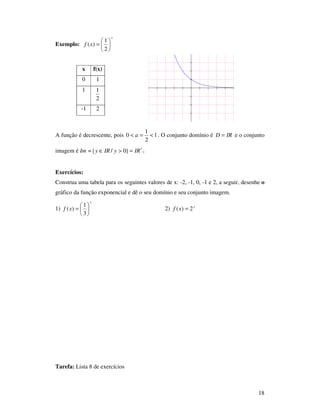
III) Gráfico
Colocando ao pares (x, sen x ) em um sistema de coordenadas cartesianas e unindo
esses pontos, temos uma parte do gráfico da função seno, ou, ainda, uma parte de uma
curva chamada senóide.
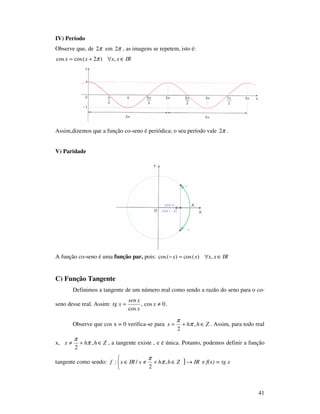
IV) Período
Observe que, de π2 em π2 , as imagens se repetem, isto é:
IRxxxsenxsen ∈∀+= ,)2( π
Assim,dizemos que a função seno é periódica; o seu período vale π2 .O período
é o menor intervalo no qual a função passa por um ciclo completo de sua variação.

40. 40
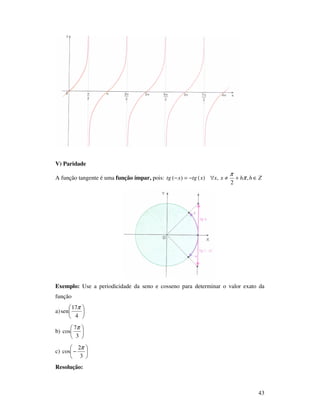
V) Paridade
A função seno é uma função ímpar, pois: IRxxxsenxsen ∈∀−=− ,)()(
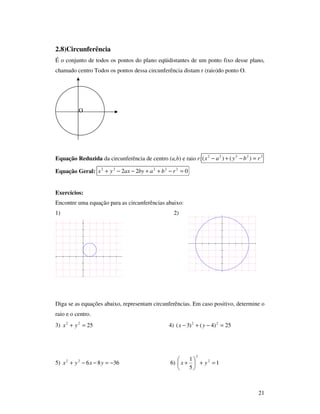
B) Função Co-seno
Chama-se função co-seno à função que associa a todo número real, x, a abcissa
do ponto M, imagem de x na circunferência trigonométrica.
Então, podemos definir a função seno como sendo:
xxf
IRf
cos)(
]1,1[:
=
−→
Assim:
I) Domínio D = IR
II) Conjunto-imagem IM = [-1,1]
III) Gráfico

41. 41
IV) Período
Observe que, de π2 em π2 , as imagens se repetem, isto é:
IRxxxx ∈∀+= ,)2(coscos π
Assim,dizemos que a função co-seno é periódica; o seu período vale π2 .
V) Paridade
A função co-seno é uma função par, pois: IRxxxx ∈∀=− ,)(cos)(cos
C) Função Tangente
Definimos a tangente de um número real como sendo a razão do seno para o co-
seno desse real. Assim: 0cos,
cos
≠= x
x
xsen
xtg .
Observe que cos x = 0 verifica-se para Zhhx ∈+= ,
2
π
π
. Assim, para todo real
x, Zhhx ∈+≠ ,
2
π
π
, a tangente existe , e é única. Potanto, podemos definir a função
tangente como sendo: }



→∈+≠∈ IRZhhxIRxf ,
2
/: π
π
e f(x) = tg x

42. 42
A função tangente associa a todo número real x , Zhhx ∈+≠ ,
2
π
π
, a ordenada
do ponto T, no eixo das tangentes.
Assim:
I)Domínio }



∈+≠∈= ZhhxIRxD ,
2
/ π
π
II) Conjunto-imagem IM = IR
III)Gráfico
IV)Período
Observe que, de π em π , as imagens se repetem, isto é:
Zhxxxtgxtg ∈+≠∀+= ,
2
,)( π
π
π
Assim,dizemos que a função tangente é periódica; e o seu período vale π .

43. 43
V) Paridade
A função tangente é uma função ímpar, pois: Zhhxxxtgxtg ∈+≠∀−=− ,
2
,)()( π
π
Exemplo: Use a periodicidade da seno e cosseno para determinar o valor exato da
função
a) 





4
17
sen
π
b) 





3
7
cos
π
c) 





−
3
2
cos
π
Resolução:

44. 44
a)






4
17
sen
π
=
2
2
4
sen2.2
4
sen4
4
sen
4
16
4
sen
4
16
sen =





=





+=





+=





+=




 + π
π
π
π
πππππ
b) 





3
7
cos
π
=
2
1
3
cos2
3
cos
3
6
cos =





=





+=




 + π
π
πππ
c) 





−
3
2
cos
π
=
2
1
3
4
cos2
3
4
cos
3
64
cos −=





=





−=




 − π
π
πππ