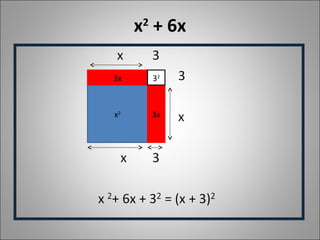
O documento discute equações do segundo grau, incluindo como identificar seus coeficientes, o significado de raízes, como calculá-las usando a fórmula de Bhaskara e o processo de completamento de quadrados. O objetivo é reconhecer e solucionar problemas envolvendo equações do segundo grau.

1. João Marcos Ferreira
Equação do SEgundo
grau
Coeficientes
Equação Completa e incompleta
Raízes: o que significa; como se calcula;
condições para a sua existência.
Soluções particulares de uma equação do 2º Grau
Relação entre os coeficientes e as raízes
Processo do completamento de quadrados

2. Objetivos
• Reconhecer uma equação do 2º Grau
• Identificar os seus coeficientes a, b, c
• Reconher uma equação completa e uma
incompleta, e as condições de existência das
raízes
• Obter as raízes da equação do 2º usando, os
diferentes processo aqui abordados
• Solucionar problemas que envolvam, equação
do 2º Grau
João Marcos Ferreira

3. • Uma equação do tipo ax²+bx+c=0 é
• denominada equação completa do 2º GRAU
• Onde :
• a, b,ca, b,c são coeficientes esão coeficientes e xx a variável ou raiza variável ou raiz
• e a ≠ 0
• O que determina o grau é o expoente da
• Variável x
João Marcos Ferreira

4. João Marcos Ferreira
• Completa
• x² - 4x – 3 = 0, onde a = 1, b = - 4 e c = - 3
• Incompletas
• x² - 9 = 0, onde a = 1, b = 0 e c = - 9
• 6x² = 0, onde a = 6, b = 0 e c = 0
• - 4x² + 2x, onde a = - 4, b = 2 e c = 0
São exemplos de equação do 2º grau:São exemplos de equação do 2º grau:

5. RAÍZES DE UMA EQUAÇÃO DO 2º
GRAU
• Seja a Equação:
• x² - 9 = 0, onde a = 1, b = 0 e c = - 9
• x² = 9 assim, x = ± √9
• X´=3 ou x´´= -3 substituindo-se na equação,
têm-se que:
• (3) ² – 9 = 0 ou (-3) ² – 9 = 0
• As raízes, são valores de x que satisfazem a
igualdade ou seja: são os zeros da equação
João Marcos Ferreira

6. João Marcos Ferreira
A Fórmula de Báscara
Essa fórmula, que permite obter as raízes da equação do
2° grau é conhecida como fórmula de Báscara(1114-
1185, nascido na Índia, o mais importante matemático
do séc. XII
O Nº DE RAIZES ESTÁ ASSOCIADO AO GRAU
DA EQ.

7. João Marcos Ferreira
Existência de Raízes Reais
Denominamos discriminante da equação do 2° grau ax²+bx+c = 0
a expressão b² -4ac, que representamos pela letra grega ∆
Observando a dedução da fórmula de Báscara, podemos concluir
A equação do 2° grau tem raízes reais se, e somente
se, ∆≥ 0.
As raízes são dadas por:
Temos ainda:
∆>0  as duas raízes são números reais distintos.
∆=0  as duas raízes são números reais iguais.
∆<0  não existem raízes reais.

8. João Marcos Ferreira
Exemplo 1

9. João Marcos Ferreira
Exemplo 2
Na equação 9x² + 12x + 4 = 0
Temos: a= 9 b= 12 c= 4
∆=b² -4ac=
∆= 12² - 4.9.4 =
∆=144 – 144=
∆= 0
Como ∆= 0, a equação possui duas raízes reais iguais.
As raízes são:
x’ = -12+ 0 = -2
x= -12 ± √0 = 18 3
2.9 x’’ = -12 – 0 = -2
18 3

10. João Marcos Ferreira
Exemplo 3
Na equação 2x² + 5x + 9 =0
Temos: a= 2 b=5 c= 9
∆=b² -4ac=
∆=5² - 4 .2. 9=
∆= 25 – 72 =
∆= - 47
Como ∆< 0, a equação não possui raízes reais. O conjunto solução
em R é S =Ø.

11. João Marcos Ferreira
Exemplo 04
1- Na equação 054² =−− xx
)5.(1.4)²4(
4²
−−−=∆
−=∆ acb
362016 =+=∆
Como ∆ > 0 a função tem dois zeros reais. Assim:
a
b
x
2
∆±−
=

12. João Marcos Ferreira
Calculemos agora seus zeros:
1.2
36)4( ±−−
=x






−=
−
=
−
=
==
+
=
⇒
±
=
1
2
2
2
64
''
5
2
10
2
64
'
2
64
x
x
x
Logo, os zeros da função são – 1 e 5

13. SOLUÇÕES PARTICULARES
• ax²+bx=0 portanto, c=0
• têm-se fatorando que: x(ax+b)=0
• Ou seja: x=0 ou ax+b=0, donde se conclui
• Que ax=-b e x= -b/a
• Logo as raizes são: x´=0 ou x´´=-b/a
• Seja: 3x² -5x=0 fatorando x: x(3x-5)=0
• Assim: x´=0 ou 3x-5=0 logo 3x=5 e x´´=5/3
João Marcos Ferreira

14. Relações entre coeficientes e
raízes
Se em ax²+bx+c=0, a=1
Temos então que x²+bx+c=0.
Pode-se demonstrar que as raízes da equação,
nesse caso, serão tais que:
x´+x´´= -b e x´.x´´=c ,
logo em x²-5x+6=0 temos
Mentalmente que: x´=2 e x´´=3
João Marcos Ferreira

15. Processo do completamento de
quadrados
• Baseado na interpretação geométrica
dada pelos gregos a (a + b)2
• Al-Khowarizmi, século IX, estabeleceu
um processo geométrico para resolução
de Equação do 2o
Grau Completa.

16. Representação Geométrica
a2
ab
ab
b2

17. x2
+ 6x
x2
3x
3x
32

18. Resolução da equação
x2
+ 6x + 8 = 0
• Passa 8 para o 2o
membro
x2
+ 6x = - 8
• Como na representação geométrica
acrescentamos 32
x2
+ 6x + 32
= - 8 + 32
(x + 3)2
= - 8 + 9
(x + 3)2
= 1

19. • Tira-se então, a raiz quadrada de ambos
os membros
(x + 3) = ± 1
x + 3 = 1 x = 1 – 3 x´ = - 2
x + 3 = - 1 x = - 1 – 3 x´´ = - 4
S = {- 4, -2}

20. Seja Equação: x2
– 2x – 8 = 0
• Teremos então x2
– 2x = 8, passando 8
• como na representação geométrica
acrescentamos 12
aos dois membros teremos
• x2
– 2x + 12
= 12+
8 logo (x – 1)2
= 9
• Extraimos a raiz quadrada : (x – 1) = ± 3
• Calculemos 1º raiz x – 1 = 3, x´ = 4
• Calculemos a 2ª raiz : x – 1 = - 3 e X´´ = - 2
• o conjunto das raizes será S = {- 2, 4}
João Marcos Ferreira

21. Passemos agora para a resolução
de alguns exercicios
• Espero que todos tenham aproveitado esta
• rápida aula. As anotações são importantes
• para o caso de precisarem rever o assunto
• Obrigado pela audiência.
• Prof. Demerval Dias Miranda
João Marcos Ferreira