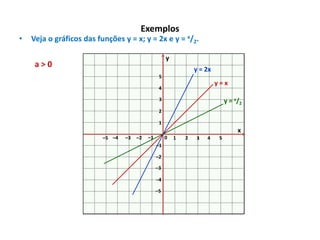
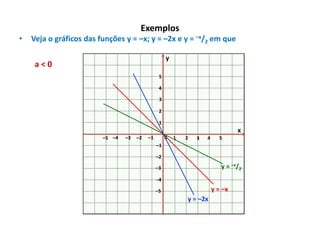
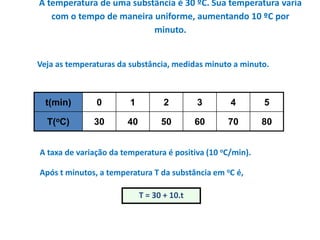
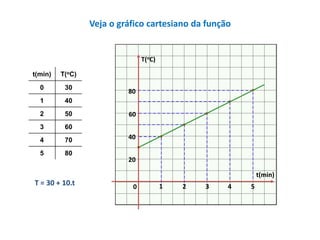
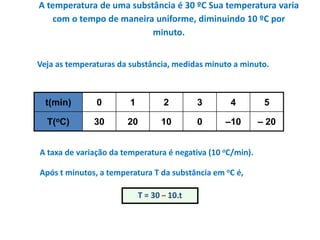
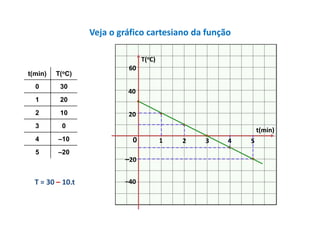
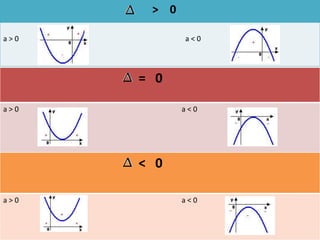
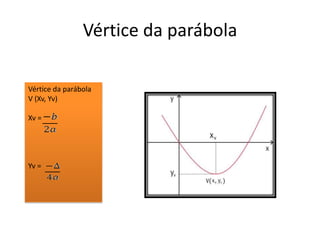
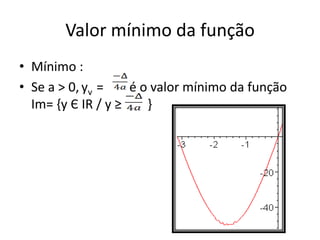
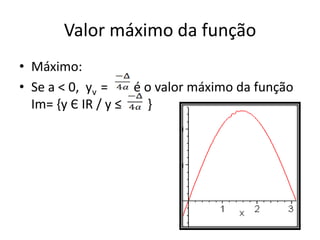
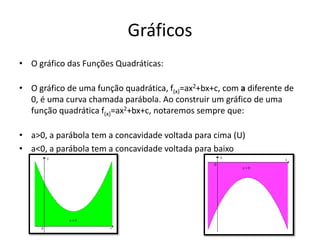
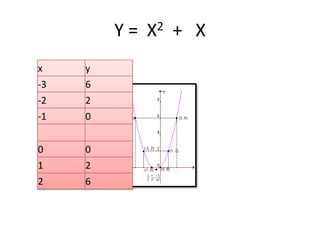
O documento apresenta um resumo sobre equações de segundo grau. Define o que é uma equação de segundo grau e explica os conceitos de coeficientes, raízes, equações completas e incompletas. Apresenta exemplos e atividades sobre identificação de coeficientes e resolução de equações.

1. Escola municipal são José
• Prof:Zaqueu Oliveira
• Revisão geral

2. Equações do 2º Grau
2
ax
+ bx + c = 0, a ≠ 0

3. Definição:
Denomina-se equação do 2º grau, na incógnita x, toda
equação da forma: ax2 + bx + c = 0, a ≠ 0.
Observe que:
a representa o coeficiente de x²;
b representa o coeficiente de x;
c representa o termo independente.
Exemplos:
x2 - 5x + 6 = 0, onde a = 1, b = -5 e c = 6.
2 - x = 0, onde a = 7, b = -1 e c = 0.
7x
x2 - 36 = 0, onde a = 1, b = 0 e c = -36.

4. Equações Completas do 2º Grau
Uma equação do 2º grau é completa quando b e c são
diferentes de zero.
Exemplos:
x² - 9x + 20 = 0, onde a = 1, b = -9 e c = 20.
-x² + 10x - 16 = 0, onde a = -1, b = 10 e c = -16.

5. Equações Incompletas do 2º Grau
Uma equação do 2º grau é incompleta quando b ou c é
igual a zero, ou ainda, quando ambos são iguais a zero.
Equações da forma ax² +bx = 0, (c = 0)
x² - 3x = 0, onde a = 1, b = -3.
-2x² + 4x = 0, onde a = -2, b = 4.
Equações da forma ax² +c = 0, (b = 0)
3x² - 2 = 0, onde a = 3, c = -2.
x² + 5 = 0, onde a = 1, c = 5.

6. ATIVIDADE-1
1. Obtenha os coeficientes
equações do 2 grau:
a) 5x²-7x-3=0
a:5 b:-7
b) x²-4x +2=0
a:1
b:-4
c) x²-x-1=0
a:1 b:-1
d) 2x²+7x+8=0 a:2 b:7
e) x²-7x=0
a:1 b:-7
f) x²-25=0
a:1
b:0
das
c:-3
c:2
c:-1
c:8
c:0
c:-25

7. 2. Forme as equações do 2° grau em x:
•
a=1;
x²-6x+5=0
b=-6 ;
c= 5
b) a=3;
b=7 ;
3x²+7x+8=0
c= 8
c) a=8;
8x²=0
c=0
b=0 ;
d) a=1;
b=-3 ;
x²-3x+4=0
c= 4

8. Resolução de Equações Incompletas
Equações da forma:
ax² +bx = 0, (c = 0)
Equações da forma:
ax² +c = 0, (b = 0)
De modo geral, a equação
do tipo ax² +bx = 0 tem
para soluções:
De modo geral, a equação
do tipo ax² +c = 0:
x=0
e
x=-b
a
possui duas raízes reais se:
- c for um nº positivo
a
não possui raiz real se:
- c for um nº negativo
a

9. ATIVIDADE-2
1.Determine o conjunto verdade das equações:
x²-7x = 0 Δ=b²-4.a.c x=7+7=14/2=7
Δ=7²-4.1.0
Δ=49
x=7-7=0/2=0
b) 3x²-6x = 0
Δ=b²-4.a.c
Δ=-6²-4.3.0
Δ=36
x=6+6=12/6=2
x=6-6=0/2=0
Δ=b²-4.a.c
Δ=5²-4.1.0
Δ=25
x=-5+5=0/2=0
x=-5-5=-10/2=-5
c) x² +5x = 0

10. 2.Determine o conjunto verdade das equações:
X² - 49 = 0 a=1 Δ=0²-4.1.49 x=14/2=7
Δ=196
2x² -32 = 0 Δ=0²-4.2.32
x=16/4 =4
Δ= 0+256
Δ=256
5x² - 20 = 0
Δ=0²-4.5.-20
Δ=400
x= 0+20=20/10=2

11. Composição de uma Equação do
2º Grau, Conhecidas as Raízes
Considere a equação do 2º grau ax2 + bx + c = 0.
Dividindo todos os termos por a, a ≠ 0, obtemos:
ax2 + bx + c = 0
a
a
a
x2 + bx + c = 0
a
a
Como: S = x’+ x” = -b e P = x’. x” = c
a
a
Podemos escrever a equação desta maneira:
x2 - Sx + P = 0

12. Exercício sobre Composição
Componha a equação do 2º grau cujas raízes são -2 e 7.
Solução:
A soma das raízes corresponde a:
S = x1 + x2 = -2 + 7 = 5
O produto das raízes corresponde a:
P = x1 . x2 = ( -2) . 7 = -14
A equação é dada por x2 - Sx + P = 0, onde S = 5 e P = -14.
Logo, x2 - 5x - 14 = 0 é a equação procurada.

13. ATIVIDADE – 4
Componha a equação do 2º grau cujas raízes são:
•
•
•
•
•
•
•
•
•
•
•
•
5 e2
R=x²-sx+p=0
x²-7x+10=0
-2 e -3
R= x²-sx+p=0
x²+5x-6=0
4 e -5
R=x²-sx+p=0
x²+1x - 20=0 => x² + x – 20 = 0
-5 e 5
R= x² -sx+p=0
x²-25=0

14. Representação gráfica de função
1º grau

15. Função de 1º grau é toda função do tipo
y = f(x) = ax + b
Em que a e b são constantes reais, com a ≠ 0.
Se b = 0, temos a função y = f(x) = ax, chamada, também, função linear.

16. Características da função de 1º grau y = f(x) = ax + b.
• A fórmula que a define é um polinômio de 1º grau; seu termo
independente pode ser nulo ou não.
• Se b = 0, temos a função f(x) = ax, chamada de função linear.
• A constante real a, não-nula, é o coeficiente angular. Ela é a mesma,
qualquer que seja o intervalo considerado.

17. Características da função de 1º grau y = f(x) = ax + b.
• A constante real b é o coeficiente linear.
• Seu gráfico cartesiano é uma linha reta, não paralela aos eixos. Ela
pode conter a origem (caso b = 0) ou não conter origem (caso b ≠
0).
• O crescimento ou o decrescimento da função estão relacionados
com o sinal de a. A reta é ascendente para a > 0 e descendente
para a < 0.

18. Crescimento e decrescimento.
a > 0 ⇒ função crescente
⇒ reta ascendente (sobe da esquerda p/ direita)
a < 0 ⇒ função decrescente
⇒
reta descendente (desce da esquerda p/ direita)

19. •
Exemplos
Veja o gráficos das funções y = x; y = 2x e y = x/2.
y
a>0
y = 2x
5
y=x
4
3
y = x/2
2
1
x
–5 –4
–3
–2
–1
0
–1
–2
–3
–4
–5
1
2
3
4
5

20. Exemplos
•
Veja o gráficos das funções y = –x; y = –2x e y = –x/2 em que
y
a<0
5
4
3
2
1
x
–5 –4
–3
–2
–1
0
1
2
3
4
5
–1
–2
y = –x/2
–3
–4
y = –x
–5
y = –2x

21. A temperatura de uma substância é 30 ºC. Sua temperatura varia
com o tempo de maneira uniforme, aumentando 10 ºC por
minuto.
Veja as temperaturas da substância, medidas minuto a minuto.
t(min)
0
1
2
3
4
5
T(oC)
30
40
50
60
70
80
A taxa de variação da temperatura é positiva (10 oC/min).
Após t minutos, a temperatura T da substância em oC é,
T = 30 + 10.t

22. Veja o gráfico cartesiano da função
T(oC)
t(min)
T(oC)
0
30
1
40
2
50
3
60
4
70
5
80
80
60
40
20
t(min)
T = 30 + 10.t
0
1
2
3
4
5

23. A temperatura de uma substância é 30 ºC Sua temperatura varia
com o tempo de maneira uniforme, diminuindo 10 ºC por
minuto.
Veja as temperaturas da substância, medidas minuto a minuto.
t(min)
0
1
2
3
4
5
T(oC)
30
20
10
0
–10
– 20
A taxa de variação da temperatura é negativa (10 oC/min).
Após t minutos, a temperatura T da substância em oC é,
T = 30 – 10.t

24. Veja o gráfico cartesiano da função
T(oC)
t(min)
T(oC)
0
30
1
20
2
10
3
0
4
–10
5
60
–20
40
20
t(min)
0
–20
T = 30 – 10.t
–40
1
2
3
4
5

26. Definição
Chama-se função quadrática, ou função
polinomial do 2º grau, qualquer função f de IR em
IR dada por uma lei da forma f(x) = ax2 + bx + c,
onde a, b e c são números reais e a 0.
Vejamos alguns exemplos de função quadráticas:
f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2 -1, onde a = 1, b = 0 e c = -1
f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
f(x) = -4x2, onde a = - 4, b = 0 e c = 0

27. Pontos notáveis da parábola
Os pontos de interseção com o eixo Ox (se
existirem)
Para resolvê-la, utilizamos a fórmula de
Bhaskara :
 x=
em que,
2
Se > 0 , temos duas reízes reais
distintas.
Se < 0 , não temos raízes reais.
Se = 0 , temos duas raízes reais e iguais.

28. > 0
a>0
a<0
= 0
a>0
a<0
< 0
a>0
a<0

29. Raízes ou zeros da função
• Denominam-se zeros ou raízes de uma função
de 2° grau os valores de x que anulam a
função, ou seja, que tornam f(x)=0
• As raízes da função nada mais é onde a
parábola corta no eixo do x.

30. Vértice da parábola
Vértice da parábola
V (Xv, Yv)
Xv =
Yv =

31. Raízes ou zeros da função
• Denominam-se zeros ou raízes de uma função
de 2° grau os valores de x que anulam a
função, ou seja, que tornam f(x)=0
• As raízes da função nada mais é onde a
parábola corta no eixo do x.

32. Valor mínimo da função
• Mínimo :
• Se a > 0, yv =
é o valor mínimo da função
Im= {y Є IR / y ≥
}

33. Valor máximo da função
• Máximo:
• Se a < 0, yv =
é o valor máximo da função
Im= {y Є IR / y ≤
}

34. EXEMPLO:
Estudar o sinal da função f(x)= x2 - 5x + 6.
x2 - 5x + 6 = 0 (determina-se a raiz da função)
(marcam-se as raízes em uma reta e analisa-se
a concavidade da parábola)
(faz-se o estudo do sinal)
f(x) > 0, para x<2 ou x>3
f(x)=0, para x=2 ou x=3
f(x) < 0, para 2 < x < 3

35. Gráficos
• O gráfico das Funções Quadráticas:
• O gráfico de uma função quadrática, f(x)=ax2+bx+c, com a diferente de
0, é uma curva chamada parábola. Ao construir um gráfico de uma
função quadrática f(x)=ax2+bx+c, notaremos sempre que:
• a>0, a parábola tem a concavidade voltada para cima (U)
• a<0, a parábola tem a concavidade voltada para baixo

36. Y = X2 + X
x
-3
-2
-1
y
6
2
0
0
1
2
0
2
6

37. 1.RAZÃO
Arazão de dois números a e b, com b 0, é o quociente
do primeiro pelo segundo:
OBSERVAÇÃO:
Apalavra razão vem do latim ratio, que
significa divisão.
Exemplos

38. 2.RAZÃO DE DOIS SEGMENTOS
Chamamos razão de dois segmentos a razão ou quociente
entre os números que exprimem as medidas desses
segmentos, tomados na mesma unidade.
Exemplos:
Determinar a razão entre os segmentos AB e CD, sendo
AB = 6 cm e CD = 12 cm.(Lembre-se :AB representa a
medida do segmento AB.)

39. Exemplos:
1) Verifique se os segmentosAB =4 cm, CD = 6 cm, EF =
8 cm e GH = 12 cm formam, nessa ordem, uma proporção.
Podemos afirmar que os segmentos, nessa ordem, são
proporcionais.

40. 3.SEGMENTOS PROPORCIONAIS
Dizemos que quatro segmentos, AB, CD, EF e GH, nessa
ordem, são proporcionais, quando a razão entre os dois
primeiros for igual à razão entre os dois últimos, ou
seja:AB, CD, EF e GH são, nessa ordem, proporcionais
se, e somente se:

41. 2) Verifique se os segmentos AB = 7 cm, CD = 10cm, EF =
12 cm e GH = 5 cm formam, nessa ordem, uma proporção.
Podemos afirmar que os segmentos, nessa ordem, não são
proporcionais.

42. 3) Quatro segmentos AB, MN, PQ e RS, nesta ordem, são
proporcionais. SeAB=5 cm, MN= 15 cm e PQ= 4 cm, qual
a medida de RS?
5x = 60
x= 12

43. Que tal você tentar resolver o
Problema abaixo usando a relação
Entre as alturas propostas por Tales
1) (Saresp) Um prédio projeta uma sombra de 40 m ao mesmo
tempo que um poste de 2 m projeta uma sombra de 5 m.
Então, a altura do prédio é
A)
B)
C)
D)
10 m.
12 m.
14 m.
16 m.