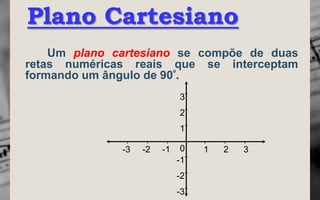
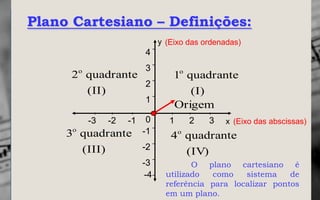
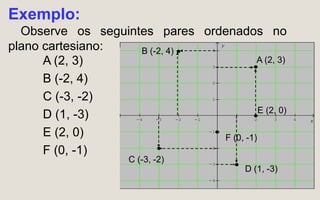
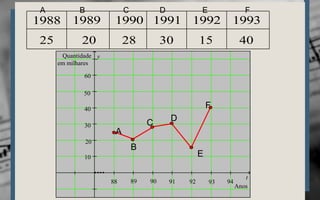
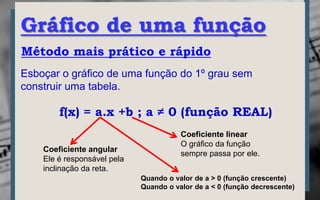
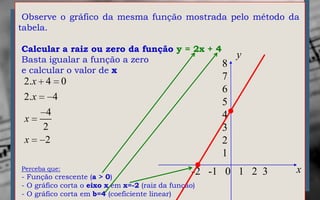
O documento explica os conceitos básicos de plano cartesiano, pares ordenados e como construir gráficos de funções do primeiro grau através de tabelas de valores ou diretamente a partir da equação da função. É apresentado um exemplo numérico de vendas de carros por ano para ilustrar a construção de um gráfico no plano cartesiano.

3. Plano Cartesiano
Um plano cartesiano se compõe de duas
retas numéricas reais que se interceptam
formando um ângulo de 90º.
3
2
1
-3 -2 -1 0 1 2 3
-1
-2
-3

4. Plano Cartesiano – Definições:
y (Eixo das ordenadas)
4
o 3
2 quadrante 1o quadrante
2
(II) (I)
1
Origem
-3 -2 -1 0 1 2 3 x (Eixo das abscissas)
3o quadrante -1
4o quadrante
(III) -2
(IV)
-3 O plano cartesiano é
-4 utilizado como sistema de
referência para localizar pontos
em um plano.

6. Pares Ordenados
O par ordenado é um par de números na forma
(x, y) em que a ordem dos números é importante.
A forma geral de um par ordenado é:
(abscissa, ordenada)
( x , y )
Cada par ordenado representa um ponto no plano
cartesiano e vice-versa.

7. Exemplo:
Observe os seguintes pares ordenados no
plano cartesiano: B (-2, 4)
y
4
A (2, 3) A (2, 3)
3
B (-2, 4) 2
C (-3, -2) 1
E (2, 0)
D (1, -3) -4 -3 -2 -1 1 2 3 4 x
E (2, 0) F (0, -1)
-1
F (0, -1) -2
C (-3, -2) -3
D (1, -3)
-4

8. Aplicação :
A quantidade (em milhares) de
automóveis vendidos em Mossoró
nos anos de 1988 a 1993 está
representada na tabela:
Ano 1988 1989 1990 1991 1992 1993
Carros 25 20 28 30 15 40

9. Localizando os pontos no
plano cartesiano.
O gráfico será obtido unindo
os pontos com segmentos de
retas.

10. A B C D E F
1988 1989 1990 1991 1992 1993
25 20 28 30 15 40
Quantidade y
em milhares
60
50
40 F
C D
30 AA
20
B
10 E
t
88 89 90 91 92 93 94
Anos

11. Gráfico de uma função
Método usando tabela de valores
Para esboçar o gráfico de uma função
do 1º grau no plano cartesiano,
devemos atribuir valores a x,
determinando os respectivos valores
numéricos de y (fazendo uma tabela).

12. Exemplo:
Veja a função abaixo.
y = 2x +4 ou f(x) = 2x + 4
1o) Fazer uma tabela:
x y = 2x+4 y (x, y)
-2 y = 2.(-2)+4 y = -4 + 4 = 0 (-2, 0)
-1 y = 2.(-1) + 4 y = -2 + 4 = 2 (-1, 2)
0 y = 2.0 + 4 y=0+4=4 (0, 4)
1 y = 2.1 + 4 y=2+4=6 (1, 6)
2 y = 2.2 + 4 y=4+4=8 (2, 8)

13. 2o) Colocar os pontos num plano cartesiano;
3o) Unir os pontos. y = 2x + 4
y TABELA
8 (x, y)
7
6 (-2, 0)
5 (-1, 2)
4
(0, 4)
3
2 (1, 6)
1 (2, 8)
-2 -1 0 1 2 3 x
O gráfico de uma função do 1º grau
é sempre uma reta

14. Gráfico de uma função
Método mais prático e rápido
Esboçar o gráfico de uma função do 1º grau sem
construir uma tabela.
f(x) = a.x +b ; a ≠ 0 (função REAL)
Coeficiente linear
O gráfico da função
Coeficiente angular
sempre passa por ele.
Ele é responsável pela
inclinação da reta.
Quando o valor de a > 0 (função crescente)
Quando o valor de a < 0 (função decrescente)

15. Observe o gráfico da mesma função mostrada pelo método da
tabela.
Calcular a raiz ou zero da função y = 2x + 4
Basta igualar a função a zero
y
8
e calcular o valor de x
2.x 4 0 7
6
2.x 4
5
4 4
x
2 3
x 2 2
1
Perceba que: x
- Função crescente (a > 0)
-2 -1 0 1 2 3
- O gráfico corta o eixo x em x=-2 (raiz da função)
- O gráfico corta em b=4 (coeficiente linear)

16. Agora vamos exercitar:
Aplique o que aprendeu nessa aula,
resolvendo as questões propostas a seguir.
Pois seu concorrente já começou a resolver!
Bons estudos!

17. Construa o gráfico das seguintes
funções do 1º grau.

18. Fim.