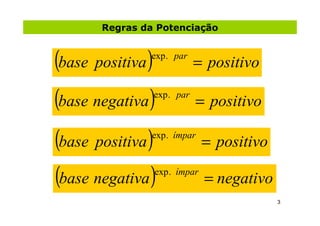
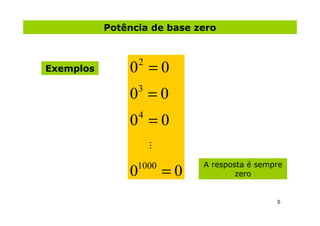
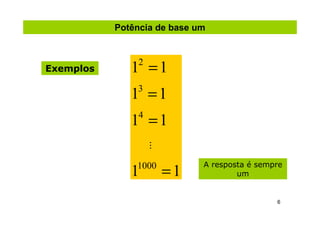
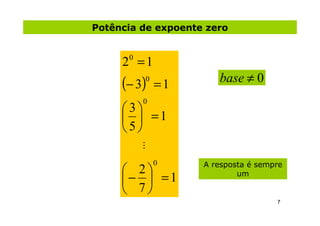
1) O documento apresenta as regras e propriedades da potenciação, incluindo o comportamento da base quando o expoente é par/ímpar, positivo/negativo ou zero. 2) São mostrados exemplos de cálculos de potenciação para diferentes bases e expoentes. 3) As propriedades operatórias de potenciação, como soma e multiplicação de expoentes para mesma base, são explicadas.

1. Aula 3 – 24/03/2011
Prof. Paulo Berndt 1

2. Potenciação
2

3. Regras da Potenciação
(base positiva )
exp . par
= positivo
(base negativa ) exp . par
= positivo
(base positiva )exp . ímpar
= positivo
(base negativa ) exp . ímpar
= negativo
3

4. Exemplos de Potenciação
(+ 2) 5
= +32 (+ 2) 2
= +4
(− 3) 3
= −27 (− 3) 2
= +9
Cuidado: se não há
parêntesis significa
que o sinal negativo − 5 = −25
2
não está sendo
elevado ao quadrado 4

5. Potência de base zero
Exemplos 0 =02
0 =03
0 =04
...
=0
1000 A resposta é sempre
0 zero
5

6. Potência de base um
Exemplos 1 =1
2
1 =1
3
1 =1
4
...
=1
1000 A resposta é sempre
1 um
6

7. Potência de expoente zero
2 =1
0
(− 3) 0
=1 base ≠ 0
0
3
  =1
5
...
0 A resposta é sempre
 2
−  =1 um
 7
7

8. Potência de expoente um
2 =2
1
(− 3)1
= −3
1
3 3
  =
5 5
...
1 A resposta é sempre
 2 2
−  = − a própria base
 7 7
8

9. Potência de expoente negativo
Exemplos:
−n n
a b −2
= 
2
2 3
 
9
  =  =
3 2 4
b a  2
− 
−2
 3
= −  =
9
2
 3  2 4
Inverte-se a base e 3
 1
troca-se o sinal do
expoente. (− 5)
−3
= −  = −
1
 5 125
−3 3
 1  2
 −  =  −  = (− 2) = −8
3
 2  1
9

10. Propriedades Operatórias das Potências
m+ n
a ⋅a = a
m n Multiplicação de
potências de mesma
base: somam-se os
expoentes
m−n
a ÷a = a
Divisão de potências
m n de mesma base:
subtraem-se os
expoentes
(a )
Potência de potência:
m n m⋅ n
=a
multiplicam-se os
expoentes
10

11. Propriedades Operatórias - Exemplos
Exemplos
(− 2) ⋅ (− 2)
3 7
= (− 2 ) = +1024
10
13 9 4
3 3 3 81
  ÷  =   =
4 4 4 256
[(− 2) ] = (− 2)
3 4 12
= +4096 11

12. Questão de Prova – Regras de Potências
→ −(− 2 ) = −(+ 1) = −1 → Verdadeiro
0
→ −2 2 = −4 e − (− 2) = −(+ 4) = −4 → Verdadeiro
2
→ −(− 2 ) = −(− 8) = +8 e 23 = +8 → Verdadeiro
3
→ (− 2)0 = +1 e − (− 2 ) = −(+ 1) = −1 → Falso
0
12

13. Questão de Prova – Regras de potências
x − x + x = (− 1) − (− 1) + (− 1)
3 47 48 3 47 48
= −1 − (− 1) + (+ 1)
= −1 + 1 + 1
= −1 + 2
=1
13

14. Questão de Prova – Propriedades das potências
(A) 625 5
125 5
Substituindo x por 5 y
25 5
(5 )
y 2
+ 625 = 52 y + 4 5 5
1
52 y + 54 = 52 y + 4 → Falso
a n ⋅ a m = a n + m → Multiplicação de pot. de mesma base
52 y ⋅ 54 = 52 y + 4 → Assim estaria correto!
14