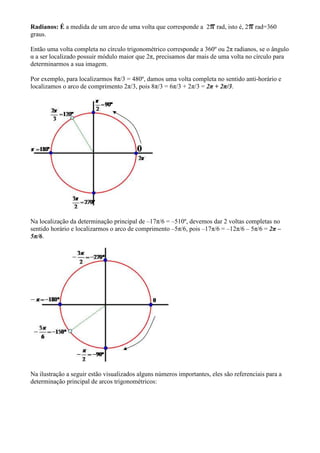
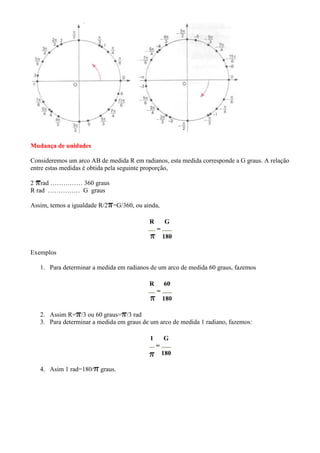
1) O documento discute trigonometria no triângulo retângulo e na circunferência, definindo termos como seno, cosseno e tangente. 2) É apresentado o Teorema de Pitágoras para triângulos retângulos e as funções trigonométricas básicas. 3) As unidades de medida de arcos como radianos e graus são explicadas, assim como a relação entre elas.

1. TRIGONOMETRIA
Triângulo Retângulo
É um triângulo que possui um dos seus ângulos medindo noventa graus, ou seja, possui um ângulo
reto, daí o nome triângulo retângulo. Como a soma das medidas dos ângulos internos de um
triângulo é igual a 180 graus, então os outros dois ângulos medirão 90 graus.
Observação: Quando a soma de dois ângulos mede 90 graus, estes ângulos são denominados
complementares, portanto podemos dizer que o triângulo retângulo possui dois ângulos
complementares.
Lados de um triângulo retângulo
Os lados de um triângulo retângulo recebem nomes especiais. Estes nomes são dados de acordo
com a posição em relação ao ângulo reto. O lado oposto ao ângulo reto é a hipotenusa. Os lados que
formam o ângulo reto (adjacentes a ele) são os catetos.
Palavras Cateto Cathetós:(perpendicular)
gregas Hipotenusa Hypoteinusa:Hypó(por baixo) + teino(eu estendo)
Para padronizar o estudo da Trigonometria, adotaremos as seguintes notações:
Letra Lado Letra Vértice e Ângulo
a Hipotenusa (BC) A Ângulo reto (A=90o)
b Cateto (AC) B Ângulo agudo (B<90o)
c Cateto (AB) C Ângulo agudo (C<90o)
Nomenclatura dos catetos
Os catetos recebem nomes especiais de acordo com a sua posição em relação ao ângulo sob análise.
Se estivermos operando com o ângulo C, então o lado oposto, indicado por c, é o cateto oposto ao
ângulo C e o lado adjacente ao ângulo C, indicado por b, é o cateto adjacente ao ângulo C.
Ângulo Lado oposto Lado adjacente
C c (cateto oposto) b (cateto adjacente)
B b (cateto oposto) c (cateto adjacente)
Um dos objetivos da trigonometria é mostrar a utilidade do conceitos matemáticos no nosso
cotidiano. Iniciaremos estudando as propriedades geométricas e trigonométricas no triângulo
retângulo. O estudo da trigonometria é extenso e minucioso.
Teorema de Pitágoras
Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos
quadrados das medidas dos catetos.

2. Isso significa que, conhecendo as medidas de dois lados de um triângulo retângulo, pode-se calcular
a medida do terceiro lado — propriedade única dos triângulos retângulos
Funções trigonométricas básicas
As Funções trigonométricas básicas são relações entre as medidas dos lados do triângulo retângulo
e seus ângulos. As três funções básicas mais importantes da trigonometria são: seno, cosseno e
tangente. O ângulo será indicado pela letra x.
Função Notação Definição
seno sen(x) medida do cateto oposto a x / medida da hipotenusa
cosseno cos(x) medida do cateto adjacente a x / medida da hipotenusa
tangente tg(x) medida do cateto oposto a x / medida do cateto adjacente a x
Se tomarmos um triângulo retângulo ABC, com hipotenusa igual a 1 (uma) unidade de medida,
então o seno do ângulo sob análise será o seu cateto oposto, e o cosseno do mesmo, será o seu
cateto adjacente. Portanto a tangente do ângulo analisado será a razão entre seno e cosseno do
mesmo ângulo.
1 – Trigonometria no triângulo retângulo
A palavra trigonometria significa medida dos três ângulos de um triângulo e determina um ramo da
matemática que estuda a relação entre as mediadas dos lados e dos ângulos de um triângulo.
Conta a história da matemática que Tales foi um grande estudioso desse ramo da matemática, mas
não podemos afirmar que este foi seu inventor. A trigonometria não foi obra de um só homem, nem
de um povo só.
Seno, Cosseno e Tangente de um Ângulo Agudo
Observe o triângulo retângulo abaixo, onde a é a hipotenusa (lado oposto ao ângulo de 90º), b e c
são os catetos do triângulo retângulo (catetos são os lados que formam o ângulo de 90º). Lembre-se,
os catetos variam de nome de acordo com a posição do ângulo.

3. Valores especiais:
Considere-se o seguinte triângulo escaleno. Observando a figura vem:
Considere-se o seguinte triângulo isósceles, tendo os catetos uma unidade de comprimento:
Em resumo, tem-se:

4. 2- Trigonometria na Circunferência
A circunferência trigonométrica está representada no plano cartesiano com raio medindo uma
unidade. Ela possui dois sentidos a partir de um ponto A qualquer, escolhido como a origem dos
arcos. O ponto A será localizado na abscissa do eixo de coordenadas cartesianas, dessa forma, este
ponto terá abscissa 1 e ordenada 0. Os eixos do plano cartesiano dividem o círculo trigonométrico
em quatro partes, chamadas de quadrantes.
Ponto móvel sobre uma curva
Consideremos uma curva no plano cartesiano. Se um ponto P está localizado sobre esta curva,
simplesmente dizemos P pertence à curva e que P é um ponto fixo na mesma. Se assumirmos que
este ponto possa ser deslocado sobre a curva, este ponto receberá o nome de ponto móvel.
Um ponto móvel localizado sobre uma circunferência, partindo de um ponto A pode percorrer esta
circunferência em dois sentidos opostos. Por convenção, o sentido anti-horário (contrário aos
ponteiros de um relógio) é adotado como sentido positivo
Arcos da circunferência
Se um ponto móvel em uma circunferência partir de A e parar em M, ele descreve um arco AM. O
ponto A é a origem do arco e M é a extremidade do arco.
Quando escolhemos um dos sentidos de percurso, o arco é denominado arco orientado e
simplesmente pode ser denotado por AB se o sentido de percurso for de A para B e BA quando o
sentido de percurso for de B para A.
Quando não consideramos a orientação dos arcos formados por dois pontos A e B sobre uma
circunferência, temos dois arcos não orientados sendo A e B as suas extremidades.
Medida de um arco
A medida de um arco de circunferência é feita por comparação com um outro arco da mesma
circunferência tomado como a unidade de arco. Se u for um arco de comprimento unitário (igual a
1), a medida do arco AB, é o número de vezes que o arco u cabe no arco AB.
Na figura em anexo, a medida do arco AB é 5 vezes a medida do arco u. Denotando a medida do
arco AB por m(AB) e a medida do arco u por m(u), temos m(AB)=5 m(u).

5. A medida de um arco de circunferência é a mesma em qualquer um dos sentidos. A medida
algébrica de um arco AB desta circunferência, é o comprimento deste arco, associado a um sinal
positivo se o sentido de A para B for anti-horário, e negativo se o sentido for
horário.
O número pi
Para toda circunferência, a razão entre o perímetro e o diâmetro é constante. Esta constante é
denotada pela letra grega , que é um número irracional, isto é, não pode ser expresso como a
divisão de dois números inteiros. Uma aproximação para o número é dada por:
= 3,1415926535897932384626433832795…
Unidades de medida de arcos
A unidade de medida de arco do Sistema Internacional (SI) é o radiano, mas existem outras
medidas utilizadas pelos técnicos que são o grau e o grado. Este último não é muito comum.
Radiano: Medida de um arco que tem o mesmo comprimento que o raio da circunferência na qual
estamos medindo o arco. Assim o arco tomado como unidade tem comprimento igual ao
comprimento do raio ou 1 radiano, que denotaremos por 1 rad.
Grau: Medida de um arco que corresponde a 1/360 do arco completo da circunferência na qual
estamos medindo o arco.

6. Radianos: É a medida de um arco de uma volta que corresponde a 2 rad, isto é, 2 rad=360
graus.
Então uma volta completa no círculo trigonométrico corresponde a 360º ou 2π radianos, se o ângulo
α a ser localizado possuir módulo maior que 2π, precisamos dar mais de uma volta no círculo para
determinarmos a sua imagem.
Por exemplo, para localizarmos 8π/3 = 480º, damos uma volta completa no sentido anti-horário e
localizamos o arco de comprimento 2π/3, pois 8π/3 = 6π/3 + 2π/3 = 2π + 2π/3.
Na localização da determinação principal de –17π/6 = –510º, devemos dar 2 voltas completas no
sentido horário e localizarmos o arco de comprimento –5π/6, pois –17π/6 = –12π/6 – 5π/6 = 2π –
5π/6.
Na ilustração a seguir estão visualizados alguns números importantes, eles são referenciais para a
determinação principal de arcos trigonométricos:

7. Mudança de unidades
Consideremos um arco AB de medida R em radianos, esta medida corresponde a G graus. A relação
entre estas medidas é obtida pela seguinte proporção,
2 rad …………… 360 graus
R rad …………… G graus
Assim, temos a igualdade R/2 =G/360, ou ainda,
R G
=
180
Exemplos
1. Para determinar a medida em radianos de um arco de medida 60 graus, fazemos
R 60
=
180
2. Assim R= /3 ou 60 graus= /3 rad
3. Para determinar a medida em graus de um arco de medida 1 radiano, fazemos:
1 G
=
180
4. Asim 1 rad=180/ graus.