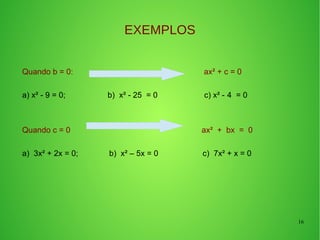Este documento fornece uma introdução às equações de segundo grau, incluindo: (1) Definição de equação de segundo grau e sua forma geral; (2) Exemplos de equações de segundo grau completas e incompletas; (3) Métodos para encontrar as raízes de equações de segundo grau incompletas e completas.

1. EQUAÇÃO DO 2° GRAUEQUAÇÃO DO 2° GRAU
Descritores:Descritores:
- Identificar uma equação do 2° grau- Identificar uma equação do 2° grau
(completa e incompleta).(completa e incompleta).
- Resolver uma equação do 2° grau- Resolver uma equação do 2° grau
incompleta .incompleta .
- Verificar se um determinado número é- Verificar se um determinado número é
ou não raiz de uma equação do 2° grau.ou não raiz de uma equação do 2° grau.

2. Equação do 2° grauEquação do 2° grau
O que é equação ?
O que é equação do 2° grau?

3. 3
Temos que observar o expoente...
Equação é uma sentença matemática (afirmação que envolve
raciocínio matemático) que apresenta uma igualdade, além de
um termo desconhecido representado por uma letra minúscula.
x + 3 = 10
Nesse caso a letra x representa o número 7.
Observe que o x está elevado a 1: (x¹)
Nesse caso temos uma equação do primeiro grau.
Vejamos outros exemplos:
a) 3x + 8 – x = -4x + 8
b) 3(x + 1) = -4 + 8x
●
●
●

4. 4
E quando o x está elevado a 2?
Nesse caso teremos uma equação do 2° grau.
Exemplos:
a)x² – 9 = 0
b) 2x² -10x + 12 = 0
é claro que se a variável estiver elevada a 3 teremos uma equação do
terceiro grau e assim por diante.
●

5. 5
Atividade:
(copie e responda no caderno)
Assinale o item que apresenta equação do segundo grau:
a) 2x + 5 = 0
b) x² + 5 = 0
c) x³ + 8 = x² – 1
d) 2x³ + x² – 8 = 0
e) 5x + 4 = x² – 8
f) 3x – 2(x + 5) = -8
g) (x+ 1).(x – 1) = 0
h) 5x² + 2x = 0
i) (x + 3 )² = 0

6. 6
Equação do segundo grau
completa e incompleta
Forma geral da equação do segundo grau:
ax² +bx + c = 0
A letra “a” representa um número racional que é
chamado de coeficiente de x²
A letra “b” representa um número racional que é
chamado de coeficiente de x, e
A letra “c” representa um número racional que é
chamado de termo independente.

7. 7
Vamos observar alguns exemplos?
a) x² - 4x + 3 = 0
b) x² - 5x + 6 = 0
c) 3x² - 5x + 3 = 0
2 2
d) x² + 2x – 8 = 0
ATIVIDADE: Identifique os coeficientes numéricos
das equações do segundo grau
acima.

8. 8
ax² + bx + c = 0
Um detalhe importante!
Nem sempre você vai encontrar as equações
tão “arrumadinhas” assim, isto é, escritas na
forma geral

9. 9
Vejamos:
x² - 3x = -8
-5x = -x² – 6
2x – 4 = 3x²
Você consegue identificar os coeficientes
das equações acima? Aposto que sim!
●
●

10. 10
O que é “raiz de uma equação”?
● É o valor que podemos atribuir a x de modo que a igualdade se
torne verdadeira.
● Vejamos numa equação do 1° grau:
● a) x + 5 = 17, nesse caso a raiz é o número 12, já que 12 + 5 =
17
● b) 3x + 8 = -7, aqui o valor de x é -5, pois
3.(-5) + 8 = -7
Você entendeu?Você entendeu?
Então agora é com você: qual a raiz da equaçãoEntão agora é com você: qual a raiz da equação
5x + 3 = 13?5x + 3 = 13?
●
●

11. 11
Da mesma forma, raiz da equação do 2°
grau segue o mesmo raciocínio.
● Observe a equação x² -5x + 6 = 0
● Qual(is) seria(m) o(s) valor (es) atribuído(s) a x que torna(m) a
igualdade verdadeira?
Se x = 2, teremos: (2²) – 5. (2) + 6 = 0
Agora é só fazer contas...
2² – 5.2 + 6 = 0
4 – 10 + 6 = 0
-6 + 6 = 0, daí vemos que 0 = 0 (verdadeiro), portanto 2 é uma
raiz dessa equação.

12. 12
Mas...Mas...
equação do 2° grau tem duas raízes?equação do 2° grau tem duas raízes?
SIM ! ! !
Na equação anterior o número 3 também é raiz. Veja:
x² – 5x + 6 = 0, sendo x = 3, teremos:
3² – 5.3 + 6 = 0, daí vem:
9 – 15 + 6 = 0
-6 + 6 = 0
0 = 0 (verdadeiro), logo 3 é raiz da equação.

13. 13
Exemplo de número que não é
raiz...
● Na equação anterior podemos observar que
4 não é raiz.
x² -5x + 6 = 0, sendo x = 4, teremos:
4² – 5.3 + 6 = 0
16 – 15 + 6 = 0
-1 + 6 = 0, tem sentido dizer que +5 = 0?
Claro que não, portanto, 4 não é raiz dessa
equação.

14. 14
ATIVIDADES:
1) Verifique se os números abaixo são raízes da
equação x² – 4x + 3 = 0
a) 3
b) 6
c) -4
d) 0
e) 2
f) 1
●
●

15. 15
2) -4 é raiz da equação x² + 3x -4 = 0 ?
● Como obter as raízes de uma equação do
segundo grau?
● Vamos separar as equações em dois tipos:
●
COMPLETA E INCOMPLETA.COMPLETA E INCOMPLETA.
Considerando a forma geral ax² + bx + c = 0
quando b = 0 vem: ax² + bx = 0
● Quando c = 0, temos: ax² + c = 0
●
●

16. 16
EXEMPLOS
Quando b = 0: ax² + c = 0
a) x² - 9 = 0; b) x² - 25 = 0 c) x² - 4 = 0
Quando c = 0 ax² + bx = 0
a) 3x² + 2x = 0; b) x² – 5x = 0 c) 7x² + x = 0

17. 17
● Vamos aprender a encontrar as raízes da equação
do 2° incompleta do tipo =ax² + c = 0 ?
● OBS.: Resolver uma equação é encontrar as raízesResolver uma equação é encontrar as raízes
dessa equação.dessa equação.
Exemplos:
● a) x² – 9 = 0
x² = 0 + 9 (“colocando” o 9 no 2° membro)
x² = 9, daí teremos: x = √9
x = ± 3, ou seja, as raízes são os números -3 e +3.
Conjunto solução: S = { -3, +3 }
●

18. 18
● b) x² – 16 = 0
Resolução:
x² = 0 + 16
x² = 16
x = √16, portanto, x = ± 4
O conjunto solução será S = {-4, +4}

19. 19
Agora é a sua vez!
(copie e responda no caderno)(copie e responda no caderno)
1) Resolva as equações abaixo:
a) x² - 25 = 0
b) x² - 49 = 0
c) x² - 100 = 0
● d) x² - 3 = 0
● e) x² - 169 = 0

20. 20
f) x² – 1 = 0
g) -144 + x² = 0
h) -x² + 7 = 0
i) x² – 0,36 = 0
2) O quadrado de um número
desconhecido diminuído de 64 unidades é
igual a zero. Calcule esse número.

21. 21
Resolução de equação do 2° grau
incompleta do tipo ax² +bx = 0
● Exemplo: resolver a equação x² – 3x = 0.
uma forma rápida de resolvermos essa equação é
“colocando” o x em evidência.
Assim, teremos: x.(x – 3 ) = 0
x = 0 (que já será uma das raízes)
x – 3 = 0 x = 0 + 3 x = 3 (outra raiz)
● Conclusão:
● O conjunto solução será: S = { 0, 3}
●
●

22. 22
ATENÇÃO!ATENÇÃO!
Toda equação do tipo ax² + bx = 0 terá o 0
(zero) como uma das raízes !!

23. 23
Agora é com vocAgora é com você!
(copie e responda no caderno)
Resolva as equações abaixo:
a) x² + 5x = 0
b) x² - 8x = 0
c) 3x² - 15x = 0
d) 2x² - 8 = 0
e) 3x² = 12x

24. 24
Resolução de equação do 2° grau
completa.
Temos que usar a fórmula de bhaskara.
Δ = b² - 4.a.c e x = -b ± √ Δ
2.a
VOCÊ QUER SABER COMO?VOCÊ QUER SABER COMO?
AGUARDE A PRÓXIMA AULA...AGUARDE A PRÓXIMA AULA...