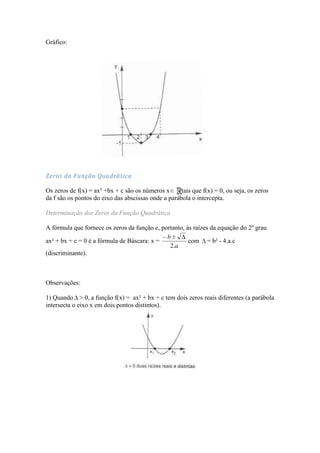
Este documento resume os principais conceitos sobre funções quadráticas, incluindo: (1) a definição de função quadrática como f(x)=ax2+bx+c; (2) que o gráfico de uma função quadrática é uma parábola; (3) que os zeros da função quadrática são os pontos onde a parábola intercepta o eixo x.

1. Apoio Escolar – Explicações – Ana Tapadinhas
Matemática 10º Ano
Função Quadrática
Definição de Função Quadrática
Uma função f: chama-se quadrática quando existem números reais a, b, c, com
a 0, tal que f(x) = ax² + bx + c para todo x .
f:
x  ax² + bx + c
Alguns exemplos:
* f(x) = -x² + 100x, em que a = -1, b = 100 e c = 0
* f(x) = 3x² - 2x + 1, em que a = 3, b = -2 e c = 1
* f(x) = x² - 4, em que a = 1, b = 0 e c = -4
* f(x) = 17x², em que a = 17, b = 0 e c = 0
Observe que não são funções quadráticas:
* f(x) = 3x
* f(x) = 2 x
* f(x) = x³ + 2x² + x + 1
Gráfico da Função Quadrática
O gráfico de uma função quadrática é uma parábola.
Exemplo: f(x) = x² - 4x + 3
Observe a tabela abaixo:
x Y = f(x) = x² -4x + 3 (x, y)
0 3 (0, 3)
1 0 (1, 0)
2 -1 (2, -1)
3 0 (3, 0)
4 3 (4, 3)

2. Gráfico:
Zeros da Função Quadrática
Os zeros de f(x) = ax² +bx + c são os números x tais que f(x) = 0, ou seja, os zeros
da f são os pontos do eixo das abscissas onde a parábola o intercepta.
Determinação dos Zeros da Função Quadrática
A fórmula que fornece os zeros da função e, portanto, às raízes da equação do 2º grau
b
ax² + bx + c = 0 é a fórmula de Báscara: x = com = b² - 4.a.c
2.a
(discriminante).
Observações:
1) Quando > 0, a função f(x) = ax² + bx + c tem dois zeros reais diferentes (a parábola
intersecta o eixo x em dois pontos distintos).

3. 2) Quando = 0, a função f(x) = ax² + bx + c tem um zero real duplo (a parábola
intersecta o eixo x em um só ponto).
3) Quando < 0, a função f(x) = ax² + bx + c não tem zeros reais (a parábola não
intersecta o eixo x).
4) Relação entre coeficientes e raízes da equação ax² + bx + c = 0, com a 0.
Existindo zeros reais tal que:
b b
x1 = e x2 = , obtemos:
2.a 2.a
b b 2b b
x 1 +x 2 = + = =
2.a 2.a 2.a a
b
Logo, x 1 +x 2 = .
a
b b b² ( ) 2 b² b² 4ac c
x1. x 2 = . = = =
2.a 2.a 4a ² 4a ² a
c
Logo, x 1 .x 2 = .
a

4. Gráfico da função definida por f(x) = ax² + bx + c
Vamos estudar o efeito dos parâmetros a, b e c na parábola que representa a função
quadrática f(x) = ax² + bx + c.
Parâmetro a: Responsável pela concavidade e abertura da parábola.
Além disso, quanto maior o valor absoluto de a, menor será a abertura da parábola
(parábola mais “fechada”), independentemente da concavidade.

5. Parâmetro b:
Um ponto ao percorrer a parábola, da esquerda para a direita, ao cruzar o eixo das
ordenadas poderá estar subindo ou descendo.
Se b = 0 o vértice a parábola cruza o eixo y no vértice V, isto é, o vértice V da parábola
está no eixo das ordenadas.
Parâmetro c: Indica o ponto onde a parábola cruza o eixo y.
A parábola cruza o eixo y no ponto (0, c).
Exemplo: Na função quadrática f(x) = ax² + bx + c da figura abaixo, a < 0, b > 0, c > 0.

6. Imagem da Função Quadrática
A determinação do vértice da parábola ajuda na elaboração do gráfico e permite
determinar a imagem da função, bem como seu valor máximo ou mínimo.
As coordenadas do vértice V(x v , y v ) da função quadrática f(x) = ax² + bx + c podem ser
calculadas de duas maneiras:
1ª Maneira: Utilizando as seguintes fórmulas:
b
xv= e yv =
2a 4a
2ª Maneira:
* Para calcular o x v , obtemos as raízes x 1 e x 2 da equação do 2º grau e calculamos o
ponto médio das mesmas. Assim:
x x2
xv= 1
2
* Substituímos o valor do x v na função quadrática para que possamos obter a
coordenada y v .
Examine os exemplos:
1º) f(x) = 2x² - 8x
x1 x2 0 4
Obtendo as raízes, teremos x 1 = 0 e x 2 = 4. Portanto, x v = = =2
2 2
Substituindo x v = 2 na função, obtemos a ordenada do vértice:
y v = f(x v ) = 2 (x v )² - 8(x v )
y v = f(2) = 2 . 2² - 8 . 2 = -8
* O vértice é o ponto (2, 8).
* A função assume valor mínimo -8 quando x = 2
* Im(f) = {y │y 0}
* Essa função não tem valor máximo.
2º) f(x) = -4x² + 4x + 5

7. Sabemos que o vértice V de uma parábola dada por f(x) = ax² + bx + c, a 0, também
b
pode ser calculado assim: V = (x v , y v ) = , .
2a 4a
Neste caso, temos:
f(x) = -4x + 4x + 5
b 4 1
xv= = =
2a 8 2
(16 80) 96
yv= = =6
4a 16 16
V = (1/2, 6)
* O vértice é o ponto (1/2, 6).
* A função assume valor máximo 6 quando x = 1/2
* Im(f) = {y │y 6}
* Essa função não tem valor mínimo.
De modo geral, dada a função f: tal que f(x) = ax² + bx + c, com a 0, se
V (x v , y v ) é o vértice da parábola correspondente, temos então:
a>0 y v é o valor mínimo de f Im(f) = {y │y yv }
a<0 y v é o valor máximo de f Im(f) = {y │y yv }

8. Estudo do sinal da função quadrática
Estudar o sinal da função quadrática f(x) = ax² + bx + c, a 0, significa determinar os
valores reais de x para os quais f(x) se anula (f(x) = 0), f(x) é positiva (f(x) > 0) e f(x) é
negativa (f(x) < 0).
O estudo do sinal da função quadrática vai depender do discriminante = b² - 4ac da
equação do 2º grau correspondente ax² + bx + c = 0 e do coeficiente a.
Dependendo do discriminante, podem ocorrer três casos e, em cada caso, de acordo com
o coeficiente a, podem ocorrer duas situações. Portanto, temos um total de seis casos.
Acompanhe:
1º Caso: > 0
Neste caso:
* A função admite dois zeros reais distintos, x 1 e x 2 ;
* A parábola que representa a função intersecta o eixo x em dois pontos.
a>0 a<0
f(x) = 0 para x = x 1 ou x = x 2
f(x) = 0 para x = x 1 ou x = x 2
f(x) > 0 para x < x 1 ou x > x 2 f(x) > 0 para x 1 < x < x 2
f(x) < 0 para x 2 < x < x 1 f(x) < 0 para x < x 1 ou x > x 2
2º Caso: =0
Neste caso:
* A função admite um zero real duplo x 1 = x 2
* A parábola que representa a função tangencia o eixo x.
a>0 a<0
f(x) = 0 para x = x 1 = x 2 f(x) = 0 para x = x 1 = x 2
f(x) > 0 para x x 1 f(x) < 0 para x x 1

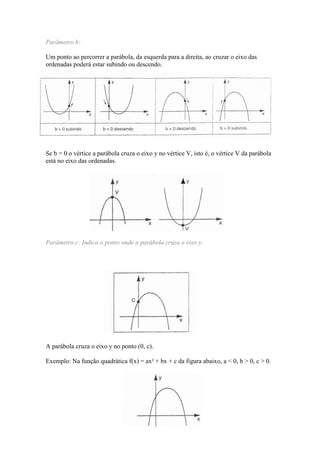
9. 3º Caso: <0
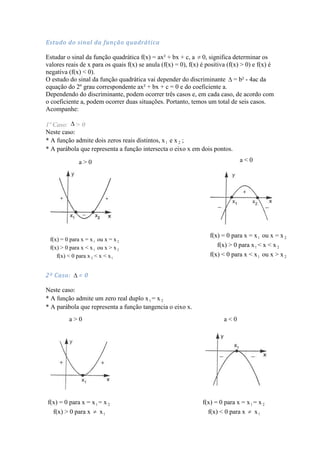
Neste caso:
* A função não admite zeros reais;
* A parábola que representa a função não intersecta o eixo x.
a>0 a<0
f(x) > 0 para todo x real f(x) < 0 para todo x real
Exemplos:
1º) Vamos estudar os sinais das seguintes funções:
a) f(x) = x² - 7x + 6 b) f(x) = 9x² + 6x + 1 c) f(x) = -2x² +3x – 4
a) f(x) = x² - 7x + 6
a=1>0
= (-7)² - 4 (1) (6) = 25 > 0
Zeros da função: x 1 = 6 e x 2 = 1
Então:
* f(x) = 0 para x = 1 ou x = 6
* f(x)< 0 para x < 1 ou x > 6
* f(x) < 0 para 1 < x < 6
Portanto, f(x) é positiva para x fora do intervalo [1, 6], é nula para x = 1 ou x = 6 e
negativa para x entre 1 e 6.
b) f(x) = 9x² + 6x + 1
a=9>0
= (6)² - 4 (9) (1) = 0
Zeros da função: x = -1/3

10. Então:
* f(x) = 0 para x = -1/3
* f(x) > 0 para todo x -1/3
c) f(x) = -2x² +3x – 4
a = -2 < 0
= (3)² - 4 (-2) (-4) = -23 < 0
Portanto, < 0 e a função não tem zeros reais.
Logo, f(x) < 0 para todo x real, ou seja, f(x) é sempre negativa.
2º) Quais são os valores reais de k para que a função f(x) = x² - 2x + k seja positiva para
todo x real?
Condições:
* a > 0 (já satisfeita, pois a = 1 > 0)
* <0
Cálculo de :
= (-2)² - 4 (1) (k) = 4 – 4k
Daí:
4 – 4k < 0 -4k < -4 4k > 4 k >4/4 k>1
Logo, k │k > 1.