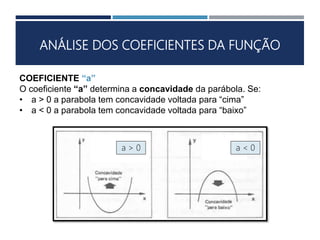
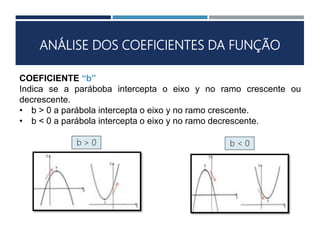
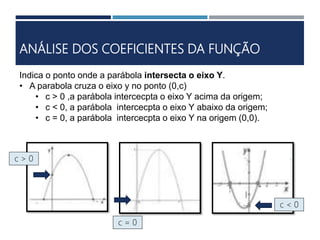
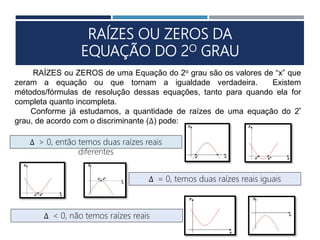
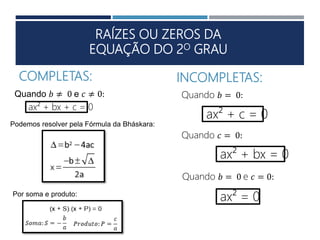
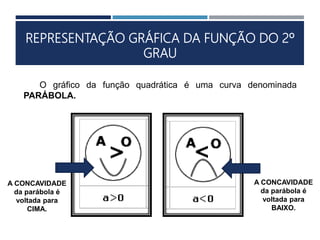
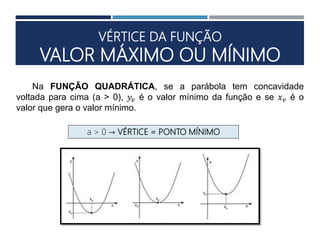
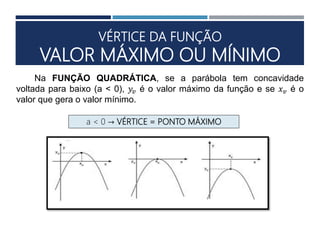
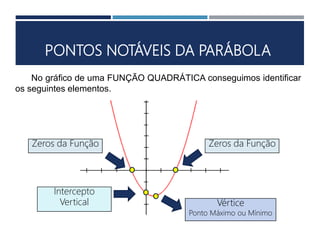
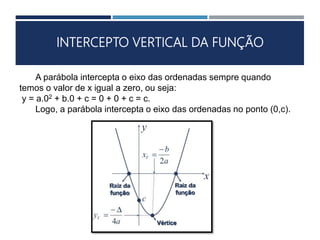
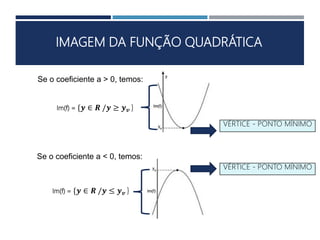
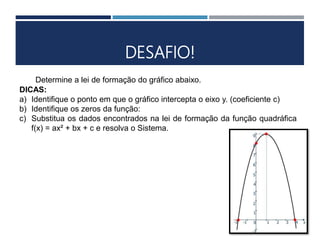
Este documento apresenta os conceitos fundamentais sobre funções polinomiais do 2o grau. Inicia definindo a função do tipo f(x) = ax2 + bx + c e exemplificando a determinação dos coeficientes a, b e c. Em seguida, analisa cada um dos coeficientes e sua relação com a forma da parábola. Por fim, aborda tópicos como cálculo numérico da função, raízes, representação gráfica e elementos notáveis da parábola.

1. PROFESSORA: FABÍOLA

2. FUNÇÃO DO 2° GRAU
Uma função polinomial do 2º grau é uma função do tipo
y = ax² + bx + c ou f(x) = ax² + bx + c, com a, b e c números
reais e a ≠ 0.
EXEMPLOS:
1- Determine os coeficientes a, b e c nas funções abaixo:
y = 3x² + 2x + 1
y = x² - 5x + 2
y = 4x - x² + 6
y = 3 x + x²
y = x² - 4
y = -2x²

3. EXEMPLOS:
Nem sempre nossa expressão algébrica aparecerá na forma
y = ax² + bx + c, mas através de manipulações algébricas
conseguimos identificar os coeficientes:
a) f(x) = (x + 2)² b) f(x) = 3x.(x – 1)

4. ANÁLISE DOS COEFICIENTES DA FUNÇÃO
COEFICIENTE “a”
O coeficiente “a” determina a concavidade da parábola. Se:
• a > 0 a parabola tem concavidade voltada para “cima”
• a < 0 a parabola tem concavidade voltada para “baixo”
a > 0 a < 0

5. ANÁLISE DOS COEFICIENTES DA FUNÇÃO
COEFICIENTE “b”
Indica se a paráboba intercepta o eixo y no ramo crescente ou
decrescente.
• b > 0 a parábola intercepta o eixo y no ramo crescente.
• b < 0 a parábola intercepta o eixo y no ramo decrescente.
b > 0 b < 0

6. ANÁLISE DOS COEFICIENTES DA FUNÇÃO
Indica o ponto onde a parábola intersecta o eixo Y.
• A parabola cruza o eixo y no ponto (0,c)
• c > 0 ,a parábola intercecpta o eixo Y acima da origem;
• c < 0, a parábola intercecpta o eixo Y abaixo da origem;
• c = 0, a parábola intercecpta o eixo Y na origem (0,0).
c > 0
c = 0
c < 0

7. VALOR NUMÉRICO DA FUNÇÃO DO 2° GRAU
A forma geral desse tipo de função pode ser dada por
f(x) = ax² + bx + c. Dado o valor de x, o cálculo de y ou f(x) é realizado
por meio de substituição desses valores na função dada.
Exemplos:
 Dada a função f(x) = x² – 3x + 2, determinar o valor de:
a) f(–1) b) f(3).

8. EXEMPLOS:
 Dada a função f(x) = 3x² – x + 2, determinar o valor de:
a) f(–1) b) f(0). c) f(
1
2
).

9. EXEMPLO:
O resultado da expressão 2x² - 3x + 10, para x= -2, é:
 a) 12
 b) – 4
 c) 24
 d) 8

10. EXEMPLO:
Um copo lançado do solo verticalmente para cima tem posição
em função do tempo dada pela função h(t) = 40t – 5t², em que a
altura h é dada em metros e o tempo t é dado em segundos.
Determine a altura em que o corpo se encontra em relação ao solo
no instante de t = 3s.
a) 45 m
b) 105 m
c) 75 m
d) 115 m

11. EXEMPLO:
As funções do 2º grau têm diversas aplicações no nosso
cotidiano. Por exemplo: Considere que numa padaria na cidade de
São Paulo, a receita diária R(x) (em reais) depende da quantidade
“x” vendida e é obtida através da função descrita a seguir:
R(x) = x² – 10x
Com base nessas informações, a receita diária obtida com a
venda de 20 pães é igual a:
a) R$ 200,00
b) R$ 150,00
c) R$ 100,00
d) R$ 50,00

12. RAÍZES OU ZEROS DA
EQUAÇÃO DO 2O GRAU
RAÍZES ou ZEROS de uma Equação do 2o grau são os valores de “x” que
zeram a equação ou que tornam a igualdade verdadeira. Existem
métodos/fórmulas de resolução dessas equações, tanto para quando ela for
completa quanto incompleta.
Conforme já estudamos, a quantidade de raízes de uma equação do 2º
grau, de acordo com o discriminante (∆) pode:
∆ > 0, então temos duas raízes reais
diferentes
∆ = 0, temos duas raízes reais iguais
∆ < 0, não temos raízes reais

13. RAÍZES OU ZEROS DA
EQUAÇÃO DO 2O GRAU
ax² + bx + c = 0
COMPLETAS: INCOMPLETAS:
Quando 𝑏 ≠ 0 e 𝑐 ≠ 0:
Quando 𝑏 = 0 e 𝑐 = 0:
Quando 𝑏 = 0:
Quando 𝑐 = 0:
ax² + c = 0
ax² + bx = 0
ax² = 0
Podemos resolver pela Fórmula da Bháskara:
Por soma e produto:

14. EXEMPLOS:
Calcule as raízes da equação das seguintes funções:
a) f(x) = x² - 4 b) f(x) = x² - 3x
c) f(x) = 3x² d) f(x) = x(x + 3) − 5x

15. EXEMPLOS:
Calcule as raízes da equação da seguinte função:
a) f(x) = x² + 9x + 18

16. EXEMPLOS:
Calcule as raízes da equação da seguinte função:
b) f(x) = x² – 2x – 1

17. EXEMPLOS:
Calcule as raízes da equação da seguinte função:
b) f(x) = x² – 3x + 9

18. REPRESENTAÇÃO GRÁFICA DA FUNÇÃO DO 2º
GRAU
O gráfico da função quadrática é uma curva denominada
PARÁBOLA.
A CONCAVIDADE
da parábola é
voltada para
CIMA.
A CONCAVIDADE
da parábola é
voltada para
BAIXO.

19. REPRESENTAÇÃO GRÁFICA DA FUNÇÃO DO 2º
GRAU
Observe a função quadrática e responda se o gráfico da parábola
tem concavidade voltada para cima ou para baixo:
a) f(x) = x² - 4x + 3
b) f(x) = -x² + 3x – 2
c) f(x) = 2x² - 8x + 8
d) f(x) = x² - 4
e) f(x) = -x² - 3x
f) f(x) = -3x² + 6x - 5

20. GRÁFICO DA FUNÇÃO DO 2° GRAU
Seja a função definida por:
f(x) = x² - 4x + 3
Complete a tabela e construa o gráfico da função:
x f(x) = x² - 4x + 3 f(x) (x,f(x))
0
1
2
3
4

21. GRÁFICO DA FUNÇÃO DO 2° GRAU
Seja a função definida por:
f(x) = -x² + 6x - 8
Complete a tabela e construa o gráfico da função:
x f(x) = -x² + 6x - 8 f(x) (x,f(x))
1
2
3
4
5

22. VÉRTICE DA FUNÇÃO
VALOR MÁXIMO OU MÍNIMO
Na FUNÇÃO QUADRÁTICA, se a parábola tem concavidade
voltada para cima (a > 0), 𝑦𝑣 é o valor mínimo da função e se 𝑥𝑣 é o
valor que gera o valor mínimo.
a > 0 → VÉRTICE = PONTO MÍNIMO

23. VÉRTICE DA FUNÇÃO
VALOR MÁXIMO OU MÍNIMO
Na FUNÇÃO QUADRÁTICA, se a parábola tem concavidade
voltada para baixo (a < 0), 𝑦𝑣 é o valor máximo da função e se 𝑥𝑣 é o
valor que gera o valor mínimo.
a < 0 → VÉRTICE = PONTO MÁXIMO

24. VÉRTICE DA FUNÇÃO QUADRÁTICA
 Se a > 0, o vértice é o ponto MÍNIMO da função;
 Se a < 0, o vértice é o ponto MÁXIMO da função;
 Calculamos o vértice da função ( V(x.y) ) da seguinte forma:

25. EXEMPLO:
 Determinar o vértice da função do 2° grau f(x) = x² - 4x + 3
DICA:

26. EXEMPLO:
 Determinar o vértice da função do 2° grau f(x) = -x² - 6x + 9
DICA:

27. EXEMPLO:
Um carrinho se move sobre um arco de parábola de uma
montanha-russa, de modo que sua altura em relação ao solo, em
metros, é dada em função do tempo “t”, medido em segundos, pela
equação
h(t) = 2t² – 8t + 11.
Então, o menor valor de “h” é igual a:
a) 2 m.
b) 3 m.
c) 4 m.
d) 5 m.

28. EXEMPLO:
Uma bola lançada para cima, verticalmente, tem sua altura “h”
(em metros) dada em função do tempo “t” (em segundos) decorrido
após o lançamento pela fórmula h = – 5t² + 20t. Então a altura
máxima atingida pela bola é:
a) 5 m.
b) 25 m.
c) 15 m.
d) 10 m.
e) 20 m.

29. EXEMPLO:
O custo diário de produção de uma indústria de computadores é
dado pela função C(x) = x² – 92x + 2800, onde C(x) é o custo em
reais, e “x” é o número de unidades fabricadas. Quantos
computadores devem ser produzidos diariamente para que o custo
seja mínimo?
a) 128
b) 2800
c) 46
d) 92
e) 684

30. PONTOS NOTÁVEIS DA PARÁBOLA
No gráfico de uma FUNÇÃO QUADRÁTICA conseguimos identificar
os seguintes elementos.
Zeros da Função
Vértice
Ponto Máximo ou Mínimo
Intercepto
Vertical
Zeros da Função

31. INTERCEPTO VERTICAL DA FUNÇÃO
A parábola intercepta o eixo das ordenadas sempre quando
temos o valor de x igual a zero, ou seja:
y = a.02 + b.0 + c = 0 + 0 + c = c.
Logo, a parábola intercepta o eixo das ordenadas no ponto (0,c).

32. EXEMPLOS
Seja a função definida por f(x) = x² - 4x + 3, construa o gráfico da
função com os seguintes dados:
a) Ponto que intercepta o eixo x
b) Zeros da função
c) Vértice da parábola

33. EXEMPLOS
Seja a função definida por f(x) = -x² + 5x - 6, construa o gráfico da
função com os seguintes dados:
a) Ponto que intercepta o eixo x
b) Zeros da função
c) Vértice da parábola

34. IMAGEM DA FUNÇÃO QUADRÁTICA
VÉRTICE - PONTO MÍNIMO
Se o coeficiente a > 0, temos:
Im(f) = {𝒚 ∈ 𝑹 /𝒚 ≥ 𝒚𝒗 }
Im(f) = {𝒚 ∈ 𝑹 /𝒚 ≤ 𝒚𝒗 }
Se o coeficiente a < 0, temos:
VÉRTICE - PONTO MÍNIMO

35. DESAFIO!
Determine a lei de formação do gráfico abaixo.
DICAS:
a) Identifique o ponto em que o gráfico intercepta o eixo y. (coeficiente c)
b) Identifique os zeros da função:
c) Substitua os dados encontrados na lei de formação da função quadráfica
f(x) = ax² + bx + c e resolva o Sistema.

36. AGORA É A SUA VEZ
DE PRATICAR!
FAÇA OS EXERCÍCIOS PROPOSTOS COM ATENÇÃO!