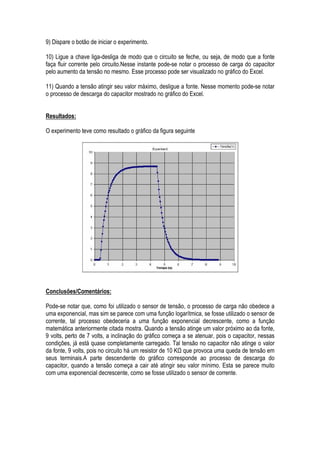
O documento apresenta uma introdução sobre funções exponenciais e seu uso em diversas áreas como física, química e biologia. Em seguida, exemplifica o cálculo do número de antepassados de um casal usando funções exponenciais e apresenta a definição formal de função exponencial e algumas de suas propriedades gráficas e algébricas.

1. FUNÇÕES EXPONENCIAIS
Introdução:
A função exponencial é uma das mais importantes para a explicação e estudos de muitos
fenômenos naturais e também para o projeto de muitas máquinas, é ferramenta indispensável
para físicos, químicos, biólogos e também para engenheiros, que devem sabê-la muito bem para
aplicá-la em seus trabalhos tanto na pesquisas, caso dos físicos, químicos e biólogos, como
também na engenharia, caso dos engenheiros.
Para exemplificar como a função exponencial está presente no dia-a-dia dos estudos dos
cientistas, vamos analisar um pequeno exemplo de árvore genealógica. Gustavo e Karina
formam um casal que em suas famílias as pessoas vivem muito tempo. Vamos calcular quantos
avós e bisavós têm em conjunto Gustavo e Karina. para iniciarmos contamos quantos os pais de
cada um e depois somamos, depois os avós e por último os bisavós. Assim temos:
pais → 2 + 2 = 4 = 22
avôs/avós → 4 + 4 = 8 = 23
bisavôs/bisavós → 8 + 8 = 16 = 24
Observamos assim que a cada passo o número de pessoas dobra. Se continuássemos
calculando o número de pessoas na quinta geração (trisavôs / trisavós), teríamos:
16 + 16 = 32 = 25
Notamos assim que para cada geração x que se escolha há um número f(x) de ascendentes em
função de x, e a lei que expressa f(x) em função de x é f(x) = 2x, que é um caso particular de
função exponencial.
Esse pequeno exemplo expressa o número de pais, avôs e avós, bisavôs e bisavós, etc... de
Gustavo e Karina. No estudo de muitos casos que envolva as gerações de populações animais,
por exemplo, os biólogos fazem uso da função exponencial para estudar o comportamento de
tais populações, por exemplo o crescimento de uma cultura de peixes numa lagoa, a evolução
de uma população de bactérias em certo organismo, o estudo do Caos de uma população animal
é um excelente exemplo de estudo utilizando a função exponencial.
DEFINIÇÃO DA FUNÇÃO EXPONENCIAL:
Uma função exponencial qualquer função f de R em R dada pela lei da forma f(x) = ax, onde a é
um número real e, a > 0 e a ≠ 1. A é chamado de base da função.
GRÁFICO:
Os gráficos da função exponencial podem ser crescentes ou decrescentes, dependendo do valor
de a ou do sinal do expoente. Vejamos alguns casos:

2. a>1 a < 1, ou expoente negativo
PROPRIEDADES:
Vamos analisar algumas propriedades do gráfico da função exponencial f(x) = ax
1) se x = 0 → f(x) = 1, pois a0 = 1, todo número elevado a zero resulta em 1. Isso quer dizer que
o gráfico de qualquer função exponencial do tipo f(x) = ax corta o eixo das ordenadas no ponto
de ordenada igual a 1, par (01).
2) Se a > 1, então a função f(x) = ax é crescente.
3) Se 0 < a < 1, então a função f(x) = ax é decrescente. São decrescentes por exemplo as
funções exponenciais:
x x x
1 2  3
f (x ) =   , f (x ) =   , f (x ) =  
4 3 5
4) Para todo a > 0 e todo x real, temos ax > 0; portanto, o gráfico da função f(x) = ax está sempre
acima do eixo das abscissas.
Se a > 1, então ax aproxima-se de zero quando x assume valores negativos cada vez menores.
Se 0 < a < 1, então ax aproxima-se de zero quando x assume calores positivos cada vez
maiores.
5) Se tivermos no expoente o sinal de menos, f(x) = a-x, o gráfico da função será decrescente
também.
EQUAÇÕES EXPONENCIAIS:
Equações exponenciais são as equações que apresentam a incógnita no expoente de pelo
menos uma potência. São exemplos de equações exponenciais:
x
1
2 = 16 ,   = 81 , 4 x − 2 x = 12
x
8
Um método muito utilizado para se resolver equações exponenciais consiste em reduzir ambos
os membros da equação a potência de mesma base a (0< a ≠ 1), e depois aplicar a propriedade:

3. a x1 = a x2 ⇒ x1 = x 2
Quando isso é possível, a equação exponencial é facilmente resolvida.
INEQUAÇÕES EXPONENCIAIS:
Inequações exponenciais são as equações que apresentam a incógnita no expoente de pelo
menos uma potência. São exemplos de equações exponenciais:
x
1
2 > 16 ,   < 27 , 4 x − 2 x ≤ 12
x
3
Um método muito utilizado para se resolver equações exponenciais consiste em reduzir ambos
os membros da equação a potência de mesma base a (0< a ≠ 1), e depois aplicar a propriedade:
a x1 < a x2 ⇒ x1 < x 2 , (se a > 1)
a x1 < a x2 ⇒ x1 > x 2 , (se 0 < a < 1)
Experiência de Matemática
Material utilizado:
• Sensor de tensão KDS-1009 da VOLTCOM,
• Capacitor eletrolítico de 470 µF e 50 v,
• Resistor de 10 K (10000 ohms),
• Chave liga-desliga,
• Matriz de contatos Prot-on-Board
• Fonte de tensão de 50 v.
Procedimento experimental:
Para o experimento hora proposto devemos seguir os seguintes passos.
1) Conecte o a interface com o PC pela porta USB.
2) Conecte o sensor de movimento à interface.
3) Ligue o PC e a interface.
4) Ligue o capacitor na matriz de contatos.
5) Ligue o resistor em série com o capacitor na matriz de contatos.
6) Ligue a chave liga-desliga em série com o capacitor e com o resistor deixando-a na posição
de modo que o circuito fique aberto.
7) Ligue a fonte de tensão nos terminais do circuito montado.
8) Ligue o sensor de tensão em paralelo com o capacitor.

4. 9) Dispare o botão de iniciar o experimento.
10) Ligue a chave liga-desliga de modo que o circuito se feche, ou seja, de modo que a fonte
faça fluir corrente pelo circuito.Nesse instante pode-se notar o processo de carga do capacitor
pelo aumento da tensão no mesmo. Esse processo pode ser visualizado no gráfico do Excel.
11) Quando a tensão atingir seu valor máximo, desligue a fonte. Nesse momento pode-se notar
o processo de descarga do capacitor mostrado no gráfico do Excel.
Resultados:
O experimento teve como resultado o gráfico da figura seguinte
Conclusões/Comentários:
Pode-se notar que, como foi utilizado o sensor de tensão, o processo de carga não obedece a
uma exponencial, mas sim se parece com uma função logarítmica, se fosse utilizado o sensor de
corrente, tal processo obedeceria a uma função exponencial decrescente, como a função
matemática anteriormente citada mostra. Quando a tensão atinge um valor próximo ao da fonte,
9 volts, perto de 7 volts, a inclinação do gráfico começa a se atenuar, pois o capacitor, nessas
condições, já está quase completamente carregado. Tal tensão no capacitor não atinge o valor
da fonte, 9 volts, pois no circuito há um resistor de 10 K que provoca uma queda de tensão em
seus terminais.A parte descendente do gráfico corresponde ao processo de descarga do
capacitor, quando a tensão começa a cair até atingir seu valor mínimo. Esta se parece muito
com uma exponencial decrescente, como se fosse utilizado o sensor de corrente.

5. Exercícios Resolvidos
1) Construa o gráfico da seguinte função exponencial: f (x ) = 2 x
x
1
2) Construa o gráfico da seguinte função exponencial: f (x ) =  
2
3) Resolver as seguintes equações exponenciais:
a-) 2 x = 16
x
1
b-)   = 81
3
c-) ( 2) x
= 64
4) Resolver as seguintes equações exponenciais:
a-) (3 )
x x +1
= 729
b-) 2 2 x +1 ∗ 4 3 x +1 = 8 x −1
5) Resolva a equação exponencial 4 x − 2 x = 12
6) Resolver a seguinte equação exponencial: 9 x+1 − 4 ∗ 3 x − 69 = 0
7) Para exemplificar a resolução de uma inequação exponencial vamos resolver as seguintes
inequações:
a-) 2 x > 64
x
1
b-)   ≤ 27
3
c-) ( 2) x
≥4 2
d-) (0,56)2 x +3 > 1
8) Resolver as seguintes inequações exponenciais:

6. a-) (2 )x x +1
≤ 64
3 x +1 x −1
 1  1+ 2 x − x 2  1 
b-)  x  ∗9 ≥ 
3   27 
9) Resolver a equação exponencial 5 2 x +1 − 5 x +3 > 5 x − 5
10) Resolver a equação exponencial 7 x − 6 ≥ 71− x
Exercícios Propostos:
1) Construa os gráficos das seguintes funções exponenciais:
x
1
a-) f ( x ) =  
3
b-) f (x ) = 2 − x
x +1
c-) f (x ) = 3 2
d-) f ( x ) = 21− x
2) Para que valores de m a função f ( x ) = 2 ∗ m é crescente ?
x
f ( x ) = 4 ∗ (m − 2) é crescente. Determine m.
x
3) A função
f ( x ) = 0,1 ∗ (m − 1)
x
4) Determine m para que a função seja crescente.
5) Resolva as seguintes equações exponenciais:
x
1
a-)   = 125
5
b-) ( 3)
4
x
=3 9

7. c-) 8 2 x +1 = 3 4 x −1
1 7 x −1
d-) = 49
7
6) Resolva as seguintes equações exponenciais:
a-) 2 x +1 − 2 3− x = 6
8
b-) 2 x +3 + 63 =
2x
7) Resolva as seguintes inequações exponenciais:
a-) ( 3 )
x 1
3
≤
9
b-) ( 2 )
x 1
> 3
16
c-) 4x ≥ 8
9.8) Resolva as seguintes inequações exponenciais:
a-) (27 )x − 2 x +1
( )
≥ 9 x +1
x −3
3 x−2 2 x +1 x −3
2 4  8 
b-)   ∗  ≤ 
3 9  27 
− 2 x +1 5625
=
2
x
9) Qual a soma das raízes da equação: 5
9
(0,8)4 x − x > (0,8)3( x+1)
2
10) Quais os valores de x que tornam válida a desigualdade: