Função exponencial logaritmo_2012

Professor Cristiano Marcell

Colégio Pedro II Propriedades da função exponencial
Unidade Realengo II - 2012
Lista de Função Exponencial e Logarítmica.  O domínio da função exponencial é R, isto é, d(f) = R
Prof. Cristiano Marcell  A imagem da função exponencial é R+*, isto é, Im(f) = R+*
 Em qualquer caso, o gráfico corta o eixo y no ponto P(0, 1)
 Se a > 1, a função é crescente, pois x1 > x2 ⤇ ax1 > ax2
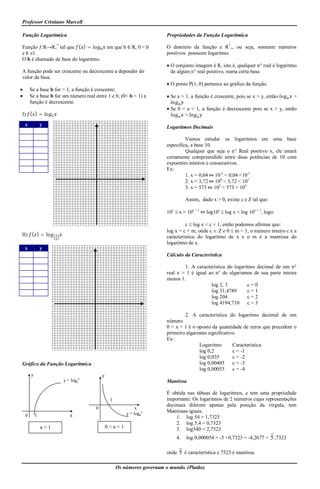
Função Exponencial
 Se 0 < a < 1, a função é decrescente, pois x1 > x2 ⤇ ax1< ax2
Função ƒ:R→R+* tal que ƒ(x)= ax em que a ∈ R, 0 < a e a≠1.
Equações exponenciais
O a é chamado de base e o x de expoente.
Apresentam variáveis em expoente.Vamos resolver algumas:
A função pode ser crescente ou decrescente a depender do
valor da base.

 Se a base a for > 1, a função é crescente;
 Se a base a for um número real entre 1 e 0, (0< a < 1) a
função é decrescente.

I) f(x) = 2x

x y

Inequações exponenciais

São inequações que apresentam variável em expoente.

I) 2x < 2
II) 3x-1  9

Resolução de equações exponenciais

Se b e c são números reais, então:
II) ( ) =
 a > 1 ⤇ ab > ac ⤇ b > c
x y  0 < a < 1 ⤇ ab > ac ⤇ b < c

Exercícios

Questão 1) Considere a função de IR em IR dada por f(x)=5x
+3. Seu conjunto-imagem é
a) ]- ∞; 3[ b) ]- ∞; 5[ c) [3; 5] d) ]3; +∞[

Questão 2) O número real que é raiz da equação

5 x+2 + 5 x-1 +5 x+1+ 5 x = 78 é:

a) 1 b) 2 c) 3 d) 4

Questão 3) Os pontos A = (1, 6) e B = (2,18) pertencem ao
gráfico da função y = nax. Então, o valor de an é:

a) 6 b) 9 c) 12 d) 16

Gráfico da função exponencial Questão 4) Uma das soluções da equação
y é:
y
a) x = 1
b) x = 0
1 c) x = -2
1 d) x = 3
0 x Questão 5) Na equação 2x+1 + 2-x = 3, é verdadeira a
0 x
a>1 0<a<1 afirmativa:

Os números governam o mundo. (Platão)

a) Uma das raízes é 1.
b) A soma das raízes é um número inteiro positivo. Questão 15) Se x e y são números reais que tornam
c) O produto das raízes é um número inteiro negativo. simultaneamente verdadeiras as sentenças 2x+y-2 = 30 e 2x - y-
d) O quociente das raízes pode ser zero (0). 2 = 0, então xy é igual a:
2
x
Questão 6) Os valores de x para os quais (0,8) 4 x 
a) 9 b) 8 c)1/8 d) 1/9
3( x  1)
(0,8) são
3 1 3 1 Questão 16) Ao estudar o processo de reprodução em uma
a)   x  c) x   ou x  cultura de bactérias, um grupo de biólogos, a partir de dados
2 2 2 2 experimentais coletados em um determinado período de
1 3 1 3 tempo, concluiu que o número aproximado de indivíduos, N,
b)   x  d) x   ou x  em função do tempo t em horas, é dado por N(t) = 50.20,3t .
2 2 2 2
Dessa forma, a cultura terá 3200 indivíduos depois de

a) 12 horas.
Questão 7) O conjunto-solução da inequação (0,5) x(x - 2)
< b) 20 horas.
(0,25)x - 1,5 é c) 15 horas.
d) 23 horas.
a) {x  R / x <1}. b) {x  R / x >3}. e) 18 horas.
c) {x  R / 1 < x <3}. d) {x R / x < 1 ou x > 3}
Questão 17) Resolva 3x-1 - 3x + 3x+1 + 3x+2 = 306
Questão 8) Dentre as identidades a seguir, marque a FALSA.
Questão 18) A produção de uma indústria vem diminuindo
2 ano a ano. Num certo ano, ela produziu mil unidades de seu
 4 1 6 2 
a)     0,81 principal produto. A partir daí, a produção anual passou a
 2 2 2 2 
  seguir a lei
38 . 44 27 y = 1000.(0,9)x. O número de unidades produzidas no
b)  segundo ano desse período recessivo foi de:
6 . 124 2

c)   2 2  3  27 a) 900 b) 1000 c) 180 d) 810 e) 90
1
 3  50  2
6
Questão 19) Num período prolongado de seca, a variação da
1728 quantidade de água de certo reservatório é dada pela função
d)  3
6
64 q(t) = q0 . 2(-0,1)t
sendo q0 quantidade inicial de água no reservatório e
Questão 9) Se 3x + 3-x = 5 então 2.(9x +9-x) é igual a q(t) a quantidade de água no reservatório após t meses. Em
quantos meses a quantidade de água do reservatório se
a) 50 b)25 c) 46 d)23 reduzirá à metade do que era no início?

Questão 10) No intervalo [–1, 100], o número de soluções a) 5. b) 7. c) 8. d) 9. e) 10.
inteiras da inequação 3x – 8 > 32–x é
Questão 20) Cássia aplicou o capital de R$ 15.000,00 a juros
a) 97 b)98 c)99 d)100 compostos, pelo período de 10 meses e à taxa de 2% a.m. (ao
mês). Considerando a aproximação (1,02)5 = 1,1, Cássia
Questão 11) O produto das soluções da equação 2x – 2-x = 5 computou o valor aproximado do montante a ser recebido ao
(1 – 2-x) é final da aplicação. Esse valor é:

a) 0 b) 2 c) 1 d) 4 a) R$ 18.750,00. b) R$ 18.150,00. c) R$ 17.250,00.
d) R$ 17.150,00. e) R$ 16.500,00.
Questão 12) Num laboratório é realizada uma experiência
com um material volátil, cuja velocidade de volatização é Questão 21) Certa substância radioativa desintegra-se de
medida pela sua massa, em gramas, que decresce em função modo que, decorrido o tempo t, em anos, a quantidade ainda
do tempo t, em horas, de acordo com a fórmula não desintegrada da substância é

m = -32t – 3t +1 + 108. S = S0.2-0,25t
Assim sendo, o tempo máximo de que os cientistas dispõem
para utilizar este material antes que ele volatilize totalmente em que S0 representa a quantidade de substância que havia no
é: início. Qual é o valor de t para que a metade da quantidade
inicial desintegre-se?
a) superior a 15 minutos e inferior a 30 minutos
b) superior a 30 minutos e inferior a 60 minutos Questão 22) Uma população de bactérias começa com 100 e
c) superior a 60 minutos e inferior a 90 minutos dobra a cada três horas. Assim, o número n de bactérias após
d) superior a 90 minutos e inferior a 120 minutos t horas é dado pela função N(t) = 100.2t/3
Nessas condições, pode-se afirmar que a população será de
Questão 13) Se 8x-9 =16x/2, então x é um número múltiplo de: 51.200 bactérias depois de:
a) 1 dia e 3 horas.
a) 2 b) 3 c) 5 d) 7 b) 1 dia e 9 horas.
c) 1 dia e 14 horas.
Questão 14) Se (0,0625)x+2 = 0,25, então (x+1)6 vale: d) 1 dia e 19 horas.

a) -3/2 b) 1/32 c) 64 d) 1/64



Questão 23) No programa de rádio HORA NACIONAL, o Conseqüências da definição
locutor informa:
 log b1 = 0
"Atenção, senhores ouvintes. Acabamos de receber uma  log b b = 1
notificação da defesa civil do País alertando para a chegada  logb bn = n
de um furacão de grandes proporções nas próximas 24 log b a
horas. Pede-se que mantenham a calma, uma vez que os  b =a
órgãos do governo já estão tomando todas as providências
cabíveis". Propriedades

Para atender às solicitações que seguem, suponha que o  log a (b . c) = log ab + loga c
número de pessoas que tenha acesso a essa informação,
a
quando transcorridas t horas após a divulgação da notícia,  log a = log ab - loga c
seja dado pela expressão b
 log a an = n. loga n

 = , onde c > 0 e c  1
( )=
1 + 9. 2 Logaritmo de uma Raiz

Se 0 < a  1, b > 0 e n  N*, então:
sendo t ≥ 0 e P a população do País.
1
a) Calcule o percentual da população que tomou n
b bn 1
 log a  log a  log b
a
conhecimento da notícia no instante de sua divulgação. n
b) Calcule em quantas horas 90% da população tem acesso à Concluímos que = .
notícia, considerando que, em 1 hora após a notícia, 50% da
população do país já conhecia a informação.
Equações logarítmicas
Questão 24) A equação 2x = - 3x + 2, com x real,
a) não tem solução. Apresentam variável em logaritmo, no logaritmo ou base.
b) tem uma única solução entre 0 e 2/3.
c) tem uma única solução entre - 2/3 e 0. a) log(x – 1)2 = 3 c) log (x + 1) x – 1 = 2
d) tem duas soluções, sendo uma positiva b) log 2x = 31 d) log xx2 - 1 = 1
e outra negativa.
e) tem mais de duas soluções. Ao resolvermos uma equação logarítmica, devemos
observar as restrições a que devemos estar submetidos os
Questão 25) Qualquer quantidade de massa do chumbo 210 logaritmandos, as bases, e conseqüentemente a incógnita, são
diminui em função do tempo devido à desintegração elas:
radioativa. Essa variação pode ser descrita pela função  O logaritmando deve ser positivo
exponencial dada por m=m0.2-xt . Nessa sentença, mx é a  A base deve ser positiva e diferente de 1
massa (em gramas) no tempo t (em anos), m0 é a massa 
inicial e x é uma constante real.
Sabendo-se que, após 66 anos, tem-se apenas 1/8 da massa Inequações Logarítmicas
inicial, o valor x é:
Envolvem variável em logaritmo ou na base, ou no logaritmo.
a) – 3 b) 1/3 c) – 22 d) 1/22 e) 1/8 Para resolvermos uma inequação logarítmica, devemos estar
atentos, às restrições a que devem estar submetidas as
incógnitas vamos estudar os tipos possíveis:
Função Logarítimica
1.° Tipo: log f(x)a > log g(x)a, 0< a  1
A palavra logaritmo vem do grego: logos= razão e arithmos=
número. Se a > 1, então f(x) > g (x) > 0
Se 0 < a 1, então 0< f(x) , g(x)
logba = c  bx = c
2.° Tipo: log f(x)a > k; 0 < a  1, k  R
Chamamos a de antilogaritmo; b, de base (maior que zero e
diferente de 1) e c de logaritmo.

Se a > 1, então: f(x) > ak

Se 0 < a < 1, então: 0 < f(x) < ak
Calcular o logaritmo de a na base b é o mesmo que encontrar
um expoente que colocado em b, resulte numa potência igual 3.° Tipo: Incógnita Auxiliar:
a a. São as inequações que resolvemos fazendo uma mudança de
incógnitas.
Condição de existência

 a>0
 b>0eb1



Função Logarítmica Propriedades da Função Logarítmica

Função ƒ:R→R+* tal que ( ) = em que b ∈ R, 0 < b O domínio da função e R*+, ou seja, somente números
e b ≠1. positivos possuem logaritmo.
O b é chamado de base do logaritmo.
 O conjunto imagem é R, isto é, qualquer n° real é logaritmo
A função pode ser crescente ou decrescente a depender do de algum n° real positivo, numa certa base.
valor da base.
 O ponto P(1, 0) pertence ao gráfico da função.
 Se a base b for > 1, a função é crescente;
 Se a base b for um número real entre 1 e 0, (0< b < 1) a  Se a > 1, a função é crescente, pois se x > y, então >
função é decrescente.
 Se 0 < a < 1, a função é decrescente pois se x < y, então
I) ( ) = >
x y Logaritmos Decimais

Vamos estudar os logaritmos em uma base
específica, a base 10.
Qualquer que seja o n° Real positivo x, ele estará
certamente compreendido entre duas potências de 10 com
expoentes inteiros e consecutivos.
Ex:
1. x = 0,04 ⤇ 10-2 < 0,04 <10-1
2. x = 3,72 ⤇ 100 < 3,72 < 101
3. x = 573 ⤇ 102 < 573 < 103

Assim, dado x > 0, existe c e Z tal que:

10c  x < 10c + 1 ⤇ log10c  log x < log 10c + 1, logo:

c  log x < c + 1, então podemos afirmar que:
log x = c + m, onde c  Z e 0  m < 1, o número inteiro c é a
II) ( ) = característica do logaritmo de x e o m é a mantissa do
logaritmo de x.
x y
Cálculo da Característica

1. A característica do logaritmo decimal de um n°
real x > 1 é igual ao n° de algarismos de sua parte inteira
menos 1.
log 2, 3 c=0
log 31,4789 c=1
log 204 c=2
log 4194,710 c=3

2. A característica do logaritmo decimal de um
número
0 < x < 1 é o oposto da quantidade de zeros que precedem o
primeiro algarismo significativo.
Ex:
Logaritmo Característica
log 0,2 c = -1
log 0,035 c = -2
Gráfico da Função Logarítmica log 0,00405 c = -3
log 0,00053 c = -4
y y
y = logax Mantissa

É obtida nas tábuas de logaritmos, e tem uma propriedade
1 importante: Os logaritmos de 2 números cujas representações
decimais diferem apenas pela posição da vírgula, tem
0 x
y = logax
Mantissas iguais.
0 1 x 1. log 54 = 1,7323
2. log 5,4 = 0,7323
a>1 0<a<1 3. log540 = 2,7323
4. log 0,000054 = -5 +0,7323 = -4,2677 = 5 ,7323

onde 5 é característica e 7323 é mantissa


a) 1, 50 c) 101, 200
Observe que no exemplo acima, dizemos que -4,2677 é a
forma negativa e 5 ,7323 é a forma mista ou preparada.
b) 51, 100 d) 201, 500
Questão 10) A figura a seguir mostra o gráfico da função
Exercícios logaritmo na base b.
O valor de b é:
Questão 1) Resolva os logaritmos a seguir:
a) 1/4 b) 2.

a) b) c) 3. d) 4.

c) d)

e) f)
Questão 11) A equação log 2 (9x-1 +7) = 2 + log 2 (3 x-1+1)
possui
g) h)
a) duas raízes positivas. c) duas raízes simétricas.
Questão 2) O gráfico que melhor representa a função b) duas raízes negativas. d) uma única raiz..
mostrada na figura adiante, é:
Questão 12) Se log 2 123 = 2,09, o valor de log 21,23 é:
a) 0,0209 b) 0,09 c) 0,209 d) 1,09

Questão 13) O valor da soma log(1/2) + log(2/3) + log(3/4) +
... + log(99/100) é:
a) 0 b) -1 c) -2 d) 2

Questão 14) Se a = log2(2 sen 70°/ cos 20°), então log‚ a é:
a) -1/2 b) -1/4 c) 1 d) -1

Questão 15) Se log 7 875 = a, então log 35 245 é igual a:
Questão 3) log 32= x, então3 x + 3-x é:
a) (a + 2)/(a + 7) b) (a + 2)/(a + 5)
a) 9/7 c) (a + 5)/(a + 2) d) (a + 7)/(a + 2)
b) 5/2
c) 4 Questão 16) Na figura abaixo, a curva representa o gráfico
d) 6 da função y  log x , para x  0 . Assim, a soma das áreas
das regiões hachuradas é igual a
Questão 4) Se log x2 = ¼, então a base x vale:
y
a) 20 b) 16 c) 12 d) 10
a) log 2 S2
S1
Questão 5) O valor de 4 log29 é: b) log 3
c) log 4
a) 81 b) 9 c) 64 d) 36
d) log 6
1000
Questão 6) Seja x = 2 sabendo que log 10 é 2 1 2 3 4 x
aproximadamente 0,30103 pode-se afirmar que o n° de
algarismos de x é:

a) 300 c) 1000 Questão 17) O valor de y  IR que satisfaz a igualdade
b) 301 d) 2000
log y 49 = log y 2 7  log 2 y 7 ,é
Questão 7) Calcule o valor da expressão
a) ½ b) 1/3 c) 3 d) 1/8
log n  log n n
 n
n

  Questão 18) Resolvendo o sistema, obtemos
a) 2 b) -2 c) 4 d) n log 2 x  log 4 y  4

 xy  8
Questão 8) O número real x que satisfaz a equação  1 
S   32 , 
log2 (12 – 2x) = 2x é:  4  c) S   2 , 4 
a)
 1 
a) log2 5 b) 2 c) log 25 d) log 23 S   16 ,  
b) S  8 , 1  d)  2 
Questão 9) Se o logarítimo de um número na base “n” é 4 e
na base “ n 2 ” é 8, então esse número está no intervalo



Questão 19) Se log 3 2 = a e log73 = b, então log314 = Questão 24) A intensidade I de um terremoto, medida pela
escala Richter, é definida pela equação a seguir, na qual E
a 1 ab  1 ab  1 representa a energia liberada em kWh.
a)
b 1 b) c) d) O gráfico que melhor representa a energia E, em função da
a b b a intensidade I, sendo E0 igual a 10-3 kWh, está indicado em:
Questão 20) Supondo que exista, o logaritmo de a na base b
é:

a) o número ao qual se eleva a para se obter b.
b) o número ao qual se eleva b para se obter a.
c) a potência de base b e expoente a.
d) a potência de base a e expoente b.
e) a potência de base 10 e expoente a.

Questão 21) (Unicamp) Um capital de R$12.000,00 é
aplicado a uma taxa anual de 8%, com juros capitalizados
anualmente. Considerando que não foram feitas novas
aplicações ou retiradas, encontre:

a) O capital acumulado após 2 anos.
b) O número inteiro mínimo de anos necessários para que o
capital acumulado seja maior que o dobro do capital inicial.
[Se necessário, use log2 = 0,301 e log3 = 0,477].

Questão 22) O brilho de uma estrela percebido pelo olho
humano, na Terra, é chamado de magnitude aparente da
estrela. Já a magnitude absoluta da estrela é a magnitude
aparente que a estrela teria se fosse observada a uma
distância padrão de 10 parsecs (1 parsec é aproximadamente
3 × 1013 km). As magnitudes aparente e absoluta de uma
estrela são muito úteis para se determinar sua distância ao
planeta Terra. Sendo m a magnitude aparente e M a
magnitude absoluta de uma estrela, a relação entre m e M é
dada aproximadamente pela fórmula

M = m + 5 . logƒ (3 .d-0,48)

onde d é a distância da estrela em parsecs. A estrela Rigel
tem aproximadamente magnitude aparente 0,2 e magnitude
absoluta - 6,8. Determine a distância, em quilômetros, de
Rigel ao planeta Terra.

Questão 23) Na figura a seguir, encontram-se representados
o gráfico da função f : ]0,-∞[ → IR, definida por f(x) = log2x,
e o polígono ABCD. Os pontos A, C e D estão sobre o
gráfico de f. Os pontos A e B estão sobre o eixo das
abscissas. O ponto C tem ordenada 2, o ponto D tem abscissa
2 e BC é perpendicular ao eixo das abscissas.

Sabendo que os eixos estão graduados em centímetros, a área
do polígono ABCD é:
a) 2,5 cm2.
b) 3 cm2.
c) 3,5 cm2.
d) 4 cm2.
e) 4,5 cm2.


Função exponencial logaritmo_2012

Mais conteúdo relacionado

Mais procurados

Semelhante a Função exponencial logaritmo_2012

Mais de cristianomatematico

Último

Função exponencial logaritmo_2012