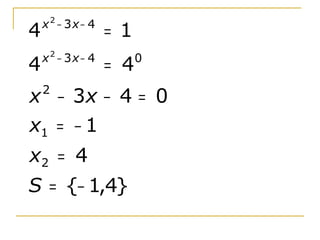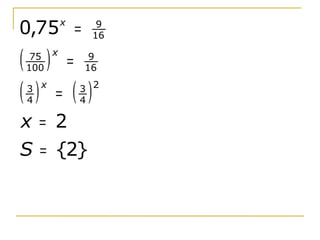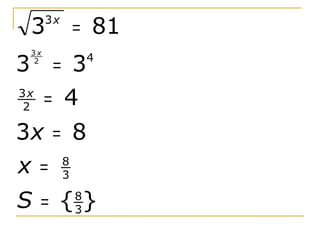Uma equação exponencial contém uma incógnita no expoente de uma potência. Resolve-se transformando as bases em iguais e usando a propriedade de que a função exponencial é injetora. Exemplos mostram resoluções de equações exponenciais simples e com artifícios de cálculo como mudança de variável. Exercícios são propostos no final.

1. Equação Exponencial
Prof. Miguel
Matemática2

2. Equação exponencial é toda equação
que apresenta a incógnita no expoente de
uma ou mais potências de base positiva e
diferente de 1.
5 = 25
x
9 − 3 = 6
x x
2 = 5
x

3. Resolução
 Primeiramente transformamos as bases em bases
iguais. (Fatorando)
 Usamos o fato de que a função exponencial é
injetora, daí temos
a x1
= a x2
⇔ x1 = x2

4. Exemplos simples
3 x− 1
= 81
3 x− 1
= 3 4
x− 1= 4
x = 5
S = {5}

5. x2 − 3x − 4
4 = 1
x2 − 3x − 4 0
4 = 4
2
x − 3x − 4 = 0
x1 = − 1
x2 = 4
S = {− 1,4}

6. 0,75 = x 9
16
( ) =
75 x
100
9
16
( ) = ( )
3 x
4
3 2
4
x = 2
S = {2}

7. 3 3x
= 81
3x
3 2
= 3 4
3x
2 = 4
3x = 8
x = 3
8
S= { } 8
3

8. Exemplos que usam artíficios de cálculos
3⋅ 4 x+ 1
= 96
2 x+ 2
+ 2 x− 1
= 18
2 2x
− 9⋅2 + 8 = 0 x

9. 3⋅ 4 x+ 1
= 96 2x = 3
4 x+ 1
= 96
3
x = 2
3
4 x+ 1
= 32 S= {}
3
2
(2 )2 x+ 1
= 2 5
2 = 2
2x+ 2 5
2x + 2 = 5

10. 2 x + 2 + 2 x − 1 = 18
Pela propriedade am ⋅ an = am+ n e am ÷ an = am− n
2 ⋅2 +
x 2 2x
21
= 18
Pode - se efutuar mudança de variável 2 x = a
4a + 2 = 18
a
8 a + a = 36
2 Voltando a variável
9a = 36
2 = 4
x
a= 4
2 x = 22
x = 2
S = {2}

11. 22 x − 9 ⋅ 2 x + 8 = 0
Pela propriedade ( a )
m n
= a mn
(2 )
x 2
− 9 ⋅ 2x + 8 = 0
Pode - se fazer a mudança variável 2 x = m
m2 − 9m + 8 = 0
m1 = 1
m2 = 8

12. Voltando a variável
2x = 1
2 x = 20
x = 0
2x = 8
2 x = 23
x = 3
S = {0,3}

13.  x y 1
2 ⋅ 4 =
 2
 7x+ y = 1


14. Exercícios
Página 214: 31, 32, 34, 36 e 38

15. Referências
PAIVA, Manoel Rodrigues. Matemática 1. 1ª edição. São Paulo:
Moderna, 2009.
Conexões com a matemática/ editora responsável Juliane
Matsubara Barroso; obra coletiva concebida, desenvolvida e
produzida pela editora Moderna. 1ª edição. São Paulo: Moderna,
2010.