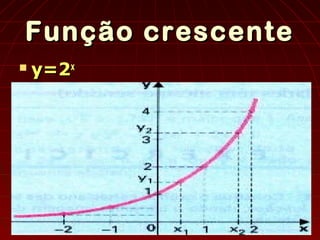
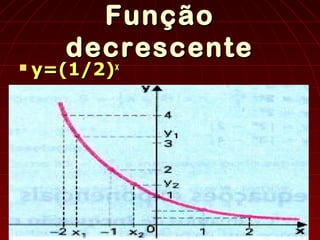
O documento discute funções exponenciais, definindo-as como funções onde a variável aparece em expoente. Apresenta seus domínios e contradomínios, características gráficas como nunca interceptar o eixo x e sempre ser positiva, e métodos para resolver equações e inequações exponenciais.

1. Função
Função
Exponencial
Exponencial
Prof. Gledson Guimarães
Prof. Gledson Guimarães

2. Definição
Definição
 Chamamos de
Chamamos de
funções
funções
exponenciais
exponenciais
aquelas nas
aquelas nas
quais temos a
quais temos a
variável
variável
aparecendo
aparecendo
em expoente.
em expoente.
 A função
A função f:IR
f:IR
IR
IR+
+
definida por
definida por
f(x)=a
f(x)=ax
x
, com a
, com a ∈
∈
IR
IR+
+ e
e a
a≠
≠1
1, é
, é
chamada
chamada função
função
exponencial de
exponencial de
base
base a
a.
.

3. Domínio e
Domínio e
Contradomínio
Contradomínio
 O
O domínio
domínio dessa função é
dessa função é
o conjunto IR (reais) e o
o conjunto IR (reais) e o
contradomínio
contradomínio é
é IR
IR+
+
(reais positivos, maiores
(reais positivos, maiores
que zero).
que zero).

4. GRÁFICO CARTESIANO
GRÁFICO CARTESIANO
DA EXPONENCIAL
DA EXPONENCIAL
 Temos 2 casos a considerar:
Temos 2 casos a considerar:

 quando a>1;
quando a>1;
Exemplo:
Exemplo: y=2
y=2x
x
(nesse caso, a=2, logo
(nesse caso, a=2, logo
a>1)
a>1)

 quando 0<a<1
quando 0<a<1.
.
Exemplo:
Exemplo: y=(1/2)
y=(1/2)x
x
(nesse caso, a=1/2,
(nesse caso, a=1/2,
logo 0<a<1)
logo 0<a<1)

5. Função crescente
Função crescente
 y=2
y=2x
x

6. Função
Função
decrescente
decrescente
 y=(1/2)
y=(1/2)x
x

7. Características Gráficas
Características Gráficas
 o gráfico
o gráfico nunca
nunca intercepta o
intercepta o
eixo
eixo horizontal
horizontal;
; a função não
a função não
tem raízes
tem raízes;
;
 o gráfico
o gráfico corta
corta o
o eixo vertical
eixo vertical
no
no ponto (0,1)
ponto (0,1);
;
 os valores de y são
os valores de y são sempre
sempre
positivos,
positivos, portanto o
portanto o
conjunto imagem é Im=IR+.
conjunto imagem é Im=IR+.

8. EQUAÇÕES
EQUAÇÕES
EXPONENCIAIS
EXPONENCIAIS
 Para resolver equações exponenciais,
Para resolver equações exponenciais,
devemos realizar dois passos
devemos realizar dois passos
importantes:
importantes:
 1º) redução dos dois membros da
1º) redução dos dois membros da
equação a potências de mesma
equação a potências de mesma
base;
base;
 2º) aplicação da propriedade
2º) aplicação da propriedade :
:
)
0
1
( >
≠
=
⇒
= a
e
a
n
m
a
a n
m

9. Exemplos de
Exemplos de
equações
equações
 3
3x
x
=81 (x=4)
=81 (x=4)
 9
9x
x
= 1
= 1
 2
23x-1
3x-1
= 32
= 322x
2x
 3
32x
2x
–6.3
–6.3x
x
–27=0
–27=0

10. Resoluções
Resoluções
 3
3x
x
=81
=81
81=3
81=34
4
logo 3
logo 3x
x
= 3
= 34
4
x=4
x=4
S = {4}
S = {4}

11. Resoluções
Resoluções
 9
9x
x
= 1
= 1
9
9x
x
= 1
= 1 ⇒
⇒ 9
9x
x
= 9
= 90
0
; logo
; logo
x=0.
x=0.
S = {0}
S = {0}

12. Resoluções
Resoluções
 2
23x-1
3x-1
= 32
= 322x
2x
2
23x-1
3x-1
= 32
= 322x
2x
2
23x-1
3x-1
= (2
= (25
5
)
)2x
2x
2
23x-1
3x-1
= 2
= 210x
10x
3x-1=10x
3x-1=10x
x=-1/7 S = {-1/7 }
x=-1/7 S = {-1/7 }

13. Resoluções
Resoluções
 3
32x
2x
–6.3
–6.3x
x
–27=0
–27=0
3
32x
2x
–6.3
–6.3x
x
–27=0
–27=0
(3
(3x
x
)
)2
2
-6.3
-6.3x
x
–27=0
–27=0 Fazendo 3
Fazendo 3x
x
=y,
=y,
y2-6y–27=0
y2-6y–27=0
aplicando Bhaskara encontramos
aplicando Bhaskara encontramos y’=
y’=
-3 e y’’= 9
-3 e y’’= 9
Para achar o x, devemos voltar os valores
Para achar o x, devemos voltar os valores
para a equação auxiliar 3x = y:
para a equação auxiliar 3x = y:
y’= -3
y’= -3 ⇒
⇒ 3x’ = -3
3x’ = -3 ⇒
⇒ não existe x’, pois
não existe x’, pois
potência de base positiva é positiva
potência de base positiva é positiva
y’’= 9
y’’= 9 ⇒
⇒ 3x’’ = 9
3x’’ = 9 ⇒
⇒ 3x’’ = 32
3x’’ = 32 ⇒
⇒ x’’=2
x’’=2

14. Inequações
Inequações
Exponenciais
Exponenciais
 A resolução de inequações
A resolução de inequações
exponenciais tem dois passos
exponenciais tem dois passos
importantes:
importantes:
 1º) redução dos dois membros da
1º) redução dos dois membros da
inequação a potências de mesma
inequação a potências de mesma
base;
base;
 2º) aplicação da propriedade:
2º) aplicação da propriedade:

15. Inequações
Inequações
Exponenciais
Exponenciais

a>1
a>1 a
am
m
> a
> an
n
⇒
⇒ m>n
m>n
(as desigualdades têm mesmo
(as desigualdades têm mesmo
sentido)
sentido)

0<a<1
0<a<1 a
am
m
> a
> an
n
⇒
⇒ m<n
m<n
(as desigualdades têm sentidos ≠)
(as desigualdades têm sentidos ≠)

16. Exemplo
Exemplo
negativos)
(reais
IR
S
Portanto
x
:
obtemos
1,
que
maior
é
(4)
base
a
Como
Porém,
daí,
e
-
:
seja
ou
,
:
temos
4
por
lados
os
ambos
ndo
Multiplica
4
escrita
ser
pode
inequação
A
:
Resolução
-
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
=
<
⇒
<
<
⇒
<
<
−
>
⇒
−
>
−
+
−
>
−
+
−
>
−
+
−
>
−
+ +
−
0
4
4
.
4
4
1
4
1
4
11
4
.
11
11
4
).
16
4
1
(
11
4
.
16
4
.
4
4
.
4
11
4
.
4
4
4
4
11
4
4
4
)
1
0
0
1
1