Matrizes 17122016
•Transferir como PPT, PDF•
5 gostaram•421 visualizações
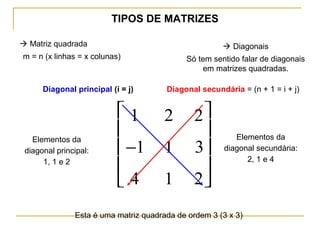
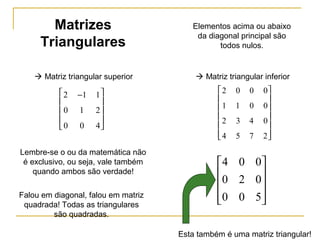
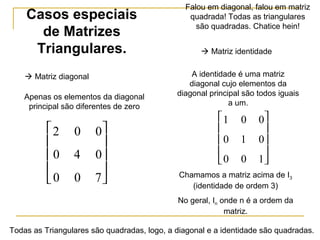
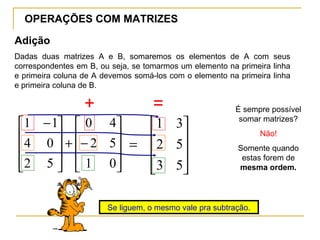
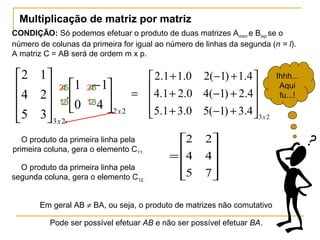
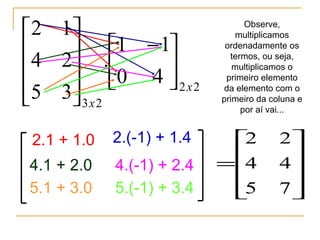
O documento define matrizes e apresenta seus principais tipos e operações. São definidas matrizes quadradas, triangulares, nulas, identidade e diagonal. São explicadas operações como adição, subtração, multiplicação por escalar e multiplicação de matrizes. Por fim, são apresentados exemplos ilustrativos.
![Definição de Matrizes
Matriz: Tabela de elementos dispostos em linhas e colunas.
Amxn
=
a a a
a a a
a a a
n
n
m m mn
11 12 1
21 22 2
1 2
= [aij
]mxn
matriz A de m linhas e n colunas
Elemento da linha i
e coluna j
Elemento da 2 ª linha e 1ª coluna](https://image.slidesharecdn.com/matrizes-17122016-161217172745/85/Matrizes-17122016-1-320.jpg)
Recomendados
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Destaque
Destaque (9)
Semelhante a Matrizes 17122016
Semelhante a Matrizes 17122016 (20)
Mais de Antonio Carneiro
Mais de Antonio Carneiro (20)
Último
Último (20)
Matrizes 17122016
- 1. Definição de Matrizes Matriz: Tabela de elementos dispostos em linhas e colunas. Amxn = a a a a a a a a a n n m m mn 11 12 1 21 22 2 1 2 = [aij ]mxn matriz A de m linhas e n colunas Elemento da linha i e coluna j Elemento da 2 ª linha e 1ª coluna
- 2. TIPOS DE MATRIZES 1 2 2 1 1 3 4 1 2 − Matriz quadrada m = n (x linhas = x colunas) Esta é uma matriz quadrada de ordem 3 (3 x 3) Diagonais Só tem sentido falar de diagonais em matrizes quadradas. Diagonal principal (i = j) Diagonal secundária = (n + 1 = i + j) Elementos da diagonal principal: 1, 1 e 2 Elementos da diagonal secundária: 2, 1 e 4
- 3. 2 1 1 0 1 2 0 0 4 − Matriz triangular superior Matrizes Triangulares 2 0 0 0 1 1 0 0 2 3 4 0 4 5 7 2 Matriz triangular inferior 500 020 004 Elementos acima ou abaixo da diagonal principal são todos nulos. Lembre-se o ou da matemática não é exclusivo, ou seja, vale também quando ambos são verdade! Esta também é uma matriz triangular! Falou em diagonal, falou em matriz quadrada! Todas as triangulares são quadradas.
- 4. Casos especiais de Matrizes Triangulares. Matriz identidade 2 0 0 0 4 0 0 0 7 1 0 0 0 1 0 0 0 1 Matriz diagonal Apenas os elementos da diagonal principal são diferentes de zero A identidade é uma matriz diagonal cujo elementos da diagonal principal são todos iguais a um. Falou em diagonal, falou em matriz quadrada! Todas as triangulares são quadradas. Chatice hein! Todas as Triangulares são quadradas, logo, a diagonal e a identidade são quadradas. Chamamos a matriz acima de I3 (identidade de ordem 3) No geral, In onde n é a ordem da matriz.
- 5. 0 0 0 0 0 0 0 0 0 0 0 0 Matriz nula Todos os elementos são nulos. Chamamos a matriz nula de Omxn Então essa é O3x4 A Matriz nula não precisa ser quadrada! Igualdade de Matrizes. Duas matrizes são ditas idênticas quando seus elementos correspondentes são iguais. − 421 213 112 − 421 213 112 Caso ao olhar essas duas matrizes e não ver que elas são iguais, favor procurar o oculista.
- 6. Transposta troca de linha por coluna (m x n => n x m ) 23 41 30 12 x A − = . 431 102 =A 32 t x − Matriz A transposta Simétrica Matriz quadrada tal que At = A 22 23 31 x A = . 23 31 =A 22 t x Matriz A transposta Anti-Simétrica Matriz quadrada tal que At = -A 33 013 102 320 x A −− − = . 013 102 320 =A 33 t x −− − = Os elementos da transposta são os opostos da original.
- 7. OPERAÇÕES COM MATRIZES Adição −+ − 01 52 40 52 04 11 = 53 52 31 Dadas duas matrizes A e B, somaremos os elementos de A com seus correspondentes em B, ou seja, se tomarmos um elemento na primeira linha e primeira coluna de A devemos somá-los com o elemento na primeira linha e primeira coluna de B. É sempre possível somar matrizes? Não! Somente quando estas forem de mesma ordem. + = Se liguem, o mesmo vale pra subtração.
- 8. Multiplicação por escalar Multiplicação por escalar ( número real qualquer) multiplicamos todos os elementos da matriz por este número. − − 31 102 .2 − −− = 3.21.2 10.22.2 − −− = 62 204 Matriz A Matriz -2A
- 9. Multiplicação de matriz por matriz CONDIÇÃO: Só podemos efetuar o produto de duas matrizes Amxn e Blxp se o número de colunas da primeira for igual ao número de linhas da segunda (n = l). A matriz C = AB será de ordem m x p. 22 23 40 11 . 35 24 12 x x − 23 4.3)1(50.31.5 4.2)1(40.21.4 4.1)1(20.11.2 x +−+ +−+ +−+ = = 75 44 22 Em geral AB ≠ BA, ou seja, o produto de matrizes não comutativo 2 1 2 1 4 2 4 2 5 3 5 3 Pode ser possível efetuar AB e não ser possível efetuar BA. O produto da primeira linha pela primeira coluna, gera o elemento C11. O produto da primeira linha pela segunda coluna, gera o elemento C12. Ihhh... Aqui fu...!
- 10. 22 23 40 11 . 35 24 12 x x − = 75 44 222.1 + 1.0 2.(-1) + 1.4 4.1 + 2.0 4.(-1) + 2.4 5.1 + 3.0 5.(-1) + 3.4 Observe, multiplicamos ordenadamente os termos, ou seja, multiplicamos o primeiro elemento da elemento com o primeiro da coluna e por aí vai...
- 11. EXEMPLO 1 1) Seja A = e seja B = . Calcule A + B. 11
- 12. EXEMPLO 2 2) Seja A = e seja B = . Calcule A – B. 12
- 13. EXEMPLO 3 3) Calcule o produto das matrizes: 13
- 14. EXEMPLO 4 4) A mátriz A de ordem 2 x 3 definida por dada por: a) b) c) d) e) 14
- 15. EXEMPLO 5 5) Dadas as matrizes calcule a matriz A – Bt é: 15
- 16. Professor Antônio Carlos Carneiro Barroso Graduado Em Matemática pela UFBA Graduado em Ciências naturais pela UFBA Pós graduado em Metodologia e Didática de ensino Superior www.ensinodematemtica.blogspot.com.br www.youtube.com/accbarroso www.facebook.com/acmatematico www.twitter.com/profbarroso Salvador-Ba