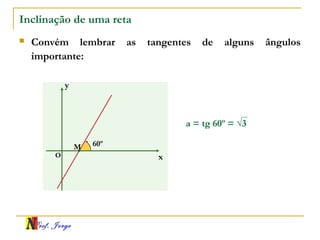
Este documento fornece informações sobre o estudo de retas no plano cartesiano, incluindo: 1) Como representar pontos e traçar retas no plano cartesiano usando coordenadas cartesianas. 2) Como escrever a equação geral de uma reta e as equações de retas paralelas aos eixos. 3) Como calcular a inclinação de uma reta e classificar o ângulo de inclinação. 4) Como escrever a equação de uma reta na forma reduzida a partir de sua inclinação e um ponto.

1. Prof. Jorge
Antonio Carlos Carneiro Barroso
www.ensinodematemtica.blogspot.com.br
www.profantoniocarneiro.com
Professor de Matemática
Colégio Estadual Dinah Gonçalves
Valéria-Salvador-Bahia

2. Prof. Jorge
Estudo da reta

3. Prof. Jorge
x
y
O (0, 0)
1º quadrante2º quadrante
3º quadrante 4º quadrante
eixo das
abscissas
eixo das ordenadas
Origem
Plano cartesiano

4. Prof. Jorge
P
x
y
O
4
3
P(3, 4)
Coordenadas no plano
 3 é a abscissa de P;
 4 é a ordenada de P;
 3 e 4 são as coordenadas
de P;
P(x, y)
 Em geral:

5. Prof. Jorge
Sinais no plano
x
y
+
+
++
–
–
– –
y = 0
O( 0, 0)
x = 0

6. Prof. Jorge
Bissetrizes no plano
x
y
y = xy = –x
1ª bissetriz2ª bissetriz

7. Prof. Jorge
Equação da reta

8. Prof. Jorge
Equação geral da reta
 A toda reta contida no sistema xOy de coordenadas
cartesianas está associada uma equação de 1.º grau, nas
variáveis x e y. Essa equação se verifica para todos os
pontos da reta, e só eles.
Retas paralelas aos eixos;
Retas não-paralelas aos eixos;

9. Prof. Jorge
Retas paralelas aos eixos
 A figura mostra duas retas r e s, contidas no plano
cartesiano xOy.
x
y
O 4
2
r
s
 Equação da reta r: x = 4
 Equação da reta s: y = 2

10. Prof. Jorge
Retas paralelas ao eixo y
 A figura mostra três retas r, s e t, contidas no plano
cartesiano xOy.
x
y
O 3–2
r s  Equação de r: x = –2
1
t
 Equação de s: x = 1
 Equação de t: x = 3
 Geral: retas ∕∕ eixo y:
x = k
 k é a abscissa do ponto em que a reta intercepta o eixo x.

11. Prof. Jorge
Retas paralelas ao eixo x
 A figura mostra três retas w, u e p, contidas no plano
cartesiano xOy.
x
y
O
3
–1 p
u
 Equação de w: y = 3
2
w  Equação de u: y = 2
 Equação de p: y = –1
 Geral: retas ∕∕ eixo x:
y = h
 h é a ordenada do ponto em que a reta intercepta o eixo y.

12. Prof. Jorge
Retas não-paralelas aos eixos
 A figura mostra a reta r, contidas no plano cartesiano xOy,
determinada pelos pontos A(2, 1) e B(3, 3).
x
y
O 3
1
r
2
3
P(x, y) ∊ AB A, B e P estão⇒
alinhados
x y 1
1 2 1
3 3 1
= 0
x + 3y + 6 – 3 – 3x – 2y = 0
⇒ y – 2x + 3 = 0
A
B
P(x, y)

13. Prof. Jorge
Equação geral da reta
 Toda reta do plano cartesiano xOy está associada a uma
equação de 1.º grau Ax + By + C = 0, com A, B e C reais,
sendo A ≠ 0 ou B ≠ 0.
 A equação de uma reta pode ser escrita de infinitas formas,
todas equivalentes.
 2x – y – 3 = 0
 4x – 2y – 6 = 0
 6x – 3y – 9 = 0 ... e assim por diante.
 Cada uma dessas igualdades é uma equação geral da reta.

14. Prof. Jorge
Exemplos
 Traçar no plano cartesiano xOy, a reta r de equação geral
3x + 2y – 5 = 0.
x = 1 ⇒ 3.1 + 2y – 5 = 0 ⇒ 2y = 2 ⇒ y = 1
x = 3 ⇒ 3.3 + 2y – 5 = 0 ⇒ 2y = –4 ⇒ y = –2
x
y
O
3
1
r
–2
1

15. Prof. Jorge
Exemplos
 Analisar se M(2, –1) e N(3, 5) são pontos da reta de
equação geral 5x + y – 9 = 0.
⇒ 5.2 + (–1) – 9 = 0
 Para que cada ponto pertença à reta, suas coordenadas devem
satisfazer a equação.
M(2, –1) ⇒ 10 –1 – 9 = 0 ⇒ 0 = 0
⇒ 5.3 + 5 – 9 = 0N(3, 5) ⇒ 15 + 5 – 9 = 0 ⇒ 11 ≠ 0
 Concluímos que M é ponto da reta dada, mas N não é.

16. Prof. Jorge
Inclinação de uma reta

17. Prof. Jorge
40 m
Inclinação de uma reta
 Imagine um carro subindo uma rampa reta, conforme
figura. Suponha que para cada 40 m percorridos na
horizontal, a pista se eleve 6 m.
40 m
6 m
α
 O ângulo α que a rampa forma com a horizontal é o ângulo
de inclinação da rampa. O valor de tg α é a inclinação da
rampa.
6 mInclinação = tg α = = 0,15 = 15 %

18. Prof. Jorge
Inclinação de uma reta
 Vamos analisar agora duas situações extremas.
 Quando o carro percorre um trecho horizontal, dizemos que
a rampa tem inclinação 0 e que o ângulo de inclinação é 0º.
(tg 0o
= 0).
α = 0o
⇒ Inclinação = tg α = tg 0o
= 0

19. Prof. Jorge
Inclinação de uma reta
 Vamos analisar agora duas situações extremas.
 O auto não sobe uma rampa vertical. Nesse
caso, não se define a inclinação da rampa e o
ângulo de inclinação é 90º. (tg 90º = Não é
definido).
α = 90o
⇓
Inclinação não se define.

20. Prof. Jorge
Q
Inclinação de uma reta
 Considere uma reta r, não paralela aos eixos x e y, contida
no plano cartesiano xOy.
x
y
O
yQ
yP
xQxP
P
αM
xQ – xP
yQ – yP
Inclinação = tg α
α
yQ– yP
xQ– xP
a = tg α =
∆x
∆y
a =
r

21. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
a = tg 30º =
x
y
O
30ºM
3
√3

22. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
a = tg 45º = 1
x
y
O
45ºM

23. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
a = tg 60º = √3
x
y
O
60ºM

24. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
x
y
O
120º
M
a = tg 120º = – tg 60º = –√3

25. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
a = tg 135º = – tg 45º = – 1
x
y
O
135º
M

26. Prof. Jorge
Inclinação de uma reta
 Convém lembrar as tangentes de alguns ângulos
importante:
a = tg 150º = – tg 30º =
x
y
O
150º
M
3
–√3

27. Prof. Jorge
Exemplos
 Em cada caso, obter a inclinação e classificar o ângulo α de
inclinação da reta MN.
x
y
O
α
M
N
–2 1
3
5
xN – xM
yN – yM
a = tg α =
1 – (–2)
5 – 3
a =
3
2
a =
a > 0 e α é agudo
(α < 90º)
a) M(–2, 3) e N(1, 5)

28. Prof. Jorge
Exemplos
 Em cada caso, obter a inclinação e classificar o ângulo α de
inclinação da reta MN.
x
y
O
α
M
N
–2
3
3
xN – xM
yN – yM
a = tg α =
3 – (–2)
–1 – 3
a =
5
– 4
a =
a < 0 e α é obtuso
(90º < α < 180º)
b) M(–2, 3) e N(3, –1)
–1

29. Prof. Jorge
Exemplos
 Em cada caso, obter a inclinação e classificar o ângulo α de
inclinação da reta MN.
x
y
O
M N
–1 3
3
xN – xM
yN – yM
a = tg α =
1 – (–1)
3 – 3
a =
a = 0
a = 0 ⇒ α = 0º (nulo)
c) M(–1, 3) e N(2, 3)

30. Prof. Jorge
Exemplos
 Em cada caso, obter a inclinação e classificar o ângulo α de
inclinação da reta MN.
x
y
O
M
N
–1
2
3
xN – xM
yN – yM
a = tg α =
2 – 2
3 – (–1)
a =
a = não é definida
α = 90º (reto)
d) M(2, –1) e N(2, 3)
α
⇓

31. Prof. Jorge
Inclinação de uma reta - resumo
 O ângulo de inclinação α de uma reta é tal que 0º ≤ α ≤ 180º.
 Sua inclinação a pode ser positiva, negativa ou nula,
conforme a medida do ângulo α (α ≠ 90º).
 α = 0º ⇔ a = 0.
 0º < α < 90º ⇔ a > 0.
 α = 90º a inclinação⇔ a não é definida.
 90º < α < 180º ⇔ a < 0.

32. Prof. Jorge
Exemplos
 Achar as inclinações das retas r, s e t da figura abaixo.
x
y
O
120º45º 45º
r s
t
 ar = tg 45º = 1
 as = tg 45º = 1  at = tg 120º – √3= – tg 60º =

33. Prof. Jorge
Equação reduzida da reta

34. Prof. Jorge
Equação reduzida da reta
 Uma reta é determinada, quando são dados sua inclinação e
um de seus pontos. Suponhamos no plano xOy, uma reta r
que passa por A(2, 3) e têm ângulo de inclinação α = 135º.
 Vamos obter a equação da reta r.
x
y
O
135º
A
2
3
M(x, y)
xM – xA
yM – yA
a = tg 135º = –1.
x – 2
y – 3
–1 =a =
y – 3 = –1(x – 2)
y – 3 = –1x + 2
y = –1x + 5
⇒
y = –x + 5

35. Prof. Jorge
Equação reduzida da reta – Caso Geral
 Suponhamos que uma reta r de inclinação a = tg α e que passe
pelo ponto P(xP, yP), como mostra a figura.
x
y
O
α
P
xP
yP
M (x, y)
xM – xA
yM – yA
x – xP
y – yP
a =a =
y – yP = a(x – xP)
⇒
⇒ y – yP = ax – axP ⇒ y = ax + (–axP + yP)
⇒ y = ax + b  Equação reduzida da reta

36. Prof. Jorge
Equação reduzida da reta
 Na equação reduzida y = ax + b, temos:
 Significa que a reta passa pelo ponto (0, b) → ponto do eixo y.
x = 0 ⇒ y = a.0 + b ⇒ y = b
 O coeficiente a é a inclinação da reta; ele é também chamado,
por isso, coeficiente angular da reta.
 O coeficiente b é a ordenada do ponto em que a reta corta o eixo
y; ele é chamado de coeficiente linear da reta.

37. Prof. Jorge
Exemplos
 Uma equação geral da reta r é 2x – y + 4 = 0. Escrever a
equação na forma reduzida, indicar os coeficientes angular
e linear e representar a reta no plano cartesiano xOy.
O coeficiente angular a = 2 e o coeficiente linear é b = 4.
2x – y + 4 = 0 ⇒ –y = –2x – 4 ⇒ y = 2x + 4
 a = 2, o ângulo de inclinação α < 90º.
 b = 4, a reta intercepta o eixo y no ponto (0, 4).
Vamos obter o ponto em que a reta corta o eixo x. Para isso, vamos
fazer y = 0.
y = 0 ⇒ 2x – 0 + 4 = 0 ⇒ 2x = –4 ⇒ x = –2 ⇒ (–2, 0)

38. Prof. Jorge
Exemplos
 Veja a representação da reta r: 2x – y + 4 = 0 no plano xOy.
x
y
O
r
–2
4
y = 2x + 4

39. Prof. Jorge
Exemplos
 O gráfico a seguir mostra uma reta s. Encontrar a equação
reduzida e uma equação geral para essa reta.
x
y
O
s
45º
2
y = ax + b
 A reta corta o eixo y no ponto
de ordenada 2, ponto (0, 2),
logo b = 2.
 α = 180º – 45º = 135º
a = tg 135º = –1.
y = – x + 2
⇒ x + y – 2 = 0
α

40. Prof. Jorge
Exemplos
 Achar a equação reduzida da reta r que passa pelos pontos
A(–2, 6) e B(1, –3).
xA – xB
yA – yB
–2 – 1
6 –(–3)
a =
∆x
∆y
= =
 Primeiro vamos calcular a inclinação da reta.
–3
9
= ⇒ a = –3
 Utilizando o ponto A(–2, 6), por exemplo, obtemos a equação
fundamental, em seguida a equação reduzida da reta.
y – yP = a(x – xP) ⇒ y – 6 = –3(x + 2)
⇒ y – 6 = –3x – 6 ⇒ y = –3x