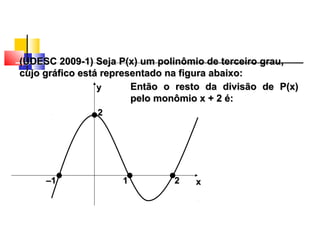
O documento apresenta os conceitos básicos de polinômios, incluindo: (1) definição de polinômio como uma soma de monômios; (2) operações com monômios e polinômios como adição, subtração, multiplicação e divisão; (3) grau de um polinômio; (4) raízes de equações polinomiais.

1. Polinômios
( ) n
nnn
axaxaxaxP ++++= −−
...2
2
1
10
DefiniçãoDefinição
Soma de monômiosSoma de monômios
naaaa ,...,,, 210
Números ComplexosNúmeros Complexos
CoeficientesCoeficientes
...,2,1, −− nnn ExpoentesExpoentes
Números NaturaisNúmeros Naturais

2. ( ) n
nnn
axaxaxaxP ++++= −−
...2
2
1
10
Variável Pode assumir valoresPode assumir valores
ComplexosComplexos
na Termo independente de xTermo independente de x
x
Polinômios
DefiniçãoDefinição
Soma de monômiosSoma de monômios

3. ( ) 78
510 xxxP −=
( ) 5
2
3
53 78
−+−−=
x
xxxP
( ) 2
2
3
54 23
−+−−=
x
ixxxP
Polinômios
São PolinômiosSão Polinômios

4. ( ) 25 2
−+−= xxxxF
( )
12
15
23
−+−
−
=
xxx
xF
( ) 5
4321
234
+−+−=
xxxx
xF
Polinômios
Não são PolinômiosNão são Polinômios

5. ( ) 254 23
−+−= xxxxP
Valor NuméricoValor Numérico
( ) ?2 =−P
( ) ( ) ( ) ( ) 2225242
23
−−+−−−=−P
( ) ( ) ( ) 2245842 −−−−=−P
( ) 2220322 −−−−=−P
( ) 562 −=−P
Polinômios

6. ( )1P Fornece o valor da soma dosFornece o valor da soma dos
coeficientes do polinômio P(x).coeficientes do polinômio P(x).
( )0P Fornece o valor do termoFornece o valor do termo
independente de x.independente de x.
Polinômios
Valor NuméricoValor Numérico

7. ( ) 234
16164 xxxxP ++=
16164 ++=Soma
36=Soma
( ) ( )22
42 xxxP +=
Qual a soma dosQual a soma dos
coeficientes docoeficientes do
polinômio P(x).polinômio P(x).
Polinômios
Valor NuméricoValor Numérico

8. ( ) ( ) ( )[ ]22
14121 +=P
( ) ( )2
421 +=P
( ) ( ) 3661
2
==P Soma dosSoma dos
coeficientecoeficiente
ss
( ) ( )22
42 xxxP +=
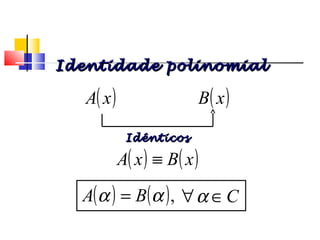
Polinômios
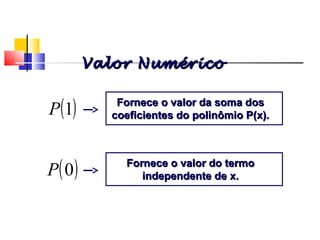
Valor NuméricoValor Numérico
Qual a soma dosQual a soma dos
coeficientes docoeficientes do
polinômio P(x).polinômio P(x).

9. ( ) ( )3
52 −= xxP
125−
( ) 125150608 23
−+−= xxxxP
Qual o valor doQual o valor do
termotermo
independente deindependente de
x.x.
Termo independenteTermo independente
de xde x
Polinômios
Valor NuméricoValor Numérico

10. ( ) ( )[ ]3
5020 −=P
( ) ( )3
500 −=P
( ) ( )3
50 −=P
( ) 1250 −=P
TermoTermo
independente deindependente de
xx
Polinômios
Valor NuméricoValor Numérico
( ) ( )3
52 −= xxP
Qual o valor doQual o valor do
termotermo
independente deindependente de
x.x.

11. ( ) 0=αP
( ) 654
−−= xxxP
( ) ( ) ( ) 62522
4
−−=P
( ) 610162 −−=P
( ) 02 =P
Raiz de um polinômioRaiz de um polinômio
αα é raiz do polinômioé raiz do polinômio
P(x).P(x).
2 é raiz do2 é raiz do
polinômiopolinômio
P(x)P(x)
Polinômios

12. ( ) ( ) 422
2
+= iiP
( ) 442 2
+= iiP
( ) 02 =iP
( ) ( ) 4142 +−=iP
( ) 0=αP αα é raiz do polinômioé raiz do polinômio
P(x).P(x).
( ) 42
+= xxP
2i é raiz do2i é raiz do
polinômiopolinômio
P(x)P(x)
Raiz de um polinômioRaiz de um polinômio
Polinômios

13. ( ) 0...000 21
++++= −− nnn
xxxxP
Não se define grauNão se define grau
para um polinômiopara um polinômio
nulonulo
Polinômio NuloPolinômio Nulo
Polinômios

14. ( ) n
nnn
axaxaxaxP ++++= −−
...2
2
1
10
00 ≠a
( ) nPgr =
Grau de um PolinômioGrau de um Polinômio
Polinômios

15. ( ) 1536 234
+−++= xxxxxP
( ) 124 −= xxP
( ) 12−=xP
( ) 4=Pgr
( ) 1=Pgr
( ) 0=Pgr
Grau de um PolinômioGrau de um Polinômio
Polinômios

16. yx2
6
23
yx
x7
( ) 5=Pgr
Observação:Observação:
Monômio de grau 3: (2Monômio de grau 3: (2
+ 1)+ 1)
Monômio de grau 5: (3Monômio de grau 5: (3
+ 2)+ 2)
Monômio de grau 1Monômio de grau 1
( ) xyxyxxP 76 232
++=
Grau de um PolinômioGrau de um Polinômio
Polinômios

17. ( )xA
( ) ( )xBxA ≡
IdênticosIdênticos
( )xB
( ) ( ),αα BA = C∈∀α
Identidade polinomialIdentidade polinomial
Polinômios

18. ( ) ( ) ( ) 115204 323452
+−+−++−= xnxxxxmxP
( ) ( ) 1752512 2345
++−+−+= xxxxqxxB
1) Se e1) Se e( ) ( ) ( ) 11524 32352
+−+−+−= xnxxxmxP
qenm,
( ) ( ) 1752512 2345
++−+−+= xxxxqxxB
são polinômiossão polinômios idênticos, então a soma dos valoresidênticos, então a soma dos valores
positivos de é:positivos de é:
Polinômios

19. 




=−
=−
=−
05
71
124
3
2
q
n
m 1242
=−m
162
=m
4±=m
4=m
713
=−n
83
=n
2=n
05 =−q
5=q
524 ++=++ qnm
11=++ qnm
Polinômios

20. Operações com
Monômios e Polinômios

21. Adição de MonômiosAdição de Monômios
Devemos efetuar a soma ou subtração dos
coeficientes numéricos entre os monômios
semelhantes.
Ex:
= 12x2
– 2ay3
5x2
– 3ay3
+ 7x2
+ ay3
5x2
+ 7x2
– 3ay3
+ ay3
Monômios semelhantes Monômios semelhantes

22. Multiplicação de
Monômios
O produto de monômios é obtido da seguinte forma:
• em seguida, multiplicam-se as partes literais.
Ex: (4ax2
) . (–13a3
x5
) =
(4) . (–13) . (a1
. a3
) . (x2
. x5
) =
– 52a4
x7
• primeiro, multiplicam-se os coeficientes numéricos;

23. Lembrando...
Um produto de potências de mesma base pode
ser escrito na forma de uma única potência:
conservamos a base e adicionamos os
expoentes.
am
.an
= am+n
Ex: x4
.x9
= x4+9
= x13

24. Divisão de Monômios
A divisão de monômios é obtida da seguinte
forma:
• primeiro, dividem-se os coeficientes
numéricos;
• em seguida, dividem-se as partes literais.

25. Lembrando...
Um quociente de potências de mesma base
pode ser escrito na forma de uma única
potência: conservamos a base e subtraímos
os expoentes.
am
:an
= am–n
Ex: x12
: x8
= x12–8
= x4
*com a ≠ 0

26. Adição de Polinômios
Efetue a soma algébrica dos monômios semelhantes.
Ex:
(4x2
– 7x + 2) + (3x2
+ 2x + 3) – (2x2
– x + 6) =
= 4x2
– 7x + 2 + 3x2
+ 2x + 3 – 2x2
+ x – 6 =
→ eliminando os parênteses
= 4x2
+ 3x2
– 2x2
– 7x + 2x + x + 2 + 3 – 6 =
→ agrupando os termos semelhantes
= 5x2
– 4x – 1 → forma reduzida
* Não esqueça da regra
de sinais!

27. Multiplicação de Monômio
por Polinômio
A multiplicação de um monômio por um polinômio
é feita multiplicando-se o monômio por cada
termo do polinômio.
= 8x5
y3
– 20x3
y7
Ex:
4x2
y3
. (2x3
– 5xy4
) =
= 4x2
y3
. 2x3
+ 4x2
y3
. (– 5xy4
)
* Não esqueça da regra
de sinais!

28. A multiplicação de um polinômio por outro
polinômio é feita multiplicando-se cada termo
de um deles pelos termos do outro e, sempre
que possível, reduzindo os termos semelhantes.
Ex:
(a + b) . (c + d) =
ac + ad + bc + bd
Multiplicação de Monômio
por Polinômio

29. Divisão de Polinômio por
Monômio
Efetuamos a divisão de um polinômio por um
monômio fazendo a divisão de cada termo do
polinômio pelo monômio.
Ex:
(18x3
– 12x2
+ 3x) : (3x) =
= (18x3
: 3x) – (12x2
: 3x) + (3x : 3x)
= 6x2
– 4x + 1

30. Valor Numérico de uma
Após obtida a expressão algébrica, basta substituir
cada incógnita pelo valor estabelecido pelo exercício.
Ex:
3x2
– 2x + 7y + 3x – 17y
3x2
+ x – 10y
Determine o valor numérico da expressão abaixo
para x = 2 e y = 3
1º reduzimos os termos semelhantes
Expressão Algébrica
2º substituímos os valores de x = 2 e y = 3
3.22
+ 2 – 10.3
3.4 + 2 – 30
12 + 2 – 30 = - 16

31. Equações polinomiaisEquações polinomiais
0...2
2
1
10 =++++ −−
n
nnn
axaxaxa
( ) 0=αP
Raízes de uma equaçãoRaízes de uma equação
raizé→α
Teorema da decomposiçãoTeorema da decomposição
( ) n
nnn
axaxaxaxP ++++= −−
...2
2
1
10
( ) ( ) ( ) ( )nrxrxrxaxP −⋅⋅−⋅−⋅= ...210
Polinômios

32. Propriedades:Propriedades:
2) Se b for raiz de P(x) = 0 , então P(x) é divisível por2) Se b for raiz de P(x) = 0 , então P(x) é divisível por
x - b .x - b .
3) Se o número complexo a + bi for raiz de P(x) = 0 ,3) Se o número complexo a + bi for raiz de P(x) = 0 ,
então o conjugado a - bi também será raiz .então o conjugado a - bi também será raiz .
1) Toda equação algébrica de grau n possui exatamente1) Toda equação algébrica de grau n possui exatamente
n raízes .n raízes .
2x2x44
+x³ + 6x² + 2x – 1 = 0+x³ + 6x² + 2x – 1 = 0
Grau da equação ( Representa o número de raízes)Grau da equação ( Representa o número de raízes)
Polinômios

33. 4) Se a equação P(x) = 0 possuir k raízes iguais a m4) Se a equação P(x) = 0 possuir k raízes iguais a m
então dizemos que m é uma raiz de grau deentão dizemos que m é uma raiz de grau de
multiplicidade k .multiplicidade k .
Exemplo: xExemplo: x22
- 8x + 16 = 0, possui duas raízes reais iguais a 4, (x- 8x + 16 = 0, possui duas raízes reais iguais a 4, (x11 = x= x22 = 4).= 4).
Dizemos então que 4 é uma raiz dupla ou de ordem de multiplicidade dois.Dizemos então que 4 é uma raiz dupla ou de ordem de multiplicidade dois.
Propriedades:Propriedades:
Polinômios

34. Lembre que quando:
a.x³ + bx² + cx + da.x³ + bx² + cx + d
= 0= 05) Se a =5) Se a = ±± 11 ∴∴ não há raízes fracionárias.não há raízes fracionárias.
6) Se d = 06) Se d = 0 ∴∴ xx11 = 0 (Lembre a quantidade de= 0 (Lembre a quantidade de
raízes nulas é determinada, pelo menorraízes nulas é determinada, pelo menor
expoente da incógnita.)expoente da incógnita.)
Ex: 2xEx: 2x77
+3x+3x44
+ 2x² = 0+ 2x² = 0
Polinômios

35. Há duas raízes nulas
7) Se a + b + c + d = 07) Se a + b + c + d = 0 ∴∴ xx11 = 1 é raiz.= 1 é raiz.
Polinômios
Lembre que quando:
a.x³ + bx² + cx + da.x³ + bx² + cx + d
= 0= 0
5) Se a =5) Se a = ±± 11 ∴∴ não há raízes fracionárias.não há raízes fracionárias.
6) Se d = 06) Se d = 0 ∴∴ xx11 = 0 (Lembre a quantidade de= 0 (Lembre a quantidade de
raízes nulas é determinada, pelo menorraízes nulas é determinada, pelo menor
expoente da incógnita.)expoente da incógnita.)
Ex: 2xEx: 2x77
+3x+3x44
+ 2x² = 0+ 2x² = 0

36. Toda equação algébrica P(x) = 0 de grau n ≥ 1Toda equação algébrica P(x) = 0 de grau n ≥ 1
admite, pelo menos, uma raiz complexa.admite, pelo menos, uma raiz complexa.
Teorema das raízes complexas ( PRRI)Teorema das raízes complexas ( PRRI)
06²4³ =++− xxx
Polinômios

37. 11 11 ––44 11 66
11 ––33 -2-2 RestoResto ≠≠ 00∴∴x =1 não éx =1 não é
raiz.raiz.
44
Divisores do termo
independente:
±1, ±2, ±3, ±6
-1-1
11 ––55 66 Resto = 0Resto = 0 ∴∴ xx11 = -1 é raiz= -1 é raiz00
Grau n – 1Grau n – 1
0652
=+− xx 22 =x 33 =x
Toda equação algébrica P(x) = 0 de grau n ≥ 1Toda equação algébrica P(x) = 0 de grau n ≥ 1
admite, pelo menos, uma raiz complexa.admite, pelo menos, uma raiz complexa.
Teorema das raízes complexas ( PRRI)Teorema das raízes complexas ( PRRI)
06²4³ =++− xxx
Polinômios

38. Teorema das raízes complexasTeorema das raízes complexas
010144 234
=++−− xxxx 11 −=x
––11 11 ––44 ––11 1414
11 ––55 44 00 RestoResto
Grau n – 2Grau n – 2
01062
=+− xx
1010
12 −=x
1010––11
11 ––66 1010 00 RestoResto
Polinômios

39. 010144 234
=++−− xxxx 11 −=x
01062
=+− xx
12 −=x
acb 42
−=∆
4036 −=∆
4−=∆
a
b
x
2
∆±−
=
2
46 −±
=x
2
26 i
x
±
=
ix ±= 3
ix += 33
ix −= 34
Teorema das raízes complexasTeorema das raízes complexas
Polinômios

40. Teorema das raízes complexas ( PRRF)Teorema das raízes complexas ( PRRF)
18 x3
+ 9x2
- 2x -1 = 0
Polinômios

41. Divisores do
termo
independente:
±1
Teorema das raízes complexas ( PRRF)Teorema das raízes complexas ( PRRF)
18 x3
+ 9x2
- 2x -1 = 0
Polinômios

42. Divisores do coeficiente da incógnita de maior expoente:
±1, ±2, ±3, ±6, ±9, ±18
PRRF:PRRF: ±1/2, ±1/3, ± 1/6, ±1/9, ±1/18
––1/21/2 1818 99 -2-2 -1-1
1818 00 -2-2 00 RestoResto ∴∴ xx11 = -1/2= -1/2
18x² +0x -2 = 0
x² = 1/9
3/12 −=x 3/13 =x
Divisores do
termo
independente:
±1
Teorema das raízes complexas ( PRRF)Teorema das raízes complexas ( PRRF)
18 x3
+ 9x2
- 2x -1 = 0
Polinômios

43. Relações de GirardRelações de Girard
02
=++ cbxax
a
b
xx −=+ 21
a
c
xx =⋅ 21
Polinômios

44. 023
=+++ dcxbxax
a
b
xxx −=++ 321
( ) ( ) ( )
a
c
xxxxxx =⋅+⋅+⋅ 323121
a
d
xxx −=⋅⋅ 321
Relações de GirardRelações de Girard
Polinômios

45. 0...2
2
1
10 =++++ −−
n
nnn
axaxaxa
0
1
321 ...
a
a
xxxx n −=++++
( ) ( ) ( ) ( )
0
2
1413121 ...
a
a
xxxxxxxx nn =⋅++⋅+⋅+⋅ −
( ) ( ) ( )
0
3
12421321 ...
a
a
xxxxxxxxx nnn −=⋅⋅++⋅⋅+⋅⋅ −−
( )
0
321 1...
a
a
xxxx nn
n ⋅−=⋅⋅⋅⋅
Relações de GirardRelações de Girard
Polinômios

46. Teorema do resto (divisor de 1º grau - d = ax + b)Teorema do resto (divisor de 1º grau - d = ax + b)
P(x)P(x) ax + bax + b
Q(x)Q(x)
RR
P(x) = (ax + b)P(x) = (ax + b) · Q(x) + R· Q(x) + R
Raiz do divisorRaiz do divisor
a
b
x −=1
( ) RxQ
a
b
P +⋅=





− 0
R
a
b
P =





−
Polinômios

47. P(x)P(x) ax + bax + b
Q(x)Q(x)
RR
0=R
R
a
b
P =





−
Condição necessária para queCondição necessária para que
P(x) seja divisível por ax + b.P(x) seja divisível por ax + b.
0=





−
a
b
P
Teorema de D’alembertTeorema de D’alembert
Polinômios

48. (UDESC 2006-1) O resto da divisão do polinômio(UDESC 2006-1) O resto da divisão do polinômio
pelo binômiopelo binômio
Teorema do restoTeorema do resto
( ) 111122 23
−+−= xxxxP
( ) 111122 23
−+−= xxxxP ( ) 5−= xxD é:é:
( ) ( ) ( ) ( ) 1511512525
23
−⋅+⋅−⋅=P
( ) 1511251212525 −⋅+⋅−⋅=P
( ) 1553002505 −+−=P
( ) 3013055 −=P
( ) 45 =P
( ) RP =5
Polinômios

49. P(x)P(x) ax + bax + b
Q(x)Q(x)
RR
Grau nGrau n
Grau 1Grau 1
Grau n – 1Grau n – 1
RestoResto
......
......
Coeficientes de P(x)Coeficientes de P(x)
Raiz doRaiz do
divisordivisor
a
b
−
Coeficientes doCoeficientes do
polinômio apolinômio a · Q(x)· Q(x)
RestoResto
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini
Polinômios

50. ( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
22 33 –– 77 66 55
21 =x
33
Polinômios
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

51. 22 33
33
×× ++ ==
––11
–– 77 66 55
Polinômios
( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
21 =x
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

52. 22 33
33
×× ++ ==
––11 44
–– 77 66 55
Polinômios
( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
21 =x
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

53. 22 33
33
×× ++ ==
––11 44 1313
–– 77 66 55
Polinômios
( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
21 =x
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

54. 22 33
33 ––11 44 1313 RestoResto
Coeficientes doCoeficientes do
polinômio apolinômio a · Q(x)· Q(x)
–– 77 66 55
Polinômios
( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
21 =x
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

55. 22 33 –– 77 66 55
33 ––11 44 1313 RestoResto
Coeficientes doCoeficientes do
polinômio apolinômio a · Q(x)· Q(x)
Grau do polinômioGrau do polinômio Q(x) é uma unidadeQ(x) é uma unidade
menor que o grau do polinômio P(x)menor que o grau do polinômio P(x)
( )xQaquociente ⋅→
( ) ( ) 431 2
+−=⋅− xxxQ
( ) 43 2
−+−= xxxQ
13=→ Rresto
Polinômios
( ) 5673 23
++−= xxxxP ( ) 2+−= xxD
21 =x
Dispositivo Briot-RuffiniDispositivo Briot-Ruffini

56. Equações polinomiaisEquações polinomiais
0...2
2
1
10 =++++ −−
n
nnn
axaxaxa
( ) 0=αP
Raízes de uma equaçãoRaízes de uma equação
raizé→α
Teorema da decomposiçãoTeorema da decomposição
( ) n
nnn
axaxaxaxP ++++= −−
...2
2
1
10
( ) ( ) ( ) ( )nrxrxrxaxP −⋅⋅−⋅−⋅= ...210
Polinômios

57. (UDESC 2009 – 2) Seja p um polinômio de grau seis,(UDESC 2009 – 2) Seja p um polinômio de grau seis,
cujos coeficientes de termo de maior grau é igual a 2.cujos coeficientes de termo de maior grau é igual a 2.
As raízes deste polinômio são c, 2 e 0, comAs raízes deste polinômio são c, 2 e 0, com
multiplicidades 3, 2 e 1 respectivamente.multiplicidades 3, 2 e 1 respectivamente.
Considerando p(1) = 16, o valor da raiz c é igual a:Considerando p(1) = 16, o valor da raiz c é igual a:
a) –1.a) –1.
b) .b) .
c) –7.c) –7.
d) 7.d) 7.
e) 15.e) 15.
3
221−
Polinômios

58. (UDESC 2005-1) Sobre todas as raízes da equação(UDESC 2005-1) Sobre todas as raízes da equação
afirma-se que essa equação possui:afirma-se que essa equação possui:04423
=−+− xxx
( ) ( ) 01412
=−⋅+−⋅ xxx
04423
=−+− xxx
( ) ( ) 0142
=−⋅+ xx
042
=+x 01=−x
42
−=x
4−±=x
ix 2±=
1=x
{ }iiS 2,2,1 −=
uma raiz real e duas complexas.uma raiz real e duas complexas.
Polinômios

59. Teorema das raízes complexasTeorema das raízes complexas
010144 234
=++−− xxxx 11 −=x
––11 11 ––44 ––11 1414
11 ––55 44 00 RestoResto
Grau n – 2Grau n – 2
01062
=+− xx
1010
12 −=x
1010––11
11 ––66 1010 00 RestoResto
Polinômios

60. 01062
=+− xx
acb 42
−=∆
4036 −=∆
4−=∆
a
b
x
2
∆±−
=
2
46 −±
=x
2
26 i
x
±
=
ix ±= 3
ix += 33
ix −= 34
Polinômios
Teorema das raízes complexasTeorema das raízes complexas
010144 234
=++−− xxxx 11 −=x
12 −=x

61. (UDESC 2009-1) Seja P(x) um polinômio de terceiro grau,(UDESC 2009-1) Seja P(x) um polinômio de terceiro grau,
cujo gráfico está representado na figura abaixo:cujo gráfico está representado na figura abaixo:
22
2211––11 xx
yy Então o resto da divisão de P(x)Então o resto da divisão de P(x)
pelo monômio x + 2 é:pelo monômio x + 2 é:
Polinômios

62. Professor Antonio Carlos carneiro Barroso
Colégio estadual Dinah Gonçalves
Graduado em Ciências naturais pela UFBA
Pós graduado em Metodologia e Didática
de ensino Superior
Lecionando Matemática e Biologia
http://ensinodematemtica.blogspot.com
Salvador-Ba