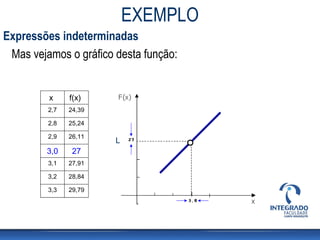
O documento apresenta conceitos sobre cálculo de limites de funções, incluindo regras adicionais para funções racionais e casos de indeterminação. São explicadas propriedades de limites como soma, diferença, produto e quociente. Um exemplo numérico é resolvido usando fatoração para eliminar uma indeterminação.

1. AULA 02
MATEMÁTICA II
Professor: João Alessandro
CÁLCULO DE LIMITES

2. Cálculo - Limites
Para o cálculo do limite de uma função basta substituir o
valor para o qual x está tendendo (valor genérico “a”) na
expressão da função f(x).
No entanto, esta regra falha, algumas vezes (nem
sempre) para funções racionais. Isto acontece quando se
faz a substituição direta de x por seu valor de tendência
e encontra-se indeterminação (0/0 ou b/0 ou ∞/∞ ou ∞/0).
Veja os casos nos slides seguintes.

3. Cálculo - Limites
Regras adicionais
• 1ª Regra: Para funções racionais cujos numeradores e denominadores são 0
quando se substitui x por a (valor de tendência). Neste caso, tanto o
polinômio do numerador quanto o do denominador devem ser divididos por (x
- a). Após esta simplificação, faz-se a substituição de x por a.
x 2 − 4 22 − 4 0
lim = = = Indeterminação
x →2 x − 2 2 −2 0
x2 − 4 ( x − 2)( x + 2)
lim = lim = lim( x + 2) = 2 + 2 = 4
x →2 x − 2 x →2 x −2 x →2

4. Regras adicionais
• 2ª Regra: Quando somente o denominador for 0 na
substituição direta de x, calcula-se os limites laterais.
O limite existirá somente se os limites laterais forem
iguais.
1 1 1
lim = = =
x →2 x − 2 2 − 2 0
1 1
lim = −∞ e lim = +∞.
x −2 x −2
x →2 − x →2 +
Portanto o limite não existe.
Pois pela condição de existência de limite, o limite pela
direita deve ser igual ao limite pela esquerda.

5. Regras adicionais – Limites com e/no Infinito
• 3ª Regra: Quando se tem uma função polinomial ou uma função
racional, os limites destas funções, quando x tende para +∞ ou
-∞, são calculados com base no termo de maior ordem, veja os
exemplos abaixo.
1o exemplo (função racional):
2x3 + x 2 − 5x + 3 2x3
lim = lim = lim 2 x 2 = 2.(∞) 2 = ∞
x →∞ x −2 x →∞ x x →∞
2o exemplo (função polinomial):
lim (5 x 2 − 2 x +1) = lim (5 x 2 ) = 5.(∞) 2 = ∞
x →∞ x →∞

6. EXEMPLO
Expressões indeterminadas:
Considere o seguinte limite:
x − 273
lim
x →3 x − 3
Se fôssemos resolver de acordo com as ferramentas já
conhecidas chegaríamos ao seguinte resultado:
x − 27 3 − 27 0
3 3
lim = =
x →3 x − 3 3−3 0

7. EXEMPLO
Expressões indeterminadas
Mas vejamos o gráfico desta função:
x f(x)
2,7 24,39
2,8 25,24
2,9 26,11
L
3,0 27
3,1 27,91
3,2 28,84
3,3 29,79

8. • Apesar da função não estar definida no ponto x = 3,
quando nos aproximamos de x = 3, f(x) se aproxima
de 27. Portanto:
x − 27
3
lim = 27
x →3 x − 3
• Mas como se resolve a equação algébrica de modo
a chegar a este valor?

9. • Com a FATORAÇÃO de Produtos Notáveis!!!
Neste exemplo, x − 27 = ( x − 3)( x + 3x + 9)
3 2
Logo, podemos reescrever a função do seguinte modo:
( x − 3)( x + 3 x + 9)
2
f ( x) = = x + 3x + 9
2
( x − 3)
Basta então calcular:
lim( x + 3x + 9) = 27
2
x →3

10. FATORAÇÃO
• Diferença de quadrados
a − b = (a + b).(a − b)
2 2
2 2 2 2
(a + b).(a − b) = a − a.b + b.a − b = a − b
Exemplos:
a ) x 2 − 16 = ( x − 4).( x + 4)
b ) 9y 2 − a 2 = (3y + a ).(3y − a )
c ) 16x 4 − 81 =
( 4x 2 − 9).( 4x 2 + 9) = ( 2x − 3).( 2x + 3).( 4x 2 + 9)

11. FATORAÇÃO
• Trinômio quadrado perfeito
(a + b) 2 = (a + b).(a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
(a − b) 2 = (a − b).(a − b) = a 2 − ab − ba + b 2 = a 2 − 2ab + b 2
Exemplos: 2 + 4a + 4 = (a + 2) 2
a
2
16y 6 − 24y 3 + 9 =  4y 3 − 3 
 
 
Não confundir o quadrado da diferença (a - b)2, com a
diferença de quadrados a2 - b2.

12. FATORAÇÃO
• Soma e Diferença de Cubos
a + b = (a + b).(a − ab + b )
3 3 2 2
a − b = (a − b).(a + ab + b )
3 3 2 2
Exemplos:
x + 8 = ( x + 2).( x − x.2 = 2 ) = ( x + 2).( x − 2 x + 4)
3 2 2 2
64a 3 − 125 = (4a)3 − 53 = (4a − 5).(16a 2 = 20a + 25)

13. PROPRIEDADES DE LIMITES
• P1 - O limite da soma é igual a soma dos limites
(caso esses limites existam):
lim[ f ( x) + g ( x)] = lim f ( x) + lim g ( x)
x →a x →a x →a
Exemplo:
lim ( x 2 + 3x + 5) =
x →2
lim x 2 + lim 3x + lim 5 =
x →2 x →2 x →2
lim x 2 + 3 lim x + lim 5
x →2 x →2 x →2
= 2 2 + 3.2 + 5 = 15

14. PROPRIEDADES DE LIMITES
• P2- O limite da diferença é igual a diferença dos
limites (caso esses limites existam):
lim[ f ( x) − g ( x)] = lim f ( x) − lim g ( x)
x→a x→a x→a
Exemplo:
lim(2 x 2 − x) = lim 2 x 2 − lim x
x →2 x →2 x →2
2 lim x − lim x = 2.2 − 2 = 6
2 2
x →2 x →2

15. PROPRIEDADES DE LIMITES
• P3 - O limite do produto é igual ao produto dos limites
(caso esses limites existam):
lim[ f ( x).g ( x)] = lim f ( x). lim g ( x)
x →a x →a x →a
Exemplo:
2
lim( x ) = lim x.x = lim x. lim x = 3.3 = 9
x →3 x →3 x →3 x →3

16. PROPRIEDADES DE LIMITES
• P4- O limite do quociente é igual ao quociente dos limites
(caso esses limites existam):
 f ( x)  lim f ( x )
lim  = x →a
x →a g ( x ) 
  lim g ( x)
x →a
Exemplo:
lim ( x − 5)
 x −5  x →3 3−5 − 2 -1
lim  = = = =
x →3 x 3 − 7 
  lim ( x 3 − 7 ) 27 − 7 20 10
x →3

17. DÚVIDAS?