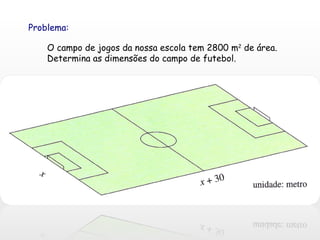
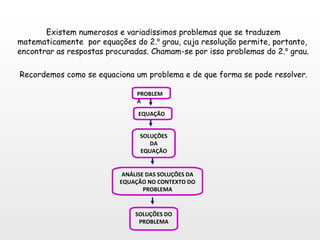
O documento aborda as equações do 2º grau, explicando suas formas canônica, completa e incompleta, e sua resolução através da fórmula de Bhaskara. Ele também discute a relação entre coeficientes e raízes, e como resolver problemas do mundo real utilizando essas equações. Exemplos práticos são fornecidos para ilustrar a aplicação do conteúdo.

1. Equações do 2.º Grau

2. Entre os vários tipos de equações, encontram-se as equações do 2.º grau com uma incógnita, com as quais já tomámos contacto no 8.º ano, mas, apenas em algumas das formas que estas equações podem tomar. O que se pretende neste capítulo é estudar a resolução de qualquer tipo de equações do 2.º grau com uma incógnita, escolhendo a maneira mais adequada de o fazer.

3. Problema: O campo de jogos da nossa escola tem 2800 m 2 de área. Determina as dimensões do campo de futebol.

4. A equação que permite determinar o comprimento e a largura é

5. Temos assim uma equação e neste caso, mais exactamente, uma equação do 2.º grau, já que o maior expoente da incógnita é 2. Chamamos equação do 2.º grau com uma incógnita a toda a expressão que se possa escrever na forma: À forma , chamamos forma canónica . Nota: A maioria das equações do 2.º grau não estão escritas na forma canónica, temos que as colocar utilizando as regras de resolução de equações (parênteses, denominadores,…) Uma equação está escrita na forma canónica quando: - o 1.º membro é um polinómio reduzido; - o 2.º membro é zero.

6. Quando a equação está escrita na forma canónica, dizemos que: é o termo de grau 2 e a o seu coeficiente em x (de grau 1) e b o seu coeficiente independente (de grau zero) é o termo é o termo Assim, e voltando ao nosso problema, temos que é uma equação do 2.º grau, em que:  a= 1 coeficiente do termo de grau 2 ou do 2.º grau;  b=30, coeficiente do termo de grau 1;  c=-2800, coeficiente do termo de grau zero ou termo independente.

7. Exemplos: x 2 - 5x + 6 = 0 , onde a = 1, b = -5 e c = 6. 7x 2 - x = 0 , onde a = 7, b = -1 e c = 0. - x 2 - 36 = 0 , onde a = -1, b = 0 e c = -36. Uma equação do 2º grau é completa quando b e c são diferentes de zero (porque para ser do segundo grau o valor de a tem de ser sempre diferente de zero). A equação que dá resposta ao nosso problema diz-se completa , porque tem os 3 termos (2.º, 1.º e grau 0).

8. Uma equação do 2º grau é incompleta quando b ou c é igual a zero, ou ainda, quando ambos são iguais a zero. Equações da forma ax² +bx = 0, (c = 0) x² - 3x = 0 , onde a = 1, b = -3. -2x² + 4x = 0 , onde a = -2, b = 4. Equações do tipo ax² +c = 0, (b = 0) 3x² - 2 = 0 , onde a = 3, c = -2. x² + 5 = 0 , onde a = 1, c = 5. Equações do tipo ax² = 0, (b=c=0) -2x² = 0 , onde a = -2

9. Raízes de uma Equação do 2º Grau Resolver uma equação do 2º grau significa determinar as suas raízes ou soluções. Raiz ou solução é o número real que, ao substituir a incógnita de uma equação, a transforma numa proposição verdadeira. O conjunto formado pelas raízes de uma equação denomina-se conjunto-solução .

10. Resolução de Equações Incompletas Equações incompletas do tipo Exemplos: De uma forma geral a solução deste tipo de equações é zero.

11. Equações incompletas do tipo Equações da forma: ax² +c = 0, (b = 0) No geral, a equação do tipo ax² +c = 0: possui duas raízes reais simétricas se: - c/a for um nº positivo. Zero, se –c/a=0 não possui raiz real se: - c/a for um nº negativo. Equação possível Equação impossível

12. Exemplos: Se x є R , y є R , x² = y x = √ y ou x = - √ y

13. Equações incompletas do tipo Equações da forma: ax² +bx = 0, (c = 0) A equação do tipo ax² +bx = 0 tem como soluções: x = 0 e x = - b/a

14. Exemplos: Primeiro: Forma canónica; Segundo: Factorização do polinómio; Terceiro: LAP

16. Equações de 2.º grau completas Uma equação do 2º grau é completa quando b e c são diferentes de zero. Denomina-se equação do 2º grau, na incógnita x , toda equação da forma: a x 2 + b x + c=0 ; a ≠ 0. Observa que: a representa o coeficiente de x²; b representa o coeficiente de x; c representa o termo independente. Exemplos: x 2 - 5x + 6 = 0 , onde a = 1, b = -5 e c = 6. 7x 2 – x-10 = 0 , onde a = 7, b = -1 e c =-10. x 2 - 36 = 0 , onde a = 1, b = 0 e c = -36. Incompleta Reparem que nas eq. completas b e c são diferentes de zero.

17. Resolução de Equações Completas Fórmula de Bhaskara Para solucionar equações completas do 2º grau utilizaremos a Fórmula de Bhaskara . A partir da equação ax 2 + bx + c = 0 , a ≠ 0, desenvolveremos passo a passo a dedução da Fórmula de Bhaskara . 1º passo: multiplicaremos ambos os membros por 4a. (4a).(ax² + bx + c) = 0.(4a) 4a²x² + 4abx + 4ac = 0 2º passo: passar 4ac para o 2º membro. 4a²x² + 4abx = - 4ac

18. Fórmula de Bhaskara 3º passo: adicionar b² aos dois membros . 4a²x² + 4abx + b² = b² - 4ac 4º passo: factorizar o 1º membro . (2ax + b) ² = b² - 4ac 5º passo: extrair a raiz quadrada dos dois membros . 6º passo: passar b para o 2º membro .

19. Fórmula de Bhaskara 7º passo: dividir os dois membros por 2a. Assim, a fórmula resolvente da equação do 2º grau:

20. Fórmula resolvente das equações do 2.º grau Em que: a é o coeficiente do termo de grau 2 . b é o coeficiente do termo de grau 1 . c é o coeficiente do termo independente .

21. Nota: S ó se pode aplicar a f ó rmula resolvente quanto uma equa ç ão do 2. º grau est á na forma can ó nica. Exemplo: 1. º Colocar a equa ç ão na forma can ó nica (não est á na forma can ó nica porque o 2. º membro não é zero)

22. Equa ç ões do 2.º grau em que o 1. º membro é o desenvolvimento do quadrado de um bin ó mio Se conseguirmos identificar estes casos, não precisamos de aplicar a fórmula resolvente. Repara: Surgiram duas solu ç ões (ou ra í zes) iguais. Diz-se que -3 é uma solu ç ão ou raiz dupla .

23. Equa ç ões em que o 1. º membro não é o desenvolvimento do quadrado de um bin ó mio, como no primeiro caso que resolvemos, encontram-se as raízes, aplicando a fórmula resolvente. Nota: É possível resolver sempre qualquer equação do 2.º grau , completa ou incompleta , pela fórmula resolvente.

24. Mas, é muito mais simples, resolver aplicando de imediato, a definição da raiz quadrada: É óbvio que:

25. Então: e C.A. 2 56 2 28 2 14 2 7 7 1 Logo:

26. Muito Importante: Ao resolver uma equa ç ão do 2. º grau, deve-se procurar sempre utilizar o processo mais simples: Defini ç ão de raiz quadrada. Lei do anulamento do produto.  F ó rmula resolvente.

27. NÚMERO DE SOLUÇÕES DE UMA EQUAÇÃO DO 2.º GRAU Resolve, utilizando a f ó rmula resolvente, cada uma das seguintes equa ç ões. A equação tem duas raízes diferentes. A equação tem uma raiz dupla ou duas raízes iguais. A equação não tem solução. É impossível em R . S={ } Como não há nenhum número real que elevado ao quadrado dê um número negativo, a ex- pressão não tem significado em R.

28. Uma equação do 2.º grau pode portanto, ter 2 soluções diferentes , 1 solução (ou duas soluções iguais) ou não ter soluções. Observando a resolução destas equações podemos verificar que o número de soluções depende do cálculo da raiz. Sem resolver a equação, como podemos saber o número de raízes? Se pensarmos que na f ó rmula resolvente, , verificamos que a expressão que determina o número de raízes de uma equação, é: À expressão chama-se BINÓMIO DISCRIMINANTE por discriminar o número de soluções de uma equação do 2.º grau. Representa-se por (letra grega que se lê delta).

29. Δ = b 2 - 4ac Podemos agora, escrever a Fórmula de Bhaskara, da seguinte forma: De acordo com o binómio discriminnte, temos três casos a considerar: 1º Caso: Se Δ > 0, a equação tem duas soluções diferentes. 2º Caso: Se Δ = 0, a equação duas soluções iguais, (raiz dupla). 3º Caso: Se Δ < 0, a equação não tem raízes. Equação impossível em R.

30. Δ > O Δ = O Δ < O O valor de √ Δ é real e a equação tem duas raízes reais diferentes , assim representadas: O valor de √ Δ é nulo e a equação tem duas raízes reais e iguais (solução dupla) , assim representadas: O valor de √ Δ não existe em IR , não existindo, portanto, raízes reais. Em R a equação é impossível S= As raízes da equação são número complexos .

31. Se, dada uma determinada equa ç ão, pretendermos saber apenas o n ú mero de solu ç ões (e não necessariamente quais as solu ç ões), basta determinar o bin ó mio discriminante. Δ = b 2 - 4ac

32. Gráfico de uma equação do 2.º grau A representa ç ão gr á fica de uma equa ç ão do 2. º grau é uma curva que se denomina par á bola.

33. Relações entre os Coeficientes e as Raízes 1ª Relação: Soma das Raízes ( S ) Concretamente:

34. 2ª Relação: Produto das Raízes ( P ) Mas como , podemos escrever:

35. Concretamente:

36. Relações entre os Coeficientes e as Raízes Soma das Raízes : É representada pela letra S. S =-b/a Obviamente, se a=1, S=-b Produto das Raízes : É representado pela letra P. P = c/a Se a=1, P=c

37. Composição de uma Equação do 2º Grau, conhecidas as Raízes Considera a equação do 2º grau ax 2 + bx + c = 0. Dividindo todos os termos por a , a ≠ 0, obtemos: Como: S =-b/a e P = c/a, podemos escrever a equação desta maneira: x 2 - Sx + P = 0 Para que serve tudo isto? O conhecimento destas rela ções permite-nos rapidamente escrever uma equa ç ão conhecidas as suas solu ç ões e resolver mentalmente algumas equa ç ões.

38. Exemplos: Somando (S) as duas soluções vem -8 + 5 = -3 Fazendo o produto (P) obtemos Comparemos agora os valores obtidos com a nossa equa ç ão inicial. . S=-b/a P=c/a

39. Vejamos ainda um outro exemplo : CS= {-1, 2} S= 1 P=-2 Neste caso verificamos que, Podemos então concluir: Numa equação do 2.º grau, temos que a soma das soluções é igual a e o produto é igual a .

40. Escreve uma equação do 2.º grau cujas raízes são -2 e 7. A soma das raízes corresponde a: S = -2 + 7 = 5 O produto das raízes corresponde a: P = -2 . 7 = -14 A equação é dada por x 2 - Sx + P = 0 , onde S = 5 e P = -14. Logo, x 2 - 5x - 14 = 0 é a equação procurada. Exercício:

41. Escreve uma equação cuja: Exercício: a) solu ç ão seja 5 e 10. S = 15 P = 50 Então, ) solução seja e -6. S = -11/2 P = -3 Então:

42. Resolve mentalmente a equa ç ão S = 0 P = - 9/4 É necess á rio descobrir dois n ú meros cujo produto dê -9/4 e a soma dê 0. Assim: S = Exercício:

43. Resolu ç ão de problemas que envolvem equa ç ões do 2. º grau.

44. Existem numerosos e variad í ssimos problemas que se traduzem matematicamente por equa ç ões do 2. º grau, cuja resolu ç ão permite, portanto, encontrar as respostas procuradas. Chamam-se por isso problemas do 2. º grau. Recordemos como se equaciona um problema e de que forma se pode resolver. PROBLEMA EQUAÇÃO SOLUÇÕES DA EQUAÇÃO ANÁLISE DAS SOLUÇÕES DA EQUAÇÃO NO CONTEXTO DO PROBLEMA SOLUÇÕES DO PROBLEMA

45. A Rita é três anos mais nova que a sua irmã e o produto das suas idades é 18. Quantos anos tem a Rita? Exemplo 1 Resolução: Traduzindo em linguagem matemática, vem: Idade da Rita- Idade da irmã da Rita- ou Idade da Rita- Idade da irmã da Rita- Equacionando o problema e resolvendo a equação: A equação tem duas soluções, mas apenas uma é solução do problema, atendendo que a idade da Rita só pode ser 3. R.: A Rita tem 3 anos e a irmã tem 6 anos.

46. Exemplo 2 De um campo de voleibol sabemos que o seu perímetro mede 27 metros e a sua área mede 40,5 metros quadrados. Quais são as dimensões do campo? Resolução: Traduzindo para linguagem matemática, vem: Largura- Comprimento: y Perímetro: Área: R.: As dimensões do camp o de voleibol são 4,5 por 9 metros.

47. Problema do caderno de actividades página 80. 23. A figura representa a trajectória de um foguete que o Jorge lançou no arraial de S. João. 23.1 Qual foi a altura máxima atingida pelo foguete? 23.2 A que altura se encontrava o foguete decorridos 2 segundos? E 10 segundos? 23.4 Onde se encontrava o foguete nos instantes t=0 e t=12? 23.5 Sabendo que a atura atingida pelo foguete é dada pela expressão , confirma, analiticamente, o momento de chegada ao solo. 23.3 Qual o valor de h(0)? Explica o significado da afirmação: «h(t)=0 quando t=0.»

48. 30. Num referencial ortonormado xOy, está representada parte do gráfico da função: No mesmo referencial está também representado um triângulo [ABC], cujos vértices pertencem ao gráfico da função f. Determina a área do triângulo [ABC].

49. 9. Um campeão de saltos de trampolim, decide preparar uma série de saltos para uma competição. A figura mostra um desses saltos cuja trajectória é dada pela expressão (h em metros e t em segundos). 9.1 Determina a altura do topo da prancha até ao solo. 9.2 Determina o instante em que o campeão penetra na água. 9.3 A que altura do solo está o atleta ao fim de 2 segundos?

50. 32. A Rita saiu de casa para visitar a avó. A distância d, em quilómetros, que a Rita tem de percorrer para chegar à casa da avó, t horas após ter iniciado a caminhada é dada pela expressão: Numa pequena composição, explica os seguintes aspectos: a distância que a Rita percorreu até chegar á casa da avó; O tempo que demorou a chegar à casa da avó; O valor de d(1), indicando o seu significado no contexto do problema.

51. 31. Um fio encontra-se suspenso entre dois postes. A distância entre ambos é de 18 metros. Considera a função f definida por: Admite que f(x) é a distância do solo, em metros, do ponto do fio situado a y metros à direita do 1.º poste. 31.1 Mostra que a altura do 1.º poste é 5 metros e a altura do 2.º poste é 14 metros. 31.2 Calcula o valor de y, sabendo que o ponto do fio correspondente está à mesma altura do solo que o primeiro poste.