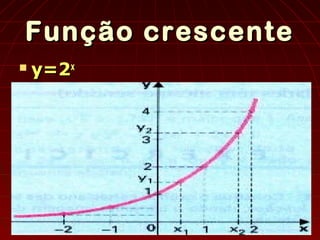
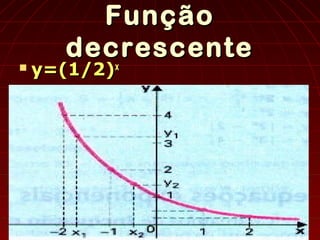
O documento define funções exponenciais como aquelas onde a variável aparece em expoente. A função f(x)=ax, com a>0 e a≠1, é chamada de função exponencial de base a. O documento descreve as características gráficas dessas funções, como o domínio, contradomínio e forma da curva, e apresenta exemplos de resolução de equações e inequações exponenciais.

1. Função
Exponencial
Prof. Gledson Guimarães

2. Definição

Chamamos de
funções
exponenciais
aquelas nas
quais temos a
variável
aparecendo
em expoente.

A função f:IRIR+
definida por
f(x)=ax, com a ∈
IR+ e a≠1, é
chamada função
exponencial de
base a .

3. Domínio e
Contradomínio
 O domínio dessa função é
o conjunto IR (reais) e o
contradomínio é IR+
(reais positivos, maiores
que zero).

4. GRÁFICO CARTESIANO
DA EXPONENCIAL
Temos 2 casos a considerar:
 quando a>1;
Exemplo: y=2x (nesse caso, a=2, logo
a>1)
 quando 0<a<1.
Exemplo: y=(1/2)x (nesse caso, a=1/2,
logo 0<a<1)


5. Função crescente

y=2x

6. 
Função
decrescente
y=(1/2)x

7. Características Gráficas



o gráfico nunca intercepta o
eixo horizontal; a função não
tem raízes;
o gráfico corta o eixo vertical
no ponto (0,1);
os valores de y são sempre
positivos, portanto o
conjunto imagem é Im=IR+.

8. EQUAÇÕES
EXPONENCIAIS


Para resolver equações exponenciais,
devemos realizar dois passos
importantes:
1º) redução dos dois membros da
equação a potências de mesma
base;
2º) aplicação da propriedade :
m
n

a = a ⇒ m = n (a ≠ 1 e a > 0 )

9. 



Exemplos de
equações
x
3 =81 (x=4)
x
9 = 1
3x-1
2x
2 = 32
2x
x
3 –6.3 –27=0

10. Resoluções

3 =81
x
81=3 logo 3 = 3
x=4
S = {4}
4
x
4

11. Resoluções

9 = 1
x
9 = 1 ⇒ 9 = 9 ; logo
x=0.
S = {0}
x
x
0

12. Resoluções

2 = 32
3x-1
2x
2 = 32
2 3x-1 = (2 5 ) 2x
3x-1
10x
2 =2
3x-1=10x
x=-1/7
3x-1
2x
S = {-1/7 }

13. Resoluções

3 –6.3 –27=0
2x
x
32x–6.3x–27=0
(3x)2-6.3x–27=0
Fazendo 3x=y,
y2-6y–27=0
aplicando Bhaskara encontramos
-3 e y’’= 9
y’=
Para achar o x, devemos voltar os valores
para a equação auxiliar 3x = y:
y’= -3 ⇒ 3x’ = -3 ⇒ não existe x’, pois
potência de base positiva é positiva
y’’= 9 ⇒ 3x’’ = 9 ⇒ 3x’’ = 32 ⇒ x’’=2

14. Inequações
Exponenciais



A resolução de inequações
exponenciais tem dois passos
importantes:
1º) redução dos dois membros da
inequação a potências de mesma
base;
2º) aplicação da propriedade:

15. Inequações
Exponenciais

a>1
am > an ⇒ m>n
(as desigualdades têm mesmo
sentido)

0<a<1
am > an ⇒ m<n
(as desigualdades têm sentidos ≠)

16. Exemplo
1 ) 4 x −1 + 4 x − 4 x +1 >
− 11
4
Resolução :
4x
− 11
x
x
A inequação pode ser escrita
+ 4 − 4 .4 >
.
4
4
Multiplicando ambos os lados por 4 temos :
4 x + 4.4 x − 16.4 x > −11 , ou seja :
( 1 + 4 − 16 ).4 x > −11 ⇒ -11.4 x > −11 e daí, 4 x < 1
Porém, 4 x < 1 ⇒ 4 x < 4 0 .
Como a base (4) é maior que 1, obtemos :
4 x < 40 ⇒ x < 0
Portanto S = IR - (reais negativos)