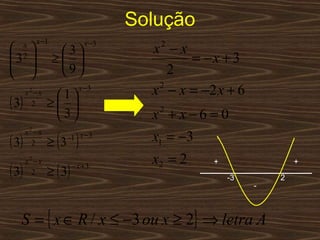
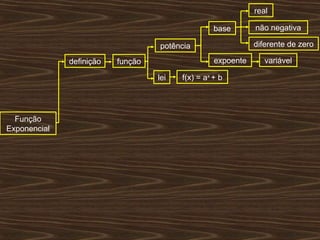
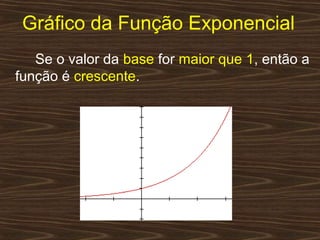
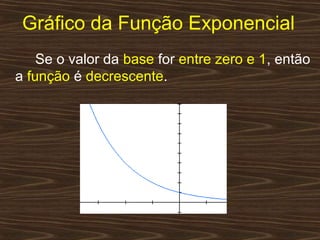
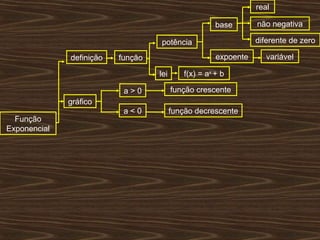
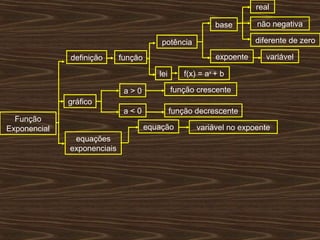
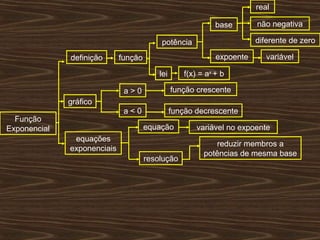
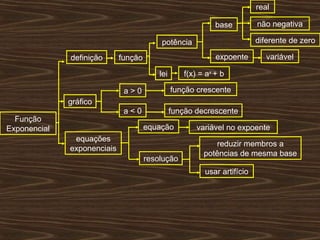
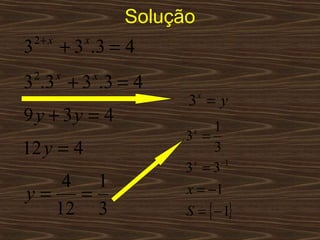
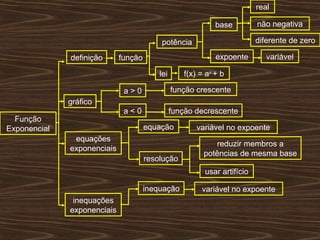
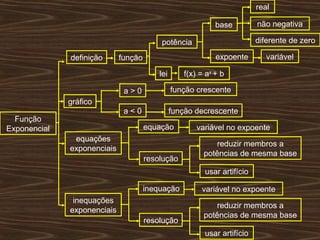
O documento aborda funções exponenciais, definindo-as como funções onde a variável está no expoente e apresentando exemplos e gráficos que demonstram seu comportamento crescente ou decrescente dependendo da base. Além disso, discute como resolver equações e inequações exponenciais. Por fim, menciona a bibliografia utilizada para a elaboração do conteúdo.

1. Função
Exponencial

2. Para aproveitar 100% dessa aula
você precisa saber:
• Potenciação e Radiciação
• Introdução às Funções
• Função Afim
• Função quadrática
• Inequações do 1º e do 2º graus

3. O que você
sabe sobre
Função
exponencial?

4. Função exponencial
É toda função na qual a variável aparece no
expoente. É definida por uma lei na forma
f(x) = ax + b, sendo a um número real, não-
negativo e diferente de 1.
Exemplos:  f(x) = 5x
 y = (1,2)x
2
 g(x) = ( )x + 1

5. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
Função
Exponencial

6. Gráfico da Função Exponencial
Se o valor da base for maior que 1, então a
função é crescente.

7. Gráfico da Função Exponencial
Se o valor da base for entre zero e 1, então
a função é decrescente.

8. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial

9. Exercício
Para quais valores reais de m a função
y = (3m - 2)x é decrescente?

10. Exercício
Para quais valores reais de m a função
y = (3m - 2)x é decrescente?

11. Solução
decrescente ⇒ a > 0 e a < 1
3m − 2 > 0 3m − 2 < 1
3m > 2 3m < 3
2 m <1
m>
3
2
Re sposta : < m < 1
3

12. Equações exponenciais
É a equação onde a variável aparece no
expoente.
Exemplos:
a )4 = 32
x
x
1
b)  = 81
3
x +1
c)25 = 5 x
d )2 2x
= 2 + 12
x

13. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial equação variável no expoente
equações
exponenciais

14. Como resolvemos uma
Equação Exponencial?
Basta reduzir os dois membros da equação
a potências de mesma base.
Exemplos:
x −1
A) 3 = 81
x −1
3 =3 4
x −1 = 4
x = 5 ⇒ S = { 5}

15. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial equação variável no expoente
equações
reduzir membros a
exponenciais
potências de mesma base
resolução

16. x
1 3
B)   = 4 C) 0,75 =
x 9
2 16
(2 )
x
−1 x
= 2
3 2  75  9
  =
2
 100  16
−x
2 =2 3 x
3 9
2   =
−x= 4 16
3 x 2
3 3
2   = 
x=− 4 4
3
x=2
 2
S = −  S = { 2}
 3

17. x 2 −5 x + 6
D) 0,1 = 1000
x
E) 11 =1
x x 2 −5 x + 6
1 11 = 11 0
  = 1000
 10  x − 5x + 6 = 0
2
(10 )−1 x
= 10 3
x1 = 2
10 −x
= 10 3
x2 = 3
−x=3 S = { 2,3}
x = −3
S = { − 3}

18. Tente fazer sozinho!
Resolva a equação:
2 x +1 3 x +1 x −1
2 .4 =8

19. Solução
2 x +1 3 x +1 x −1
2 .4 =8
2 2 x +1
.2 ( )
2 3 x +1
( )
= 2 3 x −1
2 x +1 6 x+2 3 x −3
2 .2 =2
8 x +3 3 x −3
2 =2
8 x + 3 = 3x − 3
5 x = −6
6  6
x = − ⇒ S = − 
5  5

20. E se não puder reduzir
os dois membros da
equação a potências
de mesma base?

21. Vamos usar
um artifício!!!

22. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial equação variável no expoente
equações
reduzir membros a
exponenciais
potências de mesma base
resolução
usar artifício

23. A) x+2 x −1
2 − 3.2 = 20
2 x .2 2 − 3.2 x .2 −1 = 20
2 =y
x
1
y.4 − 3. y. = 20
2 2 =8
x
3y
4y − = 20 2 =2
x 3
2
x=3
8 y − 3 y = 40
S = { 3}
5 y = 40
y =8

24. Tente fazer sozinho!
Resolva a equação:
2+ x
3 + 3 .3 = 4
x

25. Solução
2+ x
3 + 3 .3 = 4
x
3 .3 + 3 .3 = 4
2 x x
3 =yx
9 y + 3y = 4
1
3 =
x
12 y = 4 3
3 x = 3−1
4 1 x = −1
y= =
12 3 S = { − 1}

26. Inequações exponenciais
É a inequação onde a variável aparece
no expoente.
Exemplos: a ) 4 x ≥ 128
x
1
b)  < 27
3
x +1
c)25 ≤ 5 x
d )2 2x
> 2 + 12
x

27. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial equação variável no expoente
equações
reduzir membros a
exponenciais
potências de mesma base
resolução
usar artifício
inequação variável no expoente
inequações
exponenciais

28. Como resolvemos uma
Inequação Exponencial?
Usando as mesmas
regras com as quais
resolvemos uma equação.

29. real
base não negativa
potência diferente de zero
definição função expoente variável
lei f(x) = ax + b
a>0 função crescente
gráfico
a<0 função decrescente
Função
Exponencial equação variável no expoente
equações
reduzir membros a
exponenciais
potências de mesma base
resolução
usar artifício
inequação variável no expoente
inequações
reduzir membros a
exponenciais
potências de mesma base
resolução
usar artifício

30. x +1
A) 25 ≤ 5 x
B) 2 2 x < 2 x + 12
(5 )
2 x +1
≤5
x
2 (2 )
x 2
< 2 + 12
x
2 =y
x
x y 2 < y + 12
52 x + 2 ≤ 5 2
2 <4
x
y − y − 12 < 0
2
x 2 <2
x 2
2x + 2 ≤ y 2 − y − 12 = 0
2 x<2
4x + 2 ≤ x y1 = −3
S = ] − ∞,2[
3x ≤ 2 y2 = 4
2  2
x ≤ ⇒ S =  − ∞, 
3  3

31. Tente fazer sozinho!
(Vunesp - SP) É dada a inequação
x −1 x −3
  3
x
3  ≥   2
  9
 
O conjunto verdade, considerando o conjunto
universo como sendo o dos reais, é dado por:
a)V = { x ∈ R / x ≤ − 3 ou x ≥ 2}
b)V = { x ∈ R / x ≤ − 3 e x ≥ 2}
c)V = { x ∈ R / − 3 ≤ x ≤ 2}
d )V = { x ∈ R / x ≤ − 3}
e)V = { x ∈ R / x ≥ 2}

32. Tente fazer sozinho!
(Vunesp - SP) É dada a inequação
x −1 x −3
  3
x
3  ≥   2
  9
 
O conjunto verdade, considerando o conjunto
universo como sendo o dos reais, é dado por:
a)V = { x ∈ R / x ≤ − 3 ou x ≥ 2}
b)V = { x ∈ R / x ≤ − 3 e x ≥ 2}
c)V = { x ∈ R / − 3 ≤ x ≤ 2}
d )V = { x ∈ R / x ≤ − 3}
e)V = { x ∈ R / x ≥ 2}

33. Solução
x −1 x −3
 x
 3 x2 − x
3

2 
 ≥  = −x + 3
  9 2
x2 − x
1
x −3
x − x = −2 x + 6
2
( 3) 2 ≥ 
3 x2 + x − 6 = 0
( )
x2 − x
( 3) 2 ≥ 3 −1 x −3 x1 = −3
x2 − x x2 = 2 + +
( 3) 2 ≥ ( 3)
− x +3
-3 2
-
S = { x ∈ R / x ≤ −3 ou x ≥ 2} ⇒ letra A

34. O que vimos nessa aula:
• O que é função exponencial
• Como é o gráfico da função exponencial
• Como resolver equações exponenciais
(com e sem artifício)
• Como resolver inequações exponenciais.

35. Bibliografia
• Dante, Luiz Roberto – Matemática Contexto
e Aplicações. 4ª edição – 2008. Editora
Ática – SP. Páginas: 194 a 223.
• Iezzi, Gelson; Dolce, Osvaldo; Périgo,
Roberto; Degenszajn, David – Matemática
(volume único). 4ª edição – 2007. Editora
Atual – SP. Páginas: 86 a 102.
• Bianchini, Edwaldo; Paccola, Herval –
Curso de Matemática. 3ª edição – 2003.
Editora Moderna – SP. Páginas: 123 a 131.