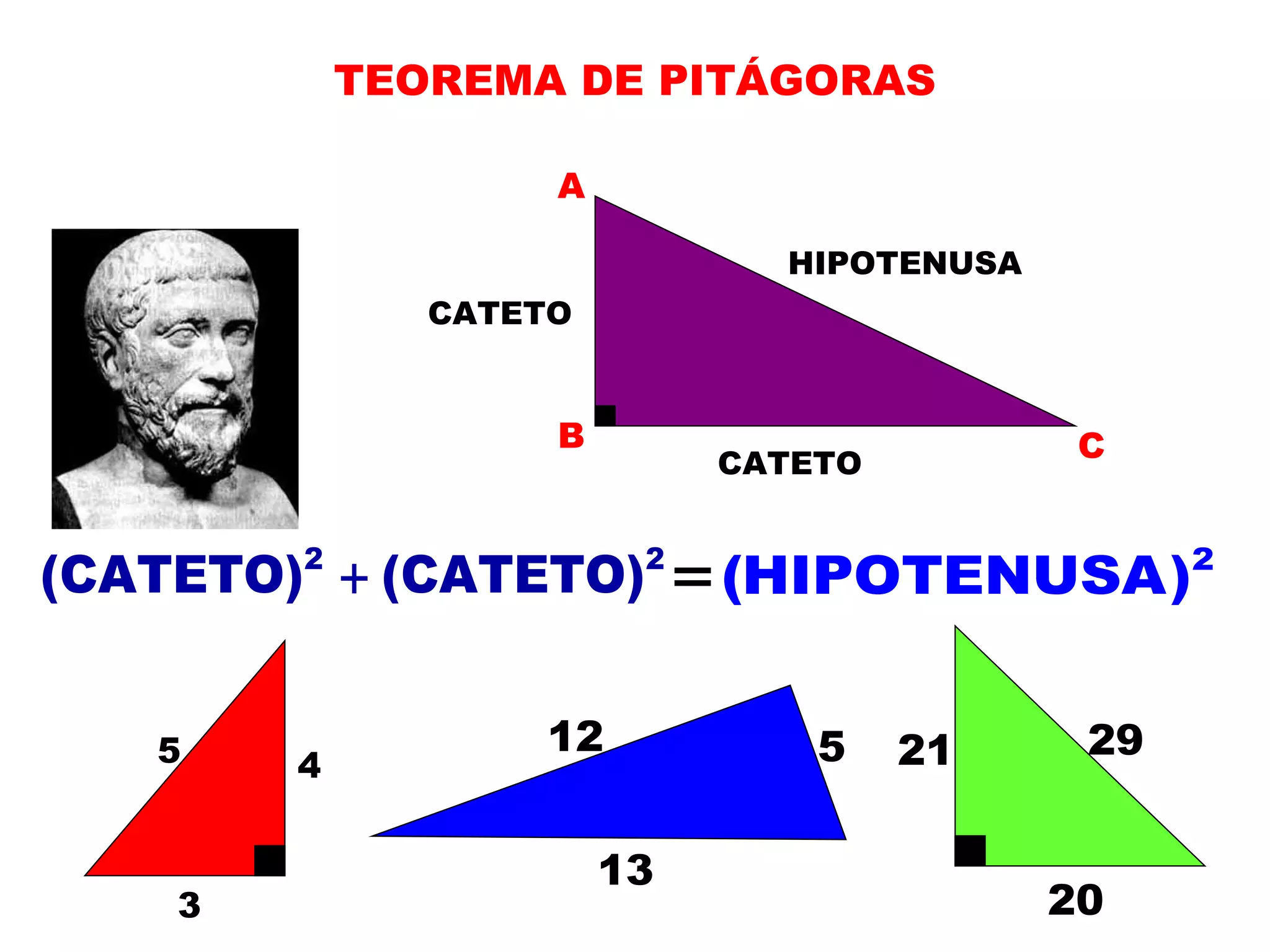
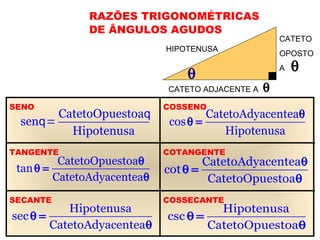
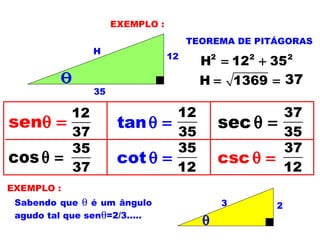
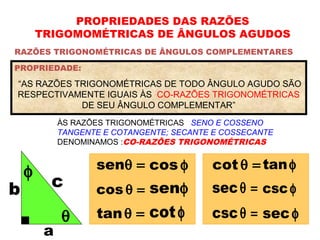
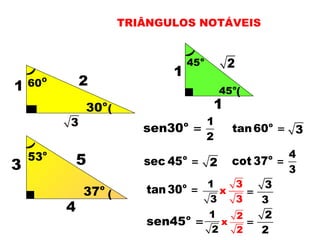
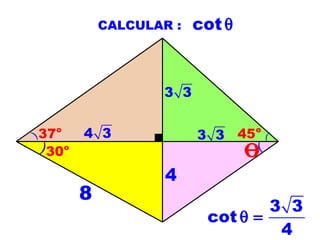
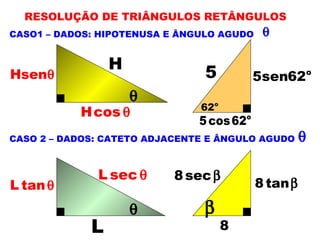
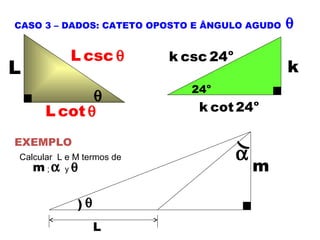
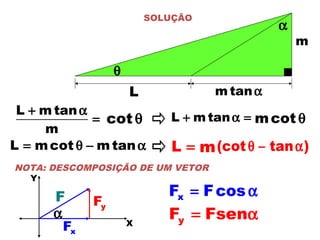
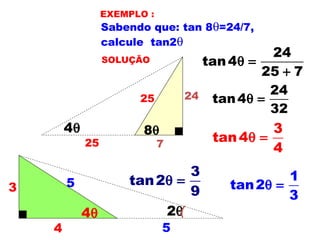
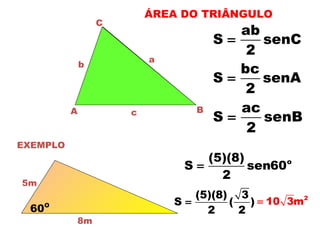
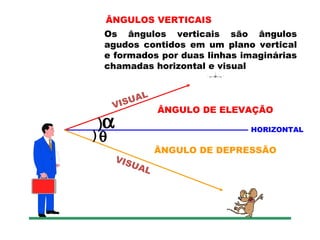
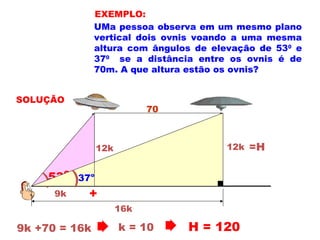
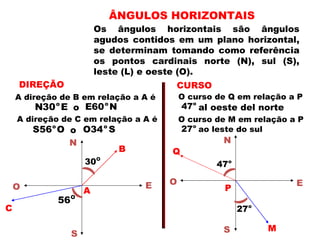
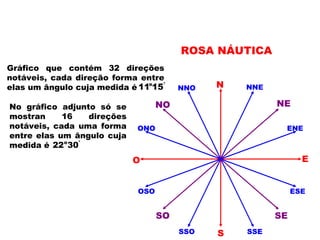
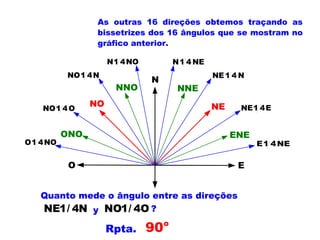
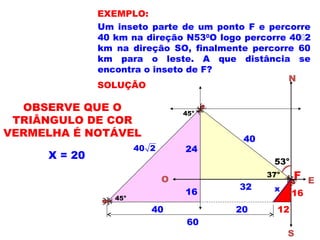
1) O documento apresenta os conceitos fundamentais de trigonometria, incluindo o Teorema de Pitágoras, razões trigonométricas, propriedades e exemplos de resolução de triângulos retângulos e notáveis. 2) É explicado o cálculo de áreas de triângulos e a resolução de problemas envolvendo ângulos verticais e horizontais. 3) Por fim, são apresentados exemplos numéricos ilustrando os conceitos e propriedades trigonométricas.

1. TEOREMA DE PITÁGORAS
A
B C
CATETO
CATETO
HIPOTENUSA
2 2
(CATETO) (CATETO)+ = 2
(HIPOTENUSA)
3
45 512
13
20
21 29

2. RAZÕES TRIGONOMÉTRICAS
DE ÂNGULOS AGUDOS
q
=q
CatetoOpuestoa
sen
Hipotenusa
θ
θ =
CatetoAdyacentea
cos
Hipotenusa
θ =
θ
Hipotenusa
sec
CatetoAdyacentea
θ =
θ
Hipotenusa
csc
CatetoOpuestoa
θ
θ =
θ
CatetoAdyacentea
cot
CatetoOpuestoa
θ
θ =
θ
CatetoOpuestoa
tan
CatetoAdyacentea
CATETO
OPOSTO
A
θCATETO ADJACENTE A
θ
HIPOTENUSA
θ
SENO COSSENO
TANGENTE COTANGENTE
SECANTE COSSECANTE

3. 12
35
H
2 2 2
H 12 35= +
TEOREMA DE PITÁGORAS
H 1369= = 37
senθ =
cosθ =
tanθ =
12
37
35
37
12
35
cot θ =
sec θ =
csc θ =
35
12
37
35
37
12
EXEMPLO :
EXEMPLO :
Sabendo que θ é um ângulo
agudo tal que senθ=2/3.....
23
θ
θ

4. RAZÕES TRIGONOMÉTRICAS RECÍPROCAS
PROPRIEDADES DAS RAZÕES
TRIGOMOMÉTRICAS DE
ÂNGULOS AGUDOS
1
sen
csc
θ =
θ
1
cos
sec
θ =
θ
1
tan
cot
θ =
θ
EXEMPLOS
o
1
A)
sen36
o
csc 36= o
1
B)
cos17
o
sec17=
sen csc 1θ θ = cos sec 1θ θ = tan cot 1θ θ =
D)sen2 csc2θ θ 1=o o
C)tan49 cot 49 1=
o
E)cos63 sec θ 1= o
63θ =
F)tan2 cot 1φ θ = 2φ = θ

5. PROPRIEDADES DAS RAZÕES
TRIGOMOMÉTRICAS DE ÂNGULOS AGUDOS
RAZÕES TRIGONOMÉTRICAS DE ÂNGULOS COMPLEMENTARES
ÀS RAZÕES TRIGONOMÉTRICAS SENO E COSSENO
TANGENTE E COTANGENTE; SECANTE E COSSECANTE
DENOMINAMOS :CO-RAZÕES TRIGONOMÉTRICAS
PROPRIEDADE:
“AS RAZÕES TRIGONOMÉTRICAS DE TODO ÂNGULO AGUDO SÃO
RESPECTIVAMENTE IGUAIS ÀS CO-RAZÕES TRIGONOMÉTRICAS
DE SEU ÂNGULO COMPLEMENTAR”
θ
φ senθ = cos φ
cos θ =
tanθ =
senφ
cotφ
a
b c
cot θ =
secθ =
cscθ =
tanφ
cscφ
sec φ

6. EXEMPLOS
o
A)sen25 =
o
B)tan43 =
o
C)sec60 =
o
cos65
o
cot 47
o
csc30
...............
...............
...............
o o O
25 65 90+ =
o o O
43 47 90+ =
o o O
60 30 90+ =
o
D)sen cos20θ =
o O
20 90θ + = o
70θ =
E)tan5 cotα = α
o
5 90α + α =
o
15α =
F)sen
5
π  = ÷
 
cos θ
5 2
π π
θ + =
2 5
π π
θ = −
3
rad
10
π
θ =

7. TRIÂNGULOS NOTÁVEIS
1 2
3
o
30 (
)
O
60
1
1
2
o
45
o
45
(
)
3
4
5
o
37
o
53
(
)
o
sen30 =
1
2
o
tan60 = 3
o
sec 45 = 2
o
cot 37 =
4
3
o
tan30 =
1
3
3
x
3
3
3
=
o
sen45 =
1
2
2
x
2
2
2
=

8. )
)
(
(o
30
o
37 o
45
θ
4 3
4
3 3
3 3
CALCULAR : cotθ
8
3 3
cot
4
θ =

9. RESOLUÇÃO DE TRIÂNGULOS RETÂNGULOS
θ
θ
H
Hsenθ
Hcos θ
L sec θ
L tanθ
L
5
o
62
o
5sen62
o
5cos62
8
β
8 tanβ
8secβ
CASO1 – DADOS: HIPOTENUSA E ÂNGULO AGUDO θ
CASO 2 – DADOS: CATETO ADJACENTE E ÂNGULO AGUDO θ

10. L
θ
L cot θ
L csc θ
k
o
24
o
k csc 24
o
k cot 24
EXEMPLO
α
θ)
)
m
Calcular L e M termos de
m α y θ;
L
CASO 3 – DADOS: CATETO OPOSTO E ÂNGULO AGUDO θ

11. SOLUÇÃO
α
θ
m
m tanαL
L m tan
m
+ α
= cot θ L m tan+ α = mcot θ
L mcot m tan= θ − α L = m(cot tan )θ − α
NOTA: DESCOMPOSIÇÃO DE UM VETOR
α
F
yF
xF X
Y
xF Fcos= α
yF Fsen= α

12. ÁREA DO TRIÂNGULO
A B
C
a
b
c
ab
S senC
2
=
bc
S senA
2
=
ac
S senB
2
=
EXEMPLO
5m
8m
O
60
o(5)(8)
S sen60
2
=
(5)(8) 3
S ( )
2 2
= 2
10 3m=

13. ÂNGULOS VERTICAIS
Os ângulos verticais são ângulos
agudos contidos em um plano vertical
e formados por duas linhas imaginárias
chamadas horizontal e visual
α
θ
ÂNGULO DE ELEVAÇÃO
ÂNGULO DE DEPRESSÃO
HORIZONTAL
VISUAL
VISUAL
)
)

14. UMa pessoa observa em um mesmo plano
vertical dois ovnis voando a uma mesma
altura com ângulos de elevação de 530
e
370
se a distância entre os ovnis é de
70m. A que altura estão os ovnis?
EXEMPLO:
SOLUÇÃO
) ) o
37
O
53
70
12k 12k
)
O
53
9k
) o
37
16k
+
9k +70 = 16k k = 10 H = 120
=H

15. ÂNGULOS HORIZONTAIS
Os ângulos horizontais são ângulos
agudos contidos em um plano horizontal,
se determinam tomando como referência
os pontos cardinais norte (N), sul (S),
leste (L) e oeste (O).
DIREÇÃO
A direção de B em relação a A é
E30N o
N60E o
A direção de C em relação a A é
o
S56 O S34O o
o
o
CURSO
O curso de Q em relação a P
o
47
O curso de M em relação a P
o
27 ao leste do sul
al oeste del norte
N
S
EO
O
30
O
56
A
B
C
EO
S
N
P
Q
o
47
o
27
M
)
(
(
)

16. ROSA NÁUTICA
Gráfico que contém 32 direções
notáveis, cada direção forma entre
elas um ângulo cuja medida é
'o
1511
No gráfico adjunto só se
mostran 16 direções
notáveis, cada uma forma
entre elas um ângulo cuja
medida é 'o
3022
N
S
EO
NNE
ENE
NNO
ONO
OSO
SSO
ESE
SSE
NENO
SO SE

17. As outras 16 direções obtemos traçando as
bissetrizes dos 16 ângulos que se mostram no
gráfico anterior.
E
NE
N
NNE
ENE
NE41E
E41NE
NE41N
N41NE
NNO
NO41N
N41NO
NOO41NO
ONO
NO41O
O
Quanto mede o ângulo entre as direções
NE1/ 4N y NO1/ 4O ?
Rpta.
o
90

18. Um inseto parte de um ponto F e percorre
40 km na direção N530
O logo percorre 402
km na direção SO, finalmente percorre 60
km para o leste. A que distância se
encontra o inseto de F?
EXEMPLO:
SOLUÇÃO
N
S
EO
o
53
)
o
45
o
45
40
40 2
60
x
o
37
24
32
16
40 20 12
16
OBSERVE QUE O
TRIÂNGULO DE COR
VERMELHA É NOTÁVEL
X = 20
F

19. EXEMPLO :
Sabendo que: tan 8θ=24/7,
calcule tan2θ
SOLUÇÃO
8θ
24
7
25
4θ
25
24
tan4
25 7
θ =
+
24
tan4
32
θ =
3
tan4
4
θ =
4θ 2θ
3
4
5
5
3
tan2
9
θ = 1
tan2
3
θ =
(

20. Professor Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
Graduado em Ciências Naturais pela UFBA
Pós graduado em Metodologia e Didática de ensino
Superior
Lecionando Matemática e Biologia
http://ensinodematemtica.blogspot.com
www.profantoniocarneiro.com
Salvador-Ba