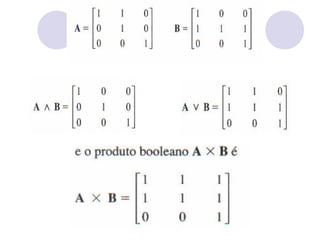
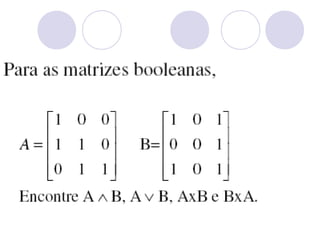
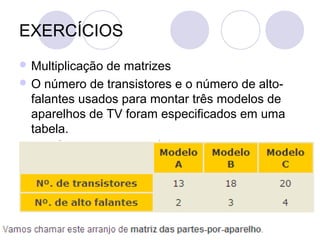
O documento apresenta as informações biográficas de um professor de matemática e biologia, incluindo sua formação acadêmica e experiência de ensino. Em seguida, define e explica conceitos básicos sobre matrizes, como dimensões, elementos, transposição, adição, subtração e multiplicação de matrizes.

1. Professor Antonio Carlos carneiro
Barroso
Colégio Estadual Dinah Gonçalves
Graduado em Ciências naturais pela UFBA
Pós graduado em Metodologia e Didática de ensino
Superior
Lecionando Matemática e Biologia
http://ensinodematemtica.blogspot.com
Salvador-Ba
2012

2. Matrizes

3. Matriz

4. As linhas horizontais da matriz são
chamadas de linhas e as linhas verticais
são chamadas de colunas.
Uma matriz com m linhas e n colunas é
chamada de uma matriz m por n (escreve-
se m×n) e m e n são chamadas de suas
dimensões, tipo ou ordem.

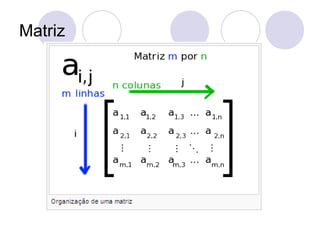
5. Um elemento de uma matriz A que está
na i-ésima linha e na j-ésima coluna é
chamado de elemento i,j ou (i,j)-ésimo
elemento de A.
Ele é escrito como Ai,j ou A[i,j].

6. Matriz
Uma matriz onde uma de suas dimensões
é igual a 1 é geralmente chamada de
vetor.
Uma matriz 1 × n (uma linha e n colunas)
é chamada de vetor linha ou matriz
linha, e uma matriz m × 1(uma coluna e
m linhas) é chamada de vetor coluna ou
matriz coluna.

7. A matriz a seguir é uma matriz de ordem 2×3
com elementos naturais
Nesse exemplo, o
elemento a1 2 é 2, o número
na primeira linha e
segunda coluna do quadro.

14. Transposta
A transposta de uma matriz Am × n é a
matriz At
n × m em que , ou seja, todos os
elementos da primeira linha, tornar-se-ão
elementos da primeira coluna, todos os
elementos da segunda linha, tornar-se-ão
elementos da segunda coluna, todos os
elementos da n linha, tornar-se-ão
elementos da m coluna.

15. Exemplos:

16. Matriz Quadrada
Uma matriz é dita quadrada se tem o
mesmo número de linhas e colunas, ou
seja, quando podemos dizer que, m tem a
mesma quantidade de elementos que n.
Numa matriz quadrada A de ordem n × n,
chama-se de diagonal principal os
elementos aij onde i = j, para i de 1 a n.

17. http://ensinodematemtica.blogspot.com

18. Diagonal

19. Operações envolvendo Matrizes
Multiplicação por um escalar
A multiplicação é uma das operações mais
simples que podem ser feitas com
matrizes.
Para multiplicar um número k qualquer por
uma matriz n×m A, basta multiplicar cada
entrada aij de A por k.
Assim, a matriz resultante B será também
n×m e bij = k.aij.

20. Operações envolvendo Matrizes
 Com isso, pode-se pensar também na noção de
dividir uma matriz por um número: basta
multiplicá-la pelo inverso desse número.
 Mas essa noção pode ser perigosa: enquanto a
multiplicação entre um número e uma matriz
pode ser dita "comutativa", o mesmo não vale
para a divisão, pois não se pode dividir um
número por uma matriz.

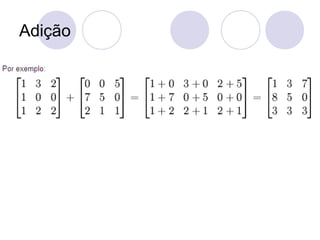
22. Adição e Subtração entre Matrizes
Dado as matrizes A e B do tipo m por n,
sua soma A + B é a matriz m por n
computada adicionando os elementos
correspondentes: (A + B)[i,j] = A[i, j] +
B[i,j].

23. Adição

25. Nota

26. Subtração

27. Multiplicação de Matrizes
Multiplicação de duas matrizes é bem
definida apenas se o número de colunas
da matriz da esquerda é o mesmo número
de linhas da matriz da direita.
Se A é uma matriz m por n e B é uma
matriz n por p, então seu produto AB é a
matriz m por p (m linhas e p colunas)
dada por:

28. Multiplicação

34. Matrizes booleanas
São matrizes que têm apenas elementos
iguais a 0 ou 1.
Podemos definir uma operação booleana
de multiplicação A×B para matrizes
booleanas usando multiplicação e soma
booleanas, ao invés de multiplicação e
adição usuais.

35. operações booleanas de multiplicação e adição

36.  A multiplicação
booleana de
matrizes A X B é
definida por:

39. EXERCÍCIOS
 Multiplicação de matrizes
 O número de transistores e o número de alto-
falantes usados para montar três modelos de
aparelhos de TV foram especificados em uma
tabela.