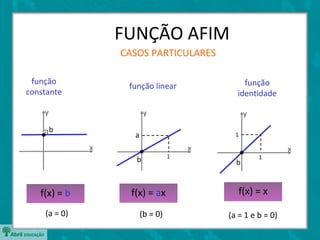
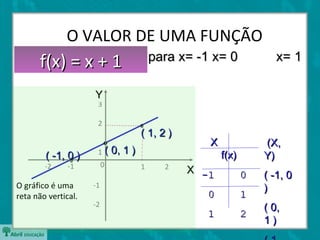
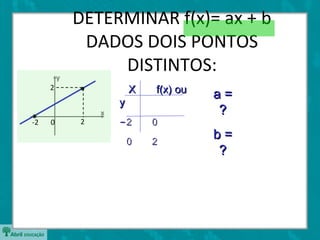
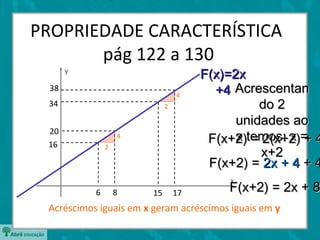
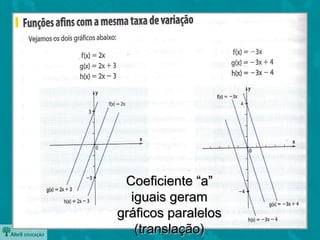
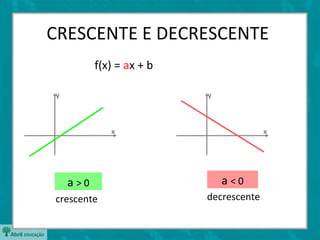
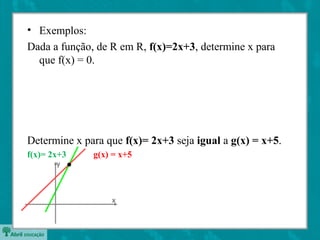
O documento descreve as funções afins, definindo-as como f(x)=ax+b e explicando os significados de a e b. Também apresenta casos particulares como funções constantes, lineares e identidade. Exemplifica como determinar a e b a partir de dois pontos e estudar o sinal da função.

1. FUNÇÃO AFIMFUNÇÃO AFIM
CAPÍTULO 4CAPÍTULO 4
PÁGINA 112PÁGINA 112

2. FUNÇÃO AFIM
f(x) = ax + b
a é a taxa de variação de f(x) em relação a x
Coeficiente angular da função.
b é o valor inicial de y f(0)=b
X é a variável.
Toda relação f(x), de R em R, dada por f(x)=ax+b,
com “a” e “b” números reais.

3. 0
y
x
FUNÇÃO AFIM – pag112 a 121
b
f: R em R | f(x) =f(x) = aax +x + bb
O gráfico é uma reta não
vertical.
D = R
CD = R
Im = R
f: R em R
Para a e bPara a e b
reaisreais

4. y
x
y
x
CASOS PARTICULARES
b
f(x) = b
(a = 0)
y
x
função
constante
função linear
f(x) = ax
(b = 0)
função
identidade
f(x) = x
(a = 1 e b = 0)
FUNÇÃO AFIM
a
1
1
1
b
b

5. f(x) = x + 1f(x) = x + 1
O gráfico é uma
reta não vertical.
0 1 2-2 -1
3
2
1
-1
-2
XX
f(x)f(x)
-1 0-1 0
0 10 1
1 21 2
O VALOR DE UMA FUNÇÃO
YY
XX
(X,(X,
Y)Y)
( -1, 0( -1, 0
))
( 0,( 0,
1 )1 )
( -1, 0 )( -1, 0 )
( 1, 2 )( 1, 2 )
( 0, 1 )( 0, 1 )
para x= -1para x= -1 x= 0x= 0 x= 1x= 1

6. y
x
2
20-2
X f(x) ouX f(x) ou
yy
-2 0-2 0
0 20 2
DETERMINAR f(x)= ax + b
DADOS DOIS PONTOS
DISTINTOS:
a =a =
??
b =b =
??

7. • Exemplo :
A- Dada f(x)=ax+b, de R em R, onde f(2)= -2 e f(1) = 1,
determine a lei de formação dessa função e construa seu
gráfico.
B- Uma fábrica possui um custo de produção fixo de R$120
reais e um custo variável de R$3,00 por peça produzida.
Escreva a relação que representa o custo C dessa fábrica em
função do número “n” de peças produzidas.

8. PROPRIEDADE CARACTERÍSTICA
pág 122 a 130
y
x
16
6
20
8
34
15
38
17
Acréscimos iguais em x geram acréscimos iguais em y
2
4
2
4
F(x)=2xF(x)=2x
+4+4 AcrescentanAcrescentan
do 2do 2
unidades aounidades ao
x temos: x =x temos: x =
x+2x+2
F(x+2) = 2(x+2) + 4F(x+2) = 2(x+2) + 4
F(x+2) =F(x+2) = 2x + 42x + 4 + 4+ 4
F(x+2) = 2x + 8F(x+2) = 2x + 8

9. Coeficiente “a”Coeficiente “a”
iguais geramiguais geram
gráficos paralelosgráficos paralelos
(translação)(translação)

10. CRESCENTE E DECRESCENTE
f(x) = ax + b
a > 0 a < 0
crescente decrescente
y
x
y
x

11. y
x
y
x
ZEROS DA FUNÇÃO AFIM : f(x) = ax + b
bb
bb
a
b
xxf
−
=⇒= 0)( bxfx =⇒= )(0
Corta o eixo x
Corta o eixo y
0)( =xf
0=x
Corta o eixo x
0)( =xf
Corta o eixo y
0=x

12. • Exemplos:
Dada a função, de R em R, f(x)=2x+3, determine x para
que f(x) = 0.
Determine x para que f(x)= 2x+3 seja igual a g(x) = x+5.
f(x)= 2x+3 g(x) = x+5
y
x

13. y
x
y
x
+ +
− −
ESTUDO DO SINAL – pág 131
f(x) > 0⇒x <
f(x) < 0⇒x < f(x) < 0⇒x >
f(x) > 0⇒x >
Crescente a>0Crescente a>0
Decrescente a<0Decrescente a<0
f(x) = 0⇒x = f(x) = 0⇒x =
a
b−
a
b−
a
b−
a
b−
a
b−
a
b−
a
b−
a
b−

14. x x
+ +
− −
ESTUDO DO SINAL
DISPOSITIVO PRÁTICO: não precisamos desenhar o eixo y
f(x) < 0⇒x <
f(x) > 0⇒x >
f(x) = 0⇒x =
a
b−
a
b−
a
b−
f(x) > 0⇒x <
f(x) < 0⇒x >
f(x) = 0⇒x =
a
b−
a
b−
a
b−
a
b−
a
b−

15. • EXEMPLO
• Dada as funções afins f(x)= - 4x-3 e
g(x)=2x- 8 faça o estudo do sinal de f(x) e
de g(x).

16. Sistema de Inequação
Dado o sistema de inequações
Sua solução será dada pela intersecção das soluções
das duas inequações.
xxx 2632 <+≤+−



<+
+≤+−
xx
xx
26
632

17. Inequações produto e quociente
Determine x para que f(x) > 0, dada
)22(
)1).(4(
)(
−
−+
=
x
xx
xf

18. 1,2, 3.........................................pag 113
6, 9, 10, 11................................pag 115
14, 15, 18, 19............................pag 116
29, 32, 34, 35, 39.....................pag 121
43, 50 , 51.................................pag 129
53, 54 e 56................................pág 132
87, 91, 92, 95............................pag 142
57, 58, 61 .................................pag 135
Exercícios: