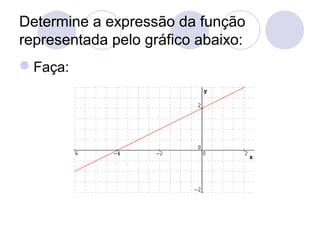
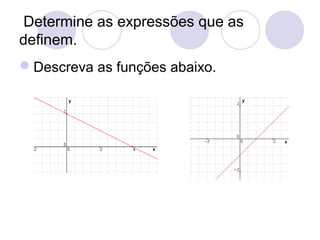
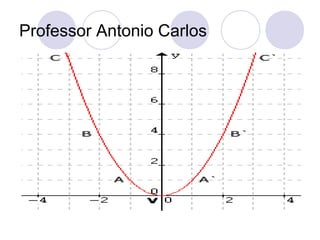
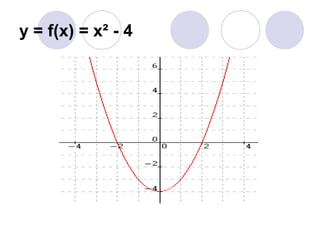
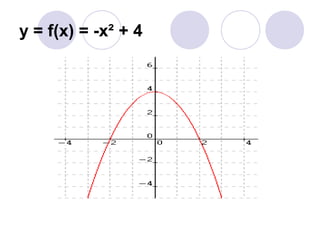
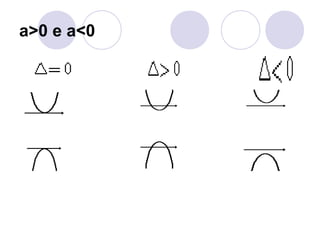
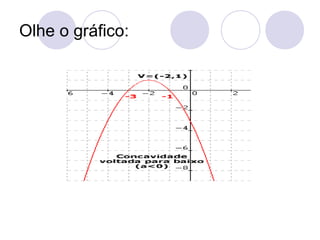
Este documento fornece um resumo sobre funções do 2o grau. Em três frases ou menos: A função do 2o grau é definida pela expressão y=ax2+bx+c, onde a, b e c são constantes. O gráfico de uma função quadrática é uma parábola, cujo vértice pode ser encontrado calculando -b/2a. O sinal de a determina se a concavidade da parábola está voltada para cima ou para baixo.

1. Função do 2º grau
Função do 2º grau
A função do 2º grau, também denominada
função quadrática, é definida pela expressão
do tipo:
y = f(x) = ax² + bx + c, onde a, b e c são
constantes reais e Exemplos:
a) y=x²+3x+2 ( a=1; b=3; c=2 )
b) y=x² ( a=1; b=0; c=0 )
c) y=x²-4 ( a=1; b=0; c=-4 )

2. Conteúdo para 8ª série
Professor Antonio Carlos Carneiro Barroso
Professor de Matemática do Colégio estadual
Dinah Gonçalves em Valéria Salvador-Ba
Graduado pela UFBA e pós graduado em
metodologia e Didática do Ensino Superior
www.ensinodematemtica.blogspot.com.br
www.profantoniocarneiro.com
www.accbarrosogestar.blogspot.com.br

3. Gráficos:
Gráfico de uma função do 2º grau:
O gráfico de uma função quadrática
é uma parábola
Podemos visualizar uma parábola em um
parque de diversões, simplesmente olhando
para a montanha russa.
 Sua representação gráfica é dada em torno de
eixos:

4. Veja:
A Parábola:

5. Professor Antonio Carlos

6. Observe os pontos:
 Notem que os pontos: A e A`, B e B`, C e C` são
simétricos (estão a mesma distância do eixo de
simetria). O ponto V representa o vértice da parábola, é
a partir dele que determinamos todos os outros pontos.
Coordenadas do vértice
 A coordenada x do vértice da parábola pode ser
determinada por .
 Exemplo: Determine as coordenada do vértice da
parábola y=x²-4x+3
Temos: a=1, b=-4 e c=3
Logo, a coordenada x será igual a 2, mas e a
coordenada y?

7. Fique atento:
Simples: Vamos substituir o valor obtido da coordenada
x e determinar o valor da coordenada y.
Assim, para determinarmos a coordenada y da parábola
y=x²-4x+3, devemos substituir o valor de x por 2.
y = (2)²-4.(2)+3 = 4-8+3=-1
Logo, as coordenadas do vértice serão V=(2,-1)
Portanto, para determinarmos as coordenadas do
vértice de uma parábola, achamos o valor da
coordenada x (através de x=-b/2a) e substituindo este
valor na função, achamos a coordenada y!!!

8. Raízes:
Raízes (ou zeros) da função do 2º grau
Denominam-se raízes da função do 2º grau os
valores de x para os quais ela se anula.
y=f(x)=0
Exemplo: na função y=x²-4x+3, que acima
acabamos de determinar as coordenadas de
seus vértices, as raízes da função serão x=1 e
x`=3.
Vejamos o gráfico:

9. O gráfico:

10. Resolva a função:
Notem que quando x=1 e x`=3, a parábola intercepta
("corta") o eixo x.
Como determinar a raiz ou zero da função do 2º
grau?
Simplesmente aplicando a resolução de equações do 2º
grau, já vista na seção anterior.
Exemplo: determine a raiz da função y=x²+5x+6:
Fazendo y=f(x)=0, temos x²+5x+6=0
Agora basta resolver a equação aplicando a fórmula de
Bháskara.
x²+5x+6=0
Acharemos que x = -2 e x` = -3.

11. Concavidade da parábola
Explicarei esta parte com um simples desenho.
a>0a<0Os desenhos até que ficaram bonitinhos,
mas isso não importa neste momento. O que
nos importa agora é que quando a>0, a
concavidade da parábola está voltada para cima
(carinha feliz) e quando a<0, a parábola está
voltada para baixo (carinha triste).
Exemplos:

12. y = f(x) = x² - 4

13. y = f(x) = -x² + 4

14. Nota:
Quando a concavidade está voltada para cima (a>0), o
vértice representa o valor mínimo da função. Quando a
concavidade está voltada para baixo (a<0), o vértice
representa o valor máximo.
Quando o discriminante é igual a zero
Quando o valor de , o vértice a parábola encontra-se no
eixo x. A coordenada y será igual a zero.
Exemplo: y=f(x)=x²+2x+1
x²+2x+1=0
x=x`=-b/2a=-1
As coordenadas do vértice serão V=(-1,0)

15. Gráfico:

16. Estudo do delta:
Quando o descriminante é maior que zero
Quando o valor de , a parábola intercepta o eixo
x em dois pontos. (São as raízes ou zeros da
função vistos anteriormente).
Exemplo: y = f(x) = x²-4x+3
x²-4x+3=0
x=1, x`=3
Gráfico:

17. Gráfico:

18. Delta<0
Quando o discriminante é menor que
zero
Quando o valor de , a parábola não
intercepta o eixo x. Não há raízes ou
zeros da função.
Exemplo: y = f(x) = x²-x+2
x²-x+2=0

19. Gráfico:

20. a>0 e a<0

21. Olhe o gráfico:
Esboçando o gráfico
Para finalizarmos (ufa!), vamos desenhar
o gráfico da função
y=-x²-4x-3
1ª etapa: Raízes ou zeros da função
-x²-4x-3=0
Aplicando a fórmula de Bháskara
x=-1, x`=-3

22. Veja as etapas:
2ª etapa: Coordenadas do vértice
Coordenada x (=-b/2a): -(-4)/2.(-1)=-2
Coordenada y: Basta substituir o valor de x
obtido na função
y = -x²-4x-3 = -(-2)²-4.(-2)-3 = -4+8-3 = 1
Portanto, V=(-2,1)
3ª etapa: Concavidade da parábola
y=-x²-4x-3
Como a=-1<0, a concavidade estará voltada
para baixo

23. Olhe o gráfico:

24. Exercício:
1) As equações abaixo definem funções
do 2º grau. Para cada uma dessas
funções, ache as coordenadas do vértice
que a representa:
a) f(x)= x² - 4x + 5
b) f(x)= x² +4x - 6
c) f(x)= 2x² +5x - 4
d) f(x)= -x² + 6x - 2
e) f(x)= -x² - 4x +1

25. Resolva:
2) Determine, se existirem, os zeros reais
das funções seguintes:
a) f(x)= 3x² - 7x + 2
b) f(x)= -x² + 3x - 4
c) f(x)= -x² + 3/2x + 1
d) f(x)= x² -4
e) f(x)= 3x²
Não existe zeros em (b)

26. Antonio Carlos carneiro Barroso:
3) Construa o gráfico das seguintes
funções:
a) f(x)= x² - 16x + 63
b) f(x)= 2x² - 7x + 3
c) f(x)= 4x² - 4x +1
d) f(x)= -x² + 4x - 5
e) f(x)= -2x² +8x- 6

27. Faça:
4) Em uma partida de vôlei, um jogador deu um
saque em que a bola atingiu uma altura h em
metros, num tempo t, em segundos, de acordo
com a relação h(t) = -t² + 8t.
a) Em que instante a bola atingiu a altura
máxima?
[Nota]: observem o vértice
b) De quantos metros foi a altura máxima
alcançada pela bola?
c) Esboce o gráfico que represente esta
situação.
Respostas: 4: a)4s; b) 16m

28. Função do 1º grau:
Vamos iniciar o estudo da função do 1º grau, lembrando
o que é uma correspondência:
Correspondência: é qualquer conjunto de pares
ordenados onde o primeiro elemento pertence ao
primeiro conjunto dado e o segundo elemento pertence
ao segundo conjunto dado.
Assim: Dado os conjuntos A={1,2,3} e B={1,2,3,4,5,6}
consideremos a correspondência de A em B, de tal
modo que cada elemento do conjunto A se associa no
conjunto B com o seu sucessor. Assim ; ; . A
correspondência por pares ordenados seria:


29. Noção de função:
Veja os diagramas:

30. Uma função todo elemento de A tem
imagem única em B.
Analisando os diagramas acima:
O diagrama 1 não satisfaz a condição (1);
os diagramas 3, 4 e 5 não satisfazem a
condição (2).
Logo, somente o diagrama 2 representa
uma função

31. Domínio, imagem e contra domínio
Observe o diagrama:

32. Função:
 Chamemos esta função de f, logo o conjunto de pares ordenados
serão:
 f={(1,2),(2,3),(3,4)}
 O conjunto X={1,2,3} denomina-se domínio da função f.
 D(F)=X
 O conjunto Y={1,2,3,4,5} denomina-se contradomínio da função f.
 C(F)=Y
 Dizemos que 2 é a imagem de 1 pela função f.
 f(1)=2
 Ainda, f(2)=3 e f(3)=4.
 Logo o conjunto das imagens de f e dado por:
 Im(f)={2,3,4}

33. Determinação de função:
Observe a figura:

34. Veja:
Associe cada elemento de X com um
elemento de y:

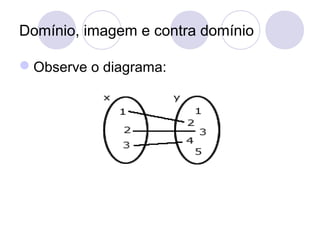
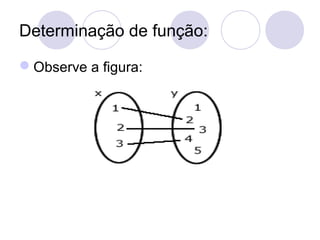
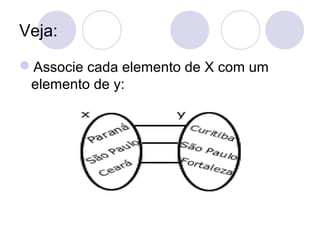
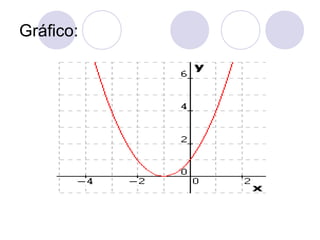
35. Determine a imagem de cada função:
a) D(f) = {1,2,3}
y = f(x) = x + 1
[Sol] f(1) = 1+1 = 2
f(2) = 2+1 = 3
f(3) =3+1 = 4
Logo: Im(f)={2,3,4}
b) D(f) = {1,3,5}
y = f(x) = x²
[Sol] f(1) = 1² = 1
f(3) = 3² = 9
f(5) = 5² = 25
Logo: Im(f)={1,9,25}

36. Plano cartesiano :
Eixo Cartesiano:

37. Eixos x e y:
Consideremos dois eixos x e y
perpendiculares em 0, os quais
determinam o plano A.
Dado um plano P qualquer, pertencente
ao plano A, conduzamos por ele duas
retas:
x // x' e y // y'
Denominemos P1 a interseção de x com
y' e P2 a interseção de y com x'

38. Continuação:
Nessas condições, definimos:
- Abscissa de P é um número real representado por P1
- Ordenada de P é um número real representado por P2
- A coordenada de P são números reais x' e y' ,
geralmente indicados na forma de par ordenado ( x' , y' )
- O eixo das abscissas é o eixo x
- O eixo das ordenadas é o eixo y
- A origem do sistema é o ponto 0
- Plano cartesiano é o plano A.

39. Depois dessa revisão veja a função do 1º
grau:
Exemplo:
Numa loja, o salário fixo mensal de um
vendedor é 500 reais. Além disso, ele recebe de
comissão 50 reais por produto vendido.
a) Escreva uma equação que expresse o ganho
mensal y desse vendedor, em função do
número x de produto vendido.
[Sol] y=salário fixo + comissão
y=500 + 50x

40. Cont.
Quanto ele ganhará no final do mês se
vendeu 4 produtos?
[Sol] y=500+50x , onde x=4
y=500+50.4 = 500+200 = 700
Quantos produtos ele vendeu se no final
do mês recebeu 1000 reais?
[Sol] y=500+50x , onde y=1000
1000=500+50x » 50x=1000-500 »
50x=500 » x=10

41. Cont.
A relação assim definida por uma
equação do 1º grau é denominada função
do 1º grau, sendo dada por:
y=f(x)=ax+b com ,a e b pertencente
aos números reais


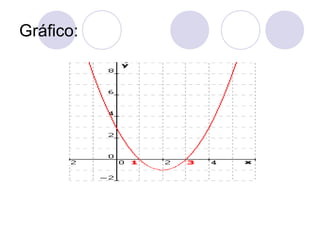
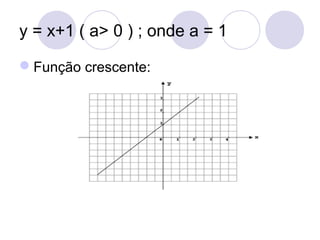
42. Gráfico:
Gráfico da função do 1º grau:
O gráfico de uma função do 1º grau de R em R
é uma reta.
Exemplo:
1) Construa o gráfico da função determinada por
f(x)=x+1:
[Sol] Atribuindo valores reais para x, obtemos
seus valores correspondentes para y.

43. Olhe os pares:
O conjunto dos pares ordenados determinados é f={(-2,-1),
(-1,0),(0,1),(1,2),(2,3)}

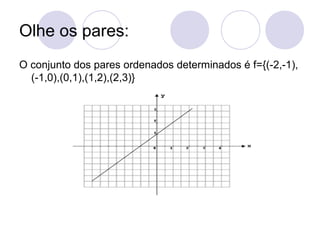
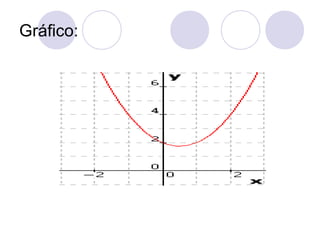
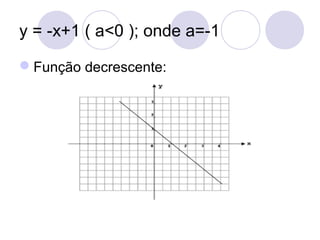
44. 2º Exemplo:
Construa o gráfico da função determinada por
f(x)=-x+1.
[Sol] Atribuindo valores reais para x, obtemos
seus valores correspondentes para y.
xy=f(x)=-x+1-2 3-1 20 11 02-1O conjunto dos
pares ordenados determinados é f={(-2,3),(-1,2),
(0,1),(1,0),(2,-1)}

45. Continuação:
O gráfico:

46. y = x+1 ( a> 0 ) ; onde a = 1
Função crescente:

47. y = -x+1 ( a<0 ); onde a=-1
Função decrescente:

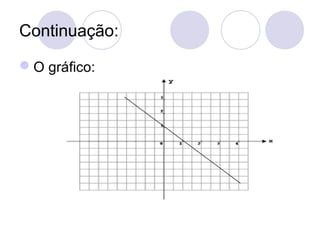
48. Raízes ou zeros:
Para determinarmos a raiz ou zero de uma
função do 1º grau, definida pela equação
y=ax+b, como a é diferente de 0, basta
obtermos o ponto de intersecção da equação
com o eixo x, que terá como coordenada o par
ordenado (x,0).
1) Considere a função dada pela equação
y=x+1, determine a raiz desta função.
[Sol] Basta determinar o valor de x para termos
y=0
x+1=0 » x=-1
Dizemos que -1 é a raiz ou zero da função

49. Veja a raiz dessa função:
Onde corta o eixo x é a raiz da função

50. Determine a raiz da função y=-x+1 e
esboce o gráfico
Veja:

51. Sinal de uma função de 1º grau
 a>o e a<o

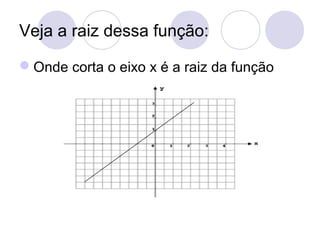
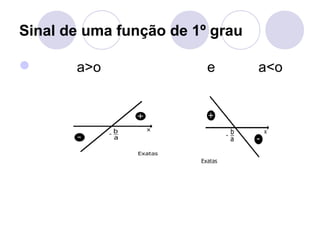
52. Cont.
Note que para x=-b/a, f(x)=0 (zero da função).
Para x>-b/a, f(x) tem o mesmo sinal de a. Para
x<-b/a, f(x) tem o sinal contrário ao de a.
Exemplos:
1) Determine o intervalo das seguintes funções
para que f(x)>0 e f(x)<0.
a) y=f(x)=x+1
[Sol] x+1>0 » x>-1
Logo, f(x) será maior que 0 quando x>-1
 x+1<0 » x<-1
Logo, f(x) será menor que 0 quando x<-1

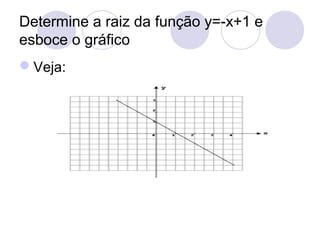
53. 2º exemplo:
b) y=f(x)=-x+1
[Sol]* -x+1>0 » -x>-1 » x<1
Logo, f(x) será maior que 0 quando x<1
 -x+1<0 » -x<-1 » x>1
Logo, f(x) será menor que 0 quando
x>1
(*ao multiplicar por -1, inverte-se o sinal
da desigualdade

54. Exercício:
) Represente graficamente a função
definida por:
a) f(x) = 2x-1
b) f(x) = -1/2x+3
c) f(x) = 4x
d) f(x) = 1/3x+2
e) f(x) = -3x+6

55. Cont.
2) Determine a raiz ou zero de cada uma
das seguintes equações:
a) f(x) = 2x+5
b) f(x) = -x+2
c) f(x) = 1/3x+3
d) f(x) = 1-5x
e) f(x) = 4x

56. Determine a expressão da função
representada pelo gráfico abaixo:
Faça:

57. Cont.
Pelo gráfico, concluímos:
Quando x=0, y=2; portanto, o valor de b na
expressão é igual a 2
Quando y=0, x=-4 (raiz ou zero da função)
Substituindo os valores em y=ax+b:
0 = -4a + 2
a = 1/2
Logo, a expressão é y = 1/2x+2.

58. Determine as expressões que as
definem.
Descreva as funções abaixo.