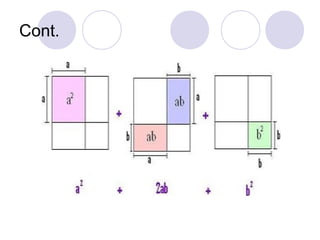
O documento apresenta os principais produtos notáveis em álgebra, incluindo o quadrado da soma, quadrado da diferença, produto da soma pela diferença, cubo da soma e cubo da diferença. Explica como resolver cada um através da propriedade distributiva ou de regras práticas, com exemplos como (a + b)2 = a2 + 2ab + b2.

1. Produtos Notáveis:
Produtos notáveis são produtos de
expressões algébricas que possuem
uma forma geral para sua resolução.
Os produtos abaixo são exemplos, em
forma geral, de produtos notáveis:
(a + b) . (a + b) = (a + b)2 Quadrado
da soma
(a – b) . (a – b) = (a – b)2
Quadrado da diferença

2. Continuação:
(a + b) . (a – b) Produto da soma pela diferença
(x + p) . (x + q) Produto do tipo
(a + b) . (a + b) . (a + b) = (a + b)3 Cubo da soma
(a – b) . (a – b) . (a – b) = (a – b)3 Cubo da diferença
Tem duas formas de provar como resolver o quadrado
da soma. A primeira é resolvendo algebricamente, veja
como: (a + b)2 é o mesmo que (a + b) . (a + b) Então,
utilizando a propriedade distributiva vamos calcular:
(a + b) . (a + b) ------ utilizando a propriedade distributiva.

3. a 2 + ab + ab + b 2 ------ operar os termos
semelhantes.
a 2 + 2ab + b 2 Concluímos que: (a + b) .
(a + b) = (a + b)2 A segunda forma é
geometricamente, veja como: Observe o
quadrado de lado (a + b) e calculemos a
sua área.

4. Veja:

5. Professor Antonio Carlos

6. Cont.

7. Veja:
Concluímos que (a + b)2 = a 2 + 2ab + b
2

(a + b)2 = quadrado do primeiro termo
mais duas vezes o primeiro vezes o
segundo mais o quadrado do segundo
termo

8. Produtos Notáveis:
Algumas multiplicações envolvendo expressões
algébricas revelam certos padrões matemáticos
em suas resoluções. Essas expressões são
conhecidas como produtos notáveis, que se
dividem em quadrado da soma, quadrado da
diferença, produto da soma pela diferença, cubo
da soma e cubo da diferença. Desses,
destacaremos a nossa atenção para o quadrado
da diferença e seu desenvolvimento.

9. Quadrado da Diferença:
As expressões que possuem a forma (a –
b)2 podem ser resolvidas de duas formas
distintas: aplicando a propriedade
distributiva da multiplicação ou a regra
prática. Utilizando a propriedade
distributiva na expressão (a – b)2. Pela
definição de potenciação sabemos que (a
– b)2 pode ser escrito na forma (a – b)*
(a – b). (a – b)* (a – b) = a*a – a*b – b*a
+ b*b = a² – 2ab + b²

10. Cont.
(x – 4)² = (x – 4) * (x – 4) = x*x – 4*x – 4*x
+ 4*4 = x² – 8x + 16 (2y – 5)² = (2y – 5) *
(2y – 5) = 2y*2y – 2y*5 – 5*2y + 5*5 = 4y²
– 20y + 25 (5a – 2b)² = (5a – 2b) * (5a –
2b) = 5a*5a – 5a*2b – 2b*5a + 2b*2b =
25a² – 20ab + 4b² Utilizando a regra
prática na expressão (a – b)2.

11. Cont.
O quadrado do primeiro termo menos,
duas vezes o primeiro termo vezes o
segundo termo, mais o quadrado do
segundo termo.” (y – 6)² = (y)² – 2*y*6 +
(6)² = y² – 12y + 36 (4b – 9)² = (4b)² –
2*4b*9 + (9)² = 16b² – 72b + 81
(7y – 6x)² = (7y)² – 2*7y*6x + (6x)² = 49y²
– 84xy + 36x² (10x – 2z)² = (10x)² –
2*10x*2z + (2z)² = 100x² – 40xz + 4z²

12. Cont.
Uma situação interessante envolvendo
expressões algébricas se apresenta na seguinte
forma: (a + b)(a – b), sendo denominada
Produto da Soma pela Diferença, podendo ser
resolvida através da propriedade distributiva da
multiplicação ou através de uma regra prática.
Essa expressão pode ser considerada um
produto notável, pela característica regular
apresentada na resolução de situações
semelhantes

13. Diferença de dois quadrados.
Essa expressão pode ser considerada um produto
notável, pela característica regular apresentada
distributiva na resolução da expressão (a + b)(a – b).
(a + b)(a – b) = a*a – a*b + b*a – b*b = a² – b²
Note que os termos – ab e + ba são opostos, por isso se
anulam. (2x + 4)(2x – 4) = 2x*2x – 2x*4 + 4*2x – 4*4 =
4x² – 8x + 8x – 16 = 4x² – 16 (7x + 6)(7x – 6) = 7x*7x –
7x*6 + 6*7x – 6*6 = 49x² – 42x + 42x – 36 = 49x² – 36
(10x³ – 12)(10x³ + 12) = 10x³*10x³ + 10x³*12 – 12*10x³ –
12*12 = 100x6 + 120x³ – 120x³ – 144 = 100x6 – 144
(20z + 10x)(20z – 10x) = 20z*20z – 20z*10x + 10x*20z –
10x*10x = 400z² – 200zx + 200xz – 100x² = 400z² –
100x² na resolução de situações semelhantes.

14. Cont.
 Aplicando a propriedade Aplicando a regra
prática A aplicação da regra prática se dá
através da seguinte situação: “o primeiro termo
elevado ao quadrado menos o segundo termo
elevado ao quadrado” (4x + 7)(4x – 7) = (4x)² –
(7)² = 16x² – 49
(12x + 8)(12x – 8) = (12x)² – (8)² = 144x² – 64
(11x² – 5x)(11x² + 5x) = (11x²)² – (5x)² = 121x4 –
25x²
(20b – 30)(20b + 30) = (20b)² – (30)² = 400b² –
900

15. Cubo da soma:
Cubo da Soma
Temos que a expressão (a + b)³ pode ser
escrita da seguinte forma: (a + b)² * (a + b). A
decomposição permite aplicarmos o quadrado
da soma na expressão (a + b)², multiplicando o
resultado pela expressão (a + b). Veja: (a + b)² =
a² + 2ab + b² → (a² + 2ab + b²) * (a + b) = a²*a +
a²*b + 2ab*a + 2ab*b + b²*a + b²*b a³ + a²b +
2a²b + 2ab² + ab² + b³ → a³ + 3a²b + 3ab² + b³
(2x + 3)³ = (2x + 3)² * (2x + 3)

16. Cont.
(2x + 3)² = (2x)² + 2*2x*3 + (3²) = 4x² +
12x + 9
(4x² + 12x + 9) * (2x + 3) = 4x²*2x + 4x²*3
+ 12x*2x + 12x*3 + 9*2x + 9*3 = 8x³ +
12x² + 24x² + 36x + 18x + 27 = 8x³ + 36x²
+ 54x vezes o quadrado do primeiro termo
vezes o segundo termo mais três vezes o
primeiro termo vezes o quadrado do
segundo termo mais o cubo do + 27

17. Cont.
Regra Prática “O cubo do primeiro
termo mais três segundo termo.” (x + 3)³ =
(x)³ + 3*(x)²*3 + 3*x*(3)² + (3)³ = x³ + 9x² +
27x³ + 27 (2b + 2)³ = (2b)³ + 3*(2b)²*2 +
3*2b*(2)² + (2)³ = 8b³ + 24b² + 24b + 8

18. Cubo da diferença:
Cubo da Diferença O cubo da diferença pode ser
desenvolvido de acordo com os princípios resolutivos do
cubo da soma. A única alteração a ser efetuada é
quanto à utilização do sinal negativo. Observe: Regra
prática “O cubo do primeiro termo menos três vezes o
quadrado do primeiro termo vezes o segundo termo
mais três vezes o primeiro termo vezes o quadrado do
segundo termo menos o cubo do segundo termo.” (x –
3)³ = (x)³ – 3*(x)²*3 + 3*x*(3)² – (3)³ = x³ – 9x² + 27x³ –
27 (2b – 2)³ = (2b)³ – 3*(2b)²*2 + 3*2b*(2)² – (2)³ = 8b³ –
24b² +24– 8

19. Professor Antonio Carlos Carneiro
Barroso
Professor de Matemática do Colégio
Estadual Dinah Gonçalves em Valéria
Salvador-Ba
Graduado pela UFBA
Pós Graduado em Metodologia e Didática
10/10/2013
www.ensinodematemtica.blogspot.com.br
www.profantoniocarneiro.com