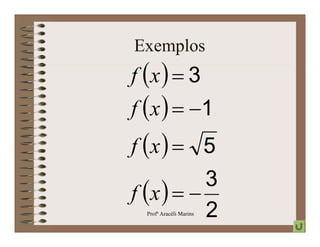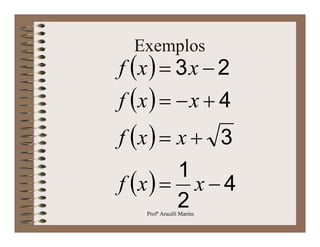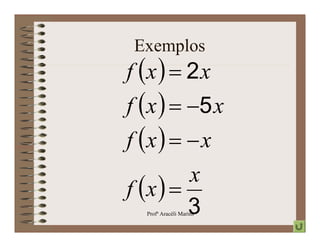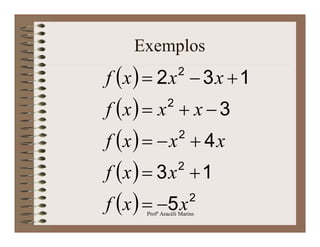O documento apresenta os conceitos básicos de funções polinomiais, incluindo funções constantes, afins, lineares e quadráticas. É descrito o formato de cada função, como plotar seus gráficos e encontrar raízes. Exemplos ilustram como aplicar esses conceitos.

1. Aula 4
Funções Polinomiais
Profª Aracéli Marins

2. Funções Polinomiais
• Função Constante
• Função Afim
• Função Linear
• Função Quadrática
Profª Aracéli Marins

3. Função Constante
• É toda função em que y não
sofre variação quando x varia,
ou seja, o valor de y continua
constante para todos os valores
de x.
• É escrita como f(x) = c
Profª Aracéli Marins

4. Gráfico de uma função constante
y
• Seu gráfico é
uma reta c
paralela ao
x
eixo x, que
intercepta o
eixo y em c.
Profª Aracéli Marins

5. Exemplos
f x   3
f  x   1
f x   5
3
2
f x   
Profª Aracéli Marins

6. Função Afim
• É também conhecida como
função do 1º grau.
• É toda função do tipo:
f(x) = ax + b
com a ≠ 0
Profª Aracéli Marins

7. Gráfico de uma função Afim
• O gráfico de uma função afim é
sempre uma reta;
• a é chamado coeficiente angular
ou inclinação da reta;
• a é o valor que representa a taxa
de variação de y com respeito a
Profª Aracéli Marins
x.

8. Gráfico de uma função Afim
y
• b é conhecido como
coeficiente linear tg á = a
da reta;
• b é o número no á
qual a reta b
x
intercepta o eixo y.
Profª Aracéli Marins

9. Raiz
• A raiz da função afim é:
b
x
a
Profª Aracéli Marins

10. Exemplos
f x   3 x  2
f x    x  4
f x   x  3
1
f x   x  4
2
Profª Aracéli Marins

11. Exemplos
• O salário fixo mensal de um segurança é de
R$ 560,00. Para aumentar sua receita, ele
faz plantões noturnos em uma boate, onde
recebe R$ 60,00 por noite de trabalho.
– Se em um mês ele fizer 3 plantões, que
salário receberá?
– Qual é o salário final y, quando ele
realiza x plantões?
Profª Aracéli Marins

12. Função Linear
y
• São funções
afim com
b = 0.
• Ou seja:
f(x) = ax x
• Seu gráfico
sempre passa
pela origemProfª Aracéli Marins

13. Exemplos
f x   2 x
f  x   5 x
f x    x
x
3
f x  
Profª Aracéli Marins

14. Função Quadrática
• É uma função polinomial de
grau 2;
• É escrita como:
2
f x  ax  bx  c
com a ≠ 0
Profª Aracéli Marins

15. Gráfico
• O gráfico
de uma
função do
2º grau é
uma
parábola
Profª Aracéli Marins

16. Raízes
• São obtidas com o uso da
fórmula:
2
 b  b  4ac
x1, 2
2a

Profª Aracéli Marins

17. Observação
Usualmente, alguns autores
denotam b 2  4ac por:
Assim:

2
  b  4ac
Profª Aracéli Marins

18. Exemplos
2
f x   2 x  3 x  1
2
f x   x  x  3
2
f x    x  4 x
2
f x   3 x  1
2
f x   5 x
Profª Aracéli Marins

19. Concavidade do gráfico da
Função Quadrática
• Se a > 0, a parábola tem
concavidade voltada para cima e
um ponto mínimo V;
• Se a < 0, a parábola tem
concavidade voltada para baixo e
um ponto máximo V.
Profª Aracéli Marins

20. Coordenadas do vértice da
parábola
As coordenadas do vértice são:
b ;
2a
x
 .
4a
y
Independente do sinal de a.
Profª Aracéli Marins

21. A construção da parábola
Para construir a parábola, seguir os passos:
• Verificar a concavidade utilizando a;
• Verificar o local em que a parábola intercepta o
eixo x utilizando os zeros;
• Calcular as coordenadas do vértice;
• Traçar a reta que passa por V e é paralela ao eixo
y, que é o eixo de simetria da parábola;
• c é o local em que a parábola intercepta o eixo y.
Profª Aracéli Marins

22. Exemplos
• Construir o gráfico das funções f, utilizando
as instruções anteriores:
2
f x   x  2 x  3
2
f x    x  4 x  4
2
f x   x  2 x  2
Profª Aracéli Marins

23. Exercícios
1- Faça o gráfico de cada uma das funções:
2
f x    x  2 x  8
2
f x   x  6 x  9
2
f x   x  x  6
Profª Aracéli Marins

24. Exercícios
2 - A parábola f(x) = x2 - 4x + 3 e a reta
f(x) = ax + b cruzam os eixos cartesianos
nos mesmos pontos. Qual é a equação da
reta?
3 - Páginas 35 – 36: 1, 2, 8, 9, 10, 12 do livro
do Stwart.
Profª Aracéli Marins