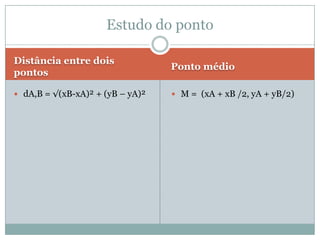
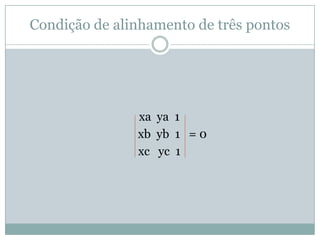
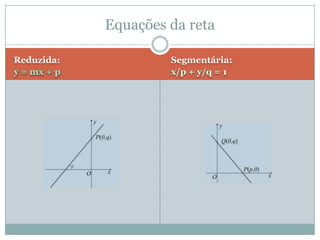
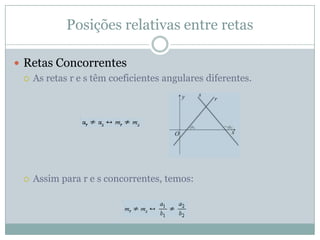
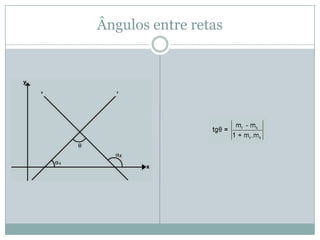
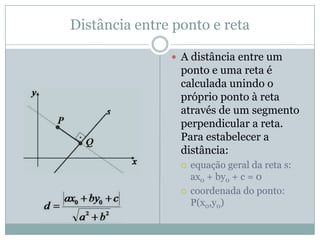
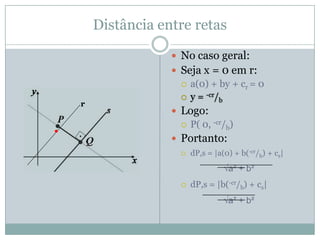
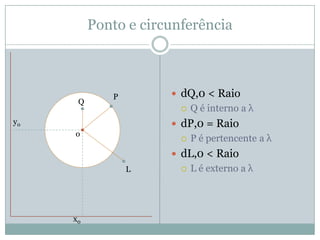
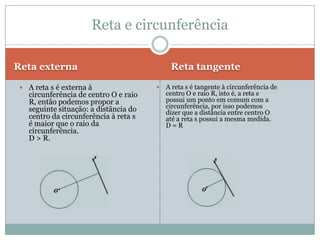
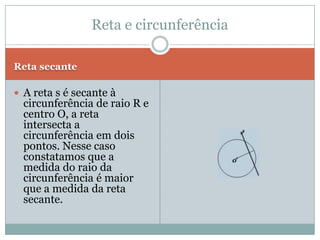
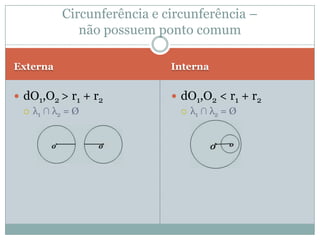
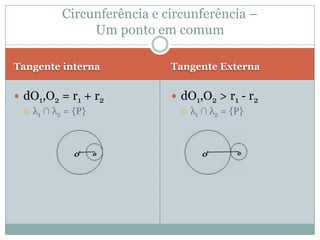
O documento discute conceitos geométricos como ponto, reta e circunferência. Apresenta fórmulas para calcular distância entre pontos e ponto médio, equações de retas e circunferências, e relações entre essas figuras geométricas como posições relativas, ângulos e distâncias.

1. Ponto, reta e circunferênciaGeometria Analítica

2. Distância entre dois pontosPonto médioRazão de secçãoCondição de alinhamento de três pontosEstudo do ponto

3. Distância entre dois pontosPonto médiodA,B = √(xB-xA)² + (yB – yA)² M = (xA + xB /2, yA + yB/2)Estudo do ponto

4. Origem, e extremidadePonto divisorOP = r PE Estudo do ponto – Razão de secção

5. Condição de alinhamento de três pontosxaya 1xbyb 1 = 0xc yc 1

6. Equações da retaPosições relativas entre retasÂngulos entre retasDistância entre ponto e reta

7. RetasInequações no planoEstudo da reta

8. Reduzida:y = mx + pSegmentária:x/p + y/q = 1Equações da reta

9. Equação geral: ax + by + c = 0Equação fundamental:y - yA = m (X- XA)Equações da reta

10. Posições relativas entre retasRetas ParalelasAs retas r e s têm o mesmo coeficiente angular.Assim para r//s, temos:

11. Posições relativas entre retasRetas ConcorrentesAs retas r e s têm coeficientes angulares diferentes.Assim para r e s concorrentes, temos:

12. Posições relativas entre retasRetas PerpendicularesÉ um caso particular de reta concorrente. Duas retas são ditas perpendiculares quando os seus coeficientes angulares são tais que:

13. Ângulos entre retas

14. Distância entre ponto e retaA distância entre um ponto e uma reta é calculada unindo o próprio ponto à reta através de um segmento perpendicular a reta. Para estabelecer a distância:equação geral da reta s: ax0 + by0 + c = 0coordenada do ponto: P(x0,y0)

15. Distância entre retasNo caso geral:Seja x = 0 em r:a(0) + by + cr= 0y = -cr/bLogo:P( 0, -cr/b)Portanto:dP,s = |a(0) + b(-cr/b) + cs|√a² + b²dP,s = |b(-cr/b) + cs|√a² + b²r

16. Equação geral e reduzida da circunferênciaPosições relativas Ponto e circunferência Reta e circunferência Circunferência e circunferênciaEstudo da circunferência

17. Equações da circunferência Geralx² – 2xa + a² + y² - 2by + b² = r²Reduzida r2 = (x – a)2 + (y – b)2

18. Ponto e circunferênciadQ,0 < RaioQ é interno a λdP,0 = RaioP é pertencente a λdL,0 < RaioL é externo a λPQy0oLx0

19. Reta externaReta tangenteA reta s é externa à circunferência de centro O e raio R, então podemos propor a seguinte situação: a distância do centro da circunferência à reta s é maior que o raio da circunferência. D > R.A reta s é tangente à circunferência de centro O e raio R, isto é, a reta s possui um ponto em comum com a circunferência, por isso podemos dizer que a distância entre centro O até a reta s possui a mesma medida. D = R Reta e circunferência

20. Reta secanteA reta s é secante à circunferência de raio R e centro O, a reta intersecta a circunferência em dois pontos. Nesse caso constatamos que a medida do raio da circunferência é maior que a medida da reta secante.Reta e circunferência

21. ExternaInternadO1,O2 > r1 + r2λ1 ∩ λ2 = ØdO1,O2 < r1 + r2λ1 ∩ λ2 = ØCircunferência e circunferência – não possuem ponto comum

22. Tangente internaTangente ExternadO1,O2 = r1 + r2λ1 ∩ λ2 = {P}dO1,O2 > r1 - r2λ1 ∩ λ2 = {P}Circunferência e circunferência –Um ponto em comum