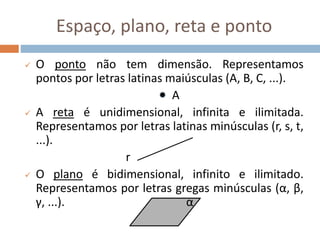
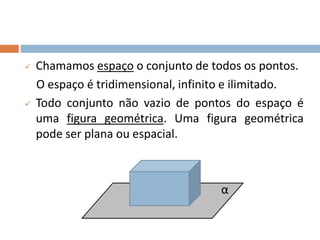
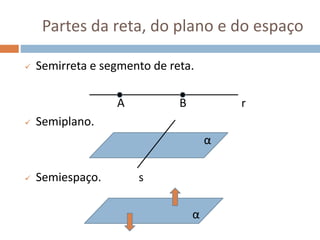
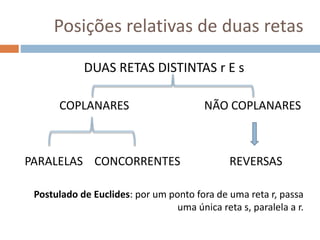
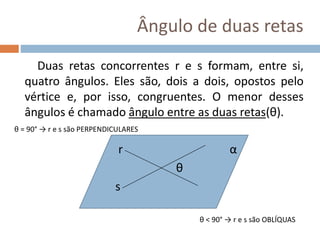
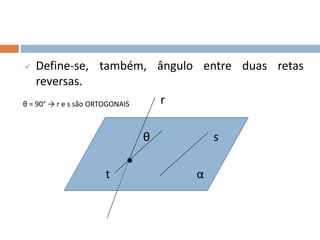
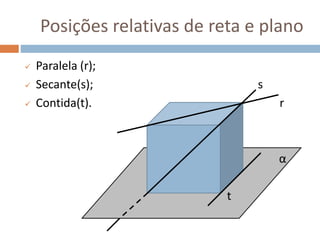
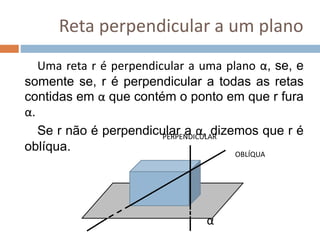
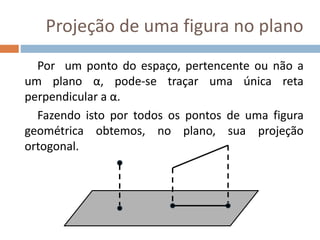
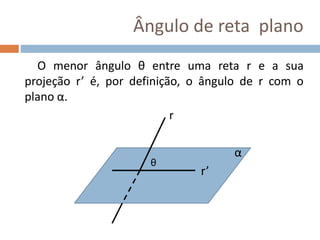
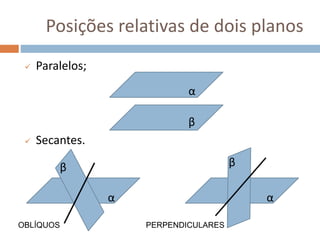
Este documento apresenta conceitos básicos de geometria espacial, incluindo definições de ponto, reta, plano e espaço, bem como suas posições relativas. Detalha postulados fundamentais e conceitos como paralelismo, perpendicularidade e ângulos entre retas e planos. Por fim, aborda noções de distância no espaço entre pontos e retas ou pontos e planos.

1. GEOMETRIA
ESPACIAL DE POSIÇÃO
Escola SESC de Ensino Médio
Equipe de Matemática 2015-2017

2. Espaço, plano, reta e ponto
 O ponto não tem dimensão. Representamos
pontos por letras latinas maiúsculas (A, B, C, ...).
A
 A reta é unidimensional, infinita e ilimitada.
Representamos por letras latinas minúsculas (r, s, t,
...).
r
 O plano é bidimensional, infinito e ilimitado.
Representamos por letras gregas minúsculas (α, β,
γ, ...). α

3.  Chamamos espaço o conjunto de todos os pontos.
O espaço é tridimensional, infinito e ilimitado.
 Todo conjunto não vazio de pontos do espaço é
uma figura geométrica. Uma figura geométrica
pode ser plana ou espacial.
α

4. Postulados e definições
 Postulado 1: Numa reta, bem como fora dela, há
infinitos pontos.
 Postulado 2: Por dois pontos distintos, passa uma
única reta.
 Postulado 3: Num plano, bem como fora dele,
existem infinitos pontos.
 Postulado 4: Por dois pontos distintos (ou pela reta
que eles determinam), passam infinitos planos.
 Postulado 5: Por três pontos distintos não
colineares, passa um único plano.
 Postulado 6: Se dois pontos distintos pertencem a
um plano, então, a reta que eles determinam está
contida no plano.

5. Partes da reta, do plano e do espaço
 Semirreta e segmento de reta.
A B r
 Semiplano.
α
 Semiespaço. s
α

6. Posições relativas de duas retas
DUAS RETAS DISTINTAS r E s
COPLANARES NÃO COPLANARES
PARALELAS CONCORRENTES REVERSAS
Postulado de Euclides: por um ponto fora de uma reta r, passa
uma única reta s, paralela a r.

7. r
s
t

8. Ângulo de duas retas
Duas retas concorrentes r e s formam, entre si,
quatro ângulos. Eles são, dois a dois, opostos pelo
vértice e, por isso, congruentes. O menor desses
ângulos é chamado ângulo entre as duas retas(θ).
r α
θ
s
θ = 90° → r e s são PERPENDICULARES
θ < 90° → r e s são OBLÍQUAS

9.  Define-se, também, ângulo entre duas retas
reversas.
r
θ s
t α
θ = 90° → r e s são ORTOGONAIS

10. Determinação do plano
Um plano fica determinado por:
 Uma reta e um ponto não pertencente a ela;
 Duas retas paralelas;
 Duas retas concorrentes.

11. Posições relativas de reta e plano
 Paralela (r);
 Secante(s); s
 Contida(t). r
α
t

12. Reta perpendicular a um plano
Uma reta r é perpendicular a uma plano α, se, e
somente se, r é perpendicular a todas as retas
contidas em α que contém o ponto em que r fura
α.
Se r não é perpendicular a α, dizemos que r é
oblíqua.
α
PERPENDICULAR
OBLÍQUA

13. Projeção de uma figura no plano
Por um ponto do espaço, pertencente ou não a
um plano α, pode-se traçar uma única reta
perpendicular a α.
Fazendo isto por todos os pontos de uma figura
geométrica obtemos, no plano, sua projeção
ortogonal.

14. Ângulo de reta plano
O menor ângulo θ entre uma reta r e a sua
projeção r’ é, por definição, o ângulo de r com o
plano α.
r
α
r’
θ

15. Posições relativas de dois planos
 Paralelos;
 Secantes.
α
β
αα
β β
OBLÍQUOS PERPENDICULARES

16. Se uma reta r é perpendicular a uma plano α, todo
plano que contenha r é perpendicular a α.

17. Ângulo de dois planos
Escolhendo um ponto P qualquer de r, traçamos,
por P, as retas s e t, perpendiculares a r, sendo uma
em α, e a outra em β. O ângulo θ entre s e t é, por
definição, o ângulo dos planos α e β.

18. Conceito geral de distância no
espaço
 Definição 1: se r é uma reta e P é um ponto não
pertencente a r, a distância entre P e r é a medida
do segmento PQ, sendo Q o ponto em que a
perpendicular a r, traçada por P, corta r.
P
Q
Q’
r
PQ < PQ’

19.  Definição 2: se α é um plano e A é um ponto não
pertencente a α, a distância entre A e α é a medida
do segmento AB, sendo B a projeção de A em α.
A
α
B B’
AB < AB’

20.  Bibliografia
RUBIÓ, Angel Panadés. Matemática: Ensino Médio, livro 2. Belo
Horizonte: Editora Educacional, 2012.