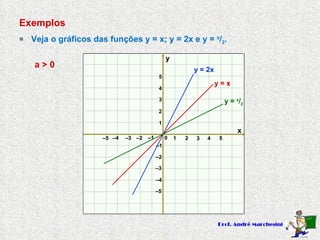
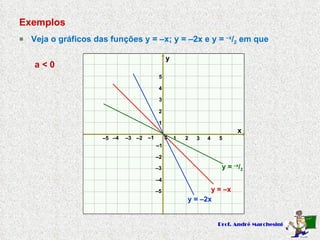
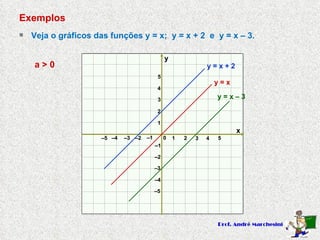
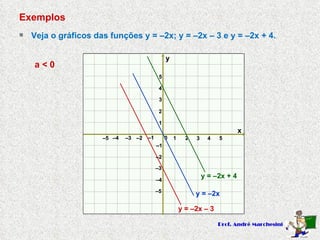
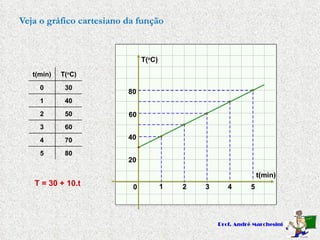
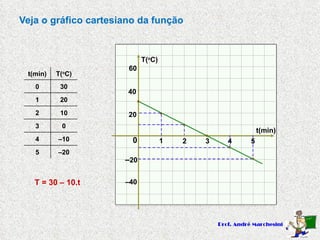
Este documento descreve funções do primeiro grau na forma y=ax+b, onde a e b são constantes. Explica que a é o coeficiente angular e determina se a função é crescente (a>0) ou decrescente (a<0), enquanto b é o coeficiente linear e representa a interseção com o eixo y. Apresenta exemplos de funções do primeiro grau e seus respectivos gráficos.

1. Representação gráfica de função 1º grau

2. Função de 1º grau é toda função do tipo y = f(x) = ax + b Em que a e b são constantes reais, com a ≠ 0 . Se b = 0 , temos a função y = f(x) = ax , chamada, também, função linear .

3. Exemplos y = f(x) = 5x – 3 é uma função de 1º grau, com a = 5 e b = –3. y = f(x) = –2x é uma função de 1º grau, com a = –2 e b = 0 Nesse caso a função é chamada de linear .

4. Características da função de 1º grau y = f(x) = ax + b . A fórmula que a define é um polinômio de 1º grau ; seu termo independente pode ser nulo ou não. Se b = 0 , temos a função f(x) = ax , chamada de função linear . A constante real a , não-nula, é o coeficiente angular . Ela é a mesma, qualquer que seja o intervalo considerado.

5. Características da função de 1º grau y = f(x) = ax + b . A constante real b é o coeficiente linear . Seu gráfico cartesiano é uma linha reta , não paralela aos eixos. Ela pode conter a origem (caso b = 0) ou não conter origem (caso b ≠ 0). O crescimento ou o decrescimento da função estão relacionados com o sinal de a . A reta é ascendente para a > 0 e descendente para a < 0 .

6. Crescimento e decrescimento. a > 0 ⇒ função crescente ⇒ reta ascendente ( sobe da esquerda p/ direita ) a < 0 ⇒ função decrescente ⇒ reta descendente ( desce da esquerda p/ direita )

7. Exemplos Veja o gráficos das funções y = x; y = 2x e y = x / 2 . x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = x y = x / 2 y = 2x a > 0

8. Exemplos Veja o gráficos das funções y = –x; y = –2x e y = –x / 2 em que x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = –x y = –x / 2 y = –2x a < 0

9. A partir do gráfico da função linear y = ax , podemos obter os gráficos de todas as funções afins y = ax + b . Deslocamos o gráfico da função y = ax para cima ou para baixo , de acordo com o valor da constante b .

10. Exemplos Veja o gráficos das funções y = x; y = x + 2 e y = x – 3. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = x a > 0 y = x – 3 y = x + 2

11. Exemplos Veja o gráficos das funções y = –2x; y = –2x – 3 e y = –2x + 4. x y 0 1 2 3 – 3 – 2 – 1 1 2 3 – 3 – 2 – 1 4 5 – 4 – 5 – 5 – 4 4 5 y = –2x + 4 y = –2x a < 0 y = –2x – 3

12. A análise das duas últimas figuras nos sugere um caso geral em relação a todas as funções afins do tipo y = f(x) = ax + b . Que relação existe entre o coeficiente b e o ponto onde cada reta corta o eixo y? b é a ordenada do ponto em que a reta corta o eixo y. Ou seja, a reta intercepta o eixo y no ponto de coordenadas (0, b).

13. Veja mais mais alguns exemplos

14. A temperatura de uma substância é 30 ºC. Sua temperatura varia com o tempo de maneira uniforme, aumentando 10 ºC por minuto. Veja as temperaturas da substância, medidas minuto a minuto. A taxa de variação da temperatura é positiva (10 o C/min). Após t minutos, a temperatura T da substância em o C é, T = 30 + 10.t t(min) 0 1 2 3 4 5 T( o C) 30 40 50 60 70 80

15. Veja o gráfico cartesiano da função t(min) T( o C) 0 1 2 3 4 20 40 60 80 5 T = 30 + 10.t t(min) T( o C) 0 30 1 40 2 50 3 60 4 70 5 80

16. A temperatura de uma substância é 30 ºC Sua temperatura varia com o tempo de maneira uniforme, diminuindo 10 ºC por minuto. Veja as temperaturas da substância, medidas minuto a minuto. A taxa de variação da temperatura é negativa (10 o C/min). Após t minutos, a temperatura T da substância em o C é, T = 30 – 10.t t(min) 0 1 2 3 4 5 T( o C) 30 20 10 0 – 10 – 20

17. Veja o gráfico cartesiano da função t(min) T( o C) 0 1 2 3 4 – 20 – 40 20 40 5 T = 30 – 10.t 60 t(min) T( o C) 0 30 1 20 2 10 3 0 4 – 10 5 – 20