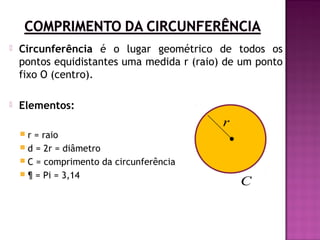
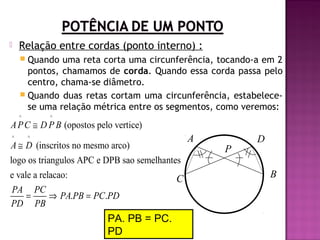
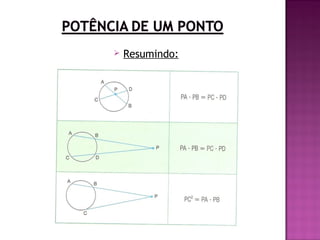
O documento apresenta os conceitos básicos de circunferência, incluindo sua definição geométrica, elementos como raio, diâmetro e comprimento, a fórmula para calcular o comprimento da circunferência e a relação entre ângulo central e comprimento do arco. Também mostra como resolver exercícios utilizando essas fórmulas e conceitos, como calcular o comprimento de um arco de 60° de uma circunferência de 21 cm de raio.

1. TC Wallace

2. 
Circunferência é o lugar geométrico de todos os
pontos equidistantes uma medida r (raio) de um ponto
fixo O (centro).

Elementos:
r
r
= raio
 d = 2r = diâmetro
 C = comprimento da circunferência
 ¶ = Pi = 3,14
C

3. 
O número ¶ é um número irracional que é
aproximado pela relação

C .
π=
d
Desta relação podemos tirar que:
C = dπ
como d = 2r
C = 2π r

Assim, o comprimento de uma circunferência é dado
pela fórmula
C = 2π r
, onde
π = 3,14
.

4. 

Arco de circunferência: é a distância entre dois
pontos pertencentes a circunferência.
O comprimento do arco é proporcional a medida do
ângulo central. Quanto maior o ângulo, maior o
comprimento do arco.
A
B
Exercício:
Qual é o comprimento de um arco de 60º de uma
circunferência de 21 cm de raio?


5. 
Exercício:
1. Qual é o comprimento de um arco de 60º de uma
circunferência de 21 cm de raio?
C = 2π r
C = 2 x3,14 x 21
C = 131,88cm
3600 = 131,88 cm
600 = x
60 x131,88
x=
360
x = 21,98 cm
A
B

6. 
Relação entre cordas (ponto interno) :
 Quando
uma reta corta uma circunferência, tocando-a em 2
pontos, chamamos de corda. Quando essa corda passa pelo
centro, chama-se diâmetro.
 Quando duas retas cortam uma circunferência, estabelecese uma relação métrica entre os segmentos, como veremos:
^
^
A P C ≅ D P B (opostos pelo vertice)
^
A
^
A ≅ D (inscritos no mesmo arco)
logo os triangulos APC e DPB sao semelhantes
e vale a relacao:
PA PC
=
⇒ PA.PB = PC.PD
PD PB
PA. PB = PC.
PD
C
P
D
B

7. Relação entre segmentos secantes (ponto exterior):

Considere os triangulos PAD e PCB :
A
C
^
P = (angulo comum)
^
^
A ≅ D (inscritos no mesmo arco)
logo os triangulos APC e DPB sao semelhantes
e vale a relacao:
PA PC
=
⇒ PA.PB = PC.PD
PD PB
PA. PB = PC.
PD
B
D
P

8. Relação entre segmentos secantes e tangente (ponto
exterior):

C
Considere os triangulos PAC e PCB :
^
P = (angulo comum)
^
P
^
A ≅ C (inscritos no mesmo arco)
logo os triangulos PAC e PCB sao semelhantes
e vale a relacao:
PA PC
=
⇒ PC 2 = PA.PB
PC PB
PC2 = PA. PB
B
A

9. 
Resumindo:

10. 
Resolução dos exercícios:
 Página
316, 317, 321 e 322.