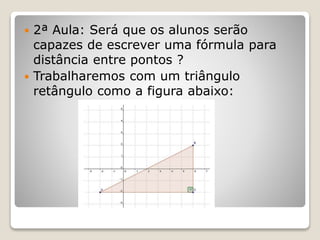
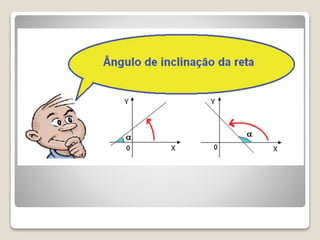
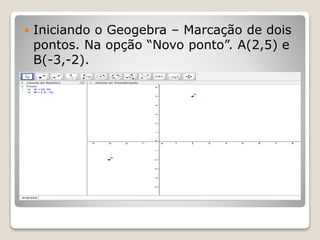
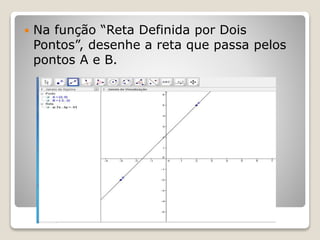
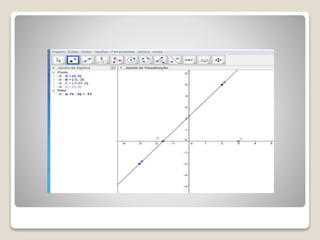
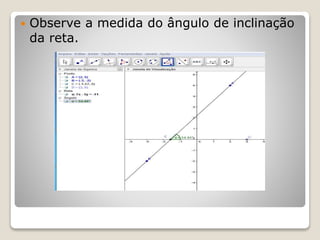
Este documento apresenta um projeto de ensino de Geometria Analítica com 8 aulas. A primeira aula revisa coordenadas cartesianas e distância entre pontos. As aulas seguintes abordam coeficiente angular, equação da reta, e uso do software Geogebra para ilustrar os conceitos. A avaliação dos alunos ocorrerá ao longo das atividades formais e informais.

1. GEOMETRIA ANALÍTICA
Informática Educativa I
Projeto de Execução
Aluno: Tânia Penner de Magalhães
Oliveira
Tutor: Luís Alberto Duncan Rangel
2014

2.  A Geometria Analítica, concebida pelo
matemático francês René Descartes
(1596-1650), que transita entre a Álgebra
e a Geometria euclidiana possibilita a
representação de figuras geométricas por
meio de pares ordenados, equações e
inequações.
Coeficiente angular e equação da reta

3.  Motivação: Os alunos farão uma pesquisa
sobre “GPS” e apresentarão o material
pesquisado para uma discussão na turma, o
objetivo é trabalhar a ideia intuitiva de
distância entre dois pontos, no caso a
distância entre o satélite e o aparelho
receptor do GPS.
 A partir dessa discussão, iniciaremos nosso
trabalho de Geometria Analítica.
 Para isso, é importante lembrar alguns
conceitos sobre o plano cartesiano ortogonal,
que consiste em um plano com dois eixos
perpendiculares, x e y, que o dividem em
quatro regiões.

4.  1ª Aula – Revisão:
 – Identifique as coordenadas dos pontos
indicados:

5.  2- Considerando como unidade de medida
o tamanho do quadrado da malha;
determine a distância entre os pares de
pontos: A e B, C e D, E e F.

6.  Para encontrar as distâncias pedidas no
item 2, o aluno deve ter contado o
número de quadrados existentes entre os
pontos, pois a medida dos lados de cada
quadrado da malha apresenta
comprimento unitário. Esse procedimento
pode ser confirmado algebricamente,
fazendo apenas a diferença entre os
valores das coordenadas que apresentam
valores diferentes.
 d(A,B) = │ 6 – 1 │= │1 – 6 │= 5

7.  2ª Aula: Será que os alunos serão
capazes de escrever uma fórmula para
distância entre pontos ?
 Trabalharemos com um triângulo
retângulo como a figura abaixo:

8.  Observe o triângulo ABC desenhado no
item anterior. Como você determinaria a
distância entre os pontos A e B? Troque
ideias com seus colegas e registre suas
conclusões.
 Esperamos que os alunos tenham
conseguido descobrir que a distância
entre dois pontos pode ser calculada
usando o Teorema de Pitágoras.
 d(A,B) = (푥푏− 푥푎)² + (푦푏 − 푦푎)2

9.  3ª e 4ª Aulas – Exercícios do livro didático
sobre coordenadas cartesianas e
distância entre dois pontos.

10.  5ª Aula – Coeficiente angular e
ângulo de inclinação:
Vamos recordar o gráfico da função
polinomial do primeiro grau, que
corresponde a uma reta. É importante
lembrar, também, do ângulo de inclinação
da reta no plano cartesiano, o qual é
definido no sentido anti-horário, a partir do
semi-eixo positivo X, como mostra a
próxima figura.

12.  Vamos assistir ao vídeo abaixo:
http://www.youtube.com/watch?v=qSTyKUd
rMZI

13.  A tangente trigonométrica do ângulo de
inclinação β (tg β) é denominada de
coeficiente angular da reta.
 Podemos obter o coeficiente angular de
uma reta a partir das coordenadas de dois
de seus pontos.

14.  6ª Aula -Vamos assistir ao vídeo abaixo:
http://www.youtube.com/watch?v=bd
wGcU3H42c

15. .Continuação do vídeo anterior:
http://www.youtube.com/watch?
v=wQ_N6Mg33Vo

16.  7ª Aula: Iremos verificar o que
aprendemos no software dinâmico
Geogebra.
 É importante lembrar que para calcular o
coeficiente angular de uma reta definida
por dois pontos, por exemplo, A(푥푎;푦푎) e
B(푥푏;푦푏), devemos usar a seguinte
expressão:
m = 푦푏- 푦푎 = variação das ordenadas
푥푏- 푥푎 variação das abscissas

17.  Iniciando o Geogebra – Marcação de dois
pontos. Na opção “Novo ponto”. A(2,5) e
B(-3,-2).

18.  Observando os pontos A e B, identifique
as suas coordenadas e calcule o
coeficiente angular da reta definida por
eles.
 m = yb - 푦푎 = -2 -5 = -7 = 1,4
푥푏 - 푥푎 -3 -2 -5

19.  Na função “Reta Definida por Dois
Pontos”, desenhe a reta que passa pelos
pontos A e B.

20.  Vamos medir o ângulo de inclinação da
reta definida pelos pontos A e B. Para
isso, você deve, primeiro, marcar dois
pontos de apoio: o ponto de interseção da
reta com o eixo X (ponto C) e outro ponto
localizado à sua direita, sobre o eixo X
(ponto D).

22.  Para medir o ângulo de inclinação,
devemos procurar pela opção “Ângulo”, e
seguir a seguinte sequência: clique no
ponto D, depois no ponto C e finalize no
ponto A.

23.  Observe a medida do ângulo de inclinação
da reta.

24.  Calcule o valor da tangente do ângulo de
inclinação, usando a calculadora do
computador.
 Você observou alguma relação existente
entre os valores encontrados para a
tangente do ângulo de inclinação e o
coeficiente angular da reta?

25.  8ª Aula – Avaliação
Os alunos serão avaliados em todas as
atividades, tanto formal como
informalmente, nas participações,
pesquisas, exercícios e envolvimento.
Faremos um blog para compartilhar o
trabalho que estamos desenvolvendo.

26.  Referências Bibliográficas:
PAIVA, Manoel. Matemática.v.3.São
Paulo: Moderna,2010
SOUZA, Joamir. Matemática.v.3. São
Paulo: FTD,2010
ROTEIROS DE AÇÂO e TEXTOS –
Geometria Analítica- Curso de Formação
Continuada – CECIERJ. Disponível
emhttp://projetoseeduc.cecierj.edu.br/ava.