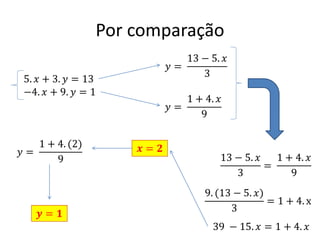
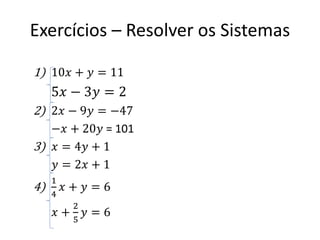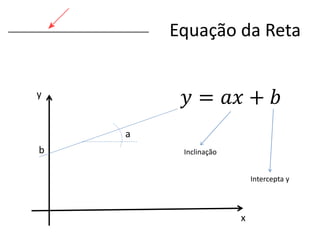
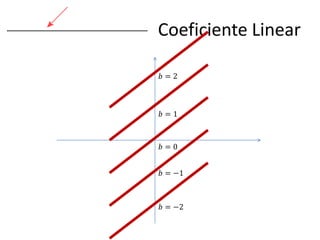
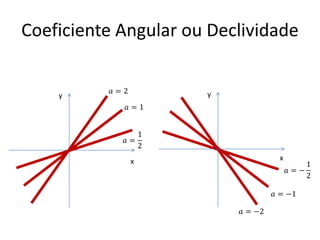
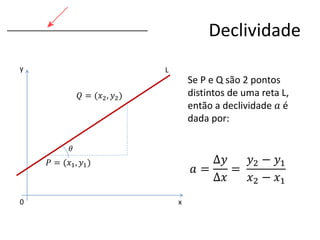
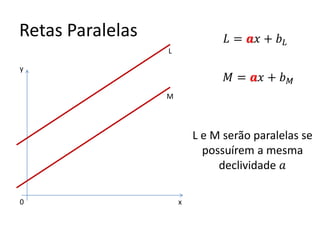
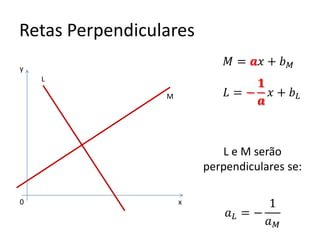
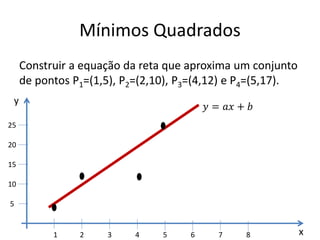
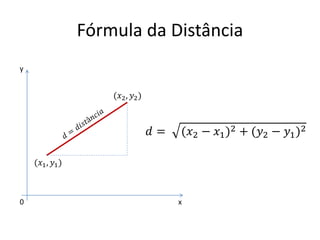
O documento apresenta conceitos básicos sobre equações de primeiro grau, incluindo: 1) A forma geral de uma equação de reta y=ax+b; 2) Como calcular a declividade e encontrar a equação de uma reta passando por um ponto com declividade dada; 3) Como representar graficamente retas e sistemas de equações de primeiro grau.

1. Unidade 6 – Equação do 1 Grau
Prof. Milton Henrique
mcouto@catolica-es.edu.br

2. Função do 1 Grau
𝑦 = 𝑎𝑥 + 𝑏
incógnita
Equação da Reta
𝟏
𝒙 = 𝒙

3. Equação da Reta
𝑦 = 𝑎𝑥 + 𝑏
y
a
b
Inclinação
Intercepta y
x

4. Exemplo – Equação da Reta
𝑦 = 5𝑥 + 2
Coeficiente Linear
Intercepta y em 2
Coeficiente Angular
Um aumento em x aumenta y em 5 unidades
𝒙
𝒚 = 𝟓𝒙 + 𝟐
0
7
2
12
3
17
4
22
y
2
1
𝑦 = 5𝑥 + 2
2
x

5. Coeficiente Linear
𝑏=2
𝑏=1
𝑏=0
𝑏 = −1
𝑏 = −2

6. Coeficiente Angular ou Declividade
y
𝑎=2
y
𝑎=1
1
𝑎=
2
x
x
1
𝑎=−
2
𝑎 = −1
𝑎 = −2

7. Declividade
y
L
Se P e Q são 2 pontos
distintos de uma reta L,
então a declividade 𝑎 é
dada por:
𝑄 = (𝑥2 , 𝑦2 )
𝜃
∆𝑦
𝑦2 − 𝑦1
𝑎=
=
∆𝑥
𝑥2 − 𝑥1
𝑃 = (𝑥1 , 𝑦1 )
0
x

8. Exemplo – Encontre a declividade da reta
que passa pelos pontos (-1,1) e (5,3)
P = (-1,1)
Q = (5,3)
∆𝑦
3−1
1
𝑎=
=
=
∆𝑥
5 − (−1)
3

9. Exercícios – Encontre a declividade da reta
que passa pelos pontos P e Q
1)
2)
3)
4)
5)
P1=(0,0) e P2=(2,4)
P1=(0,3) e P2=(8,3)
P1=(1,5;4) e P2=(2;6)
P1=(2,10) e P2=(8,1)
P1=(0,50) e P2=(8,0)

10. Equação da Reta dada um Ponto 𝑥1 , 𝑦1 e
uma declividade 𝑎
y
𝑃 = (𝑥1 , 𝑦1 )
𝜃
A equação da reta que passa pelo ponto
𝑃 = (𝑥1 , 𝑦1 ) e possui declividade 𝑎 é
dada por:
𝑦 − 𝑦1 = 𝑎. (𝑥 − 𝑥1 )
0
x

11. Exemplo – Encontre a equação da reta que
passa pelo ponto (1,3) e tem declividade 2
𝑦 − 𝑦1 = 𝑎. (𝑥 − 𝑥1 )
𝑦 − 3 = 2. (𝑥 − 1)
𝑦 = 2. 𝑥 − 1 + 3
𝑦 = 2𝑥 − 2 + 3
𝑦 = 2𝑥 + 1

12. Exercícios – Encontre a equação da reta que
passa pelo ponto P e possui declividade a
1)
2)
3)
4)
5)
P = (4,7) e a=3
P = (-3,2) e a=1
P = (4,-1) e a=-2
P = (1,-4) e a=0,5
P = (-2,-5) e a=-0,3

13. Retas Paralelas
𝐿 = 𝒂𝑥 + 𝑏 𝐿
L
y
𝑀 = 𝒂𝑥 + 𝑏 𝑀
M
L e M serão paralelas se
possuírem a mesma
declividade 𝑎
0
x

14. Retas Perpendiculares
𝑀 = 𝒂𝑥 + 𝑏 𝑀
y
L
𝟏
𝐿 = − 𝑥 + 𝑏𝐿
𝒂
M
L e M serão
perpendiculares se:
0
x
1
𝑎𝐿 = −
𝑎𝑀

15. Exercícios – Represente Graficamente
1)
2)
3)
4)
𝑦 = 2𝑥 − 4, 𝑥 ∈ 0,5
𝑦 = 6, −2 ≤ 𝑥 ≤ 3
𝑦 = 10 − 2𝑥, 𝑥 ∈ 0,5
𝑦 = 4𝑥
5) 𝑦 =
1
3
𝑥
3
+
4

16. Exemplo
Calcule a Equação da Reta que passa pelos pontos
P1=(1,3) e P2=(3,7)
Equação da Reta → 𝑦 = 𝑎𝑥 + 𝑏
𝑃1 = 𝑥1 = 1, 𝑦1 = 3
3 = 1𝑎 + 𝑏
𝑃2 = 𝑥2 = 3, 𝑦2 = 7
7 = 3𝑎 + 𝑏
Resolvendo o sistema:
𝒚 = 𝟐𝒙 + 𝟏
𝒂= 𝟐
𝒃= 𝟏

17. Exercícios – Escreva a Equação da Reta
1)
2)
3)
4)
5)
P1=(0,0) e P2=(2,4)
P1=(0,3) e P2=(8,3)
P1=(1,5;4) e P2=(2;6)
P1=(2,10) e P2=(8,1)
P1=(0,50) e P2=(8,0)

18. Mínimos Quadrados
Construir a equação da reta que aproxima um conjunto
de pontos P1=(1,5), P2=(2,10), P3=(4,12) e P4=(5,17).
y
𝑦 = 𝑎𝑥 + 𝑏
25
20
15
10
5
1
2
3
4
5
6
7
8
x

19. Mínimos Quadrados
x
y
x.y
x2
P1
1
5
5
1
P2
2
10
20
4
P3
4
12
48
16
P4
5
17
85
25
Soma
12
44
158
46
Média
3
11
39,5
11,5
𝑦 = 𝑎𝑥 + 𝑏
158 − 4.3.11
𝑎=
46 − 4(3)2
𝑏 = 11 − 2,6.3
𝑎=
𝑥𝑦 − 𝑛 𝑥 𝑦
𝑥 2 − 𝑛( 𝑥)2
𝑏= 𝑦− 𝑎𝑥
𝒂 = 𝟐, 𝟔
𝐲 = 𝟐, 𝟔𝐱 + 𝟑, 𝟐
𝒃 = 𝟑, 𝟐

20. Exercícios – Mínimos Quadrados
1)
2)
3)
4)
P1=(0,0), P2=(2,5), P3=(3,8) e P4=(4,9)
P1=(-1,0), P2=(0,2), P3=(1,3), P4=(2,6) e P5=(3,5)
P1=(0,20), P2=(2,12), P3=(4,7), P4=(6,3) e P5=(8;0,5)
P1=(1,20), P2=(5,40), P3=(10,70) e P4=(15,90)

21. Fórmula da Distância
y
(𝑥2 , 𝑦2 )
𝑑=
(𝑥2 − 𝑥1 )2 + (𝑦2 − 𝑦1 )2
(𝑥1 , 𝑦1 )
0
x

22. Exemplo – Fórmula da Distância
Encontre a distância entre os pontos (-4,3) e (2,6)
𝑑=
(𝑥2 − 𝑥1 )2 + (𝑦2 − 𝑦1 )2
𝑑=
(2 −(−4))2 +(6 − 3)2
𝑑=
(6)2 + (3)2
𝑑=
45

23. Exercícios – Encontre a Distância entre P e Q
1)
2)
3)
4)
5)
P=(1,3) e Q=(4,7)
P=(-1,3) e Q=(4,9)
P=(0,2) e Q=(9,7)
P=(-5,-3) e Q=(-4,-8)
P=(-9,3) e Q=(-4,7)

24. Sistema de Equações do 1º Grau
Forma Geral
𝐴. 𝑥 + 𝐵. 𝑦 = 𝐶
𝐴′. 𝑥 + 𝐵′. 𝑦 = 𝐶′
Exemplo
5. 𝑥 + 3. 𝑦 = 13
−4. 𝑥 + 9. 𝑦 = 1
3 Formas de Resolução
• Por adição
• Por comparação
• Por substituição

25. Por adição
5. 𝑥 + 3. 𝑦 = 13
−4. 𝑥 + 9. 𝑦 = 1
Multiplicando-se a 1ª equação por (-3)
−15. 𝑥 − 9. 𝑦 = −39 Somando membro a membro as 2 equações
−4. 𝑥 + 9. 𝑦 = 1
−19. 𝑥 = −38
Fazendo x = 2 na 2ª equação, temos
𝒙= 𝟐
−4. (2) + 9. 𝑦 = 1
9. 𝑦 = 9
𝒚= 𝟏

26. Por comparação
13 − 5. 𝑥
𝑦=
3
5. 𝑥 + 3. 𝑦 = 13
−4. 𝑥 + 9. 𝑦 = 1
1 + 4. (2)
𝑦=
9
𝒚= 𝟏
1 + 4. 𝑥
𝑦=
9
𝒙= 𝟐
13 − 5. 𝑥
1 + 4. 𝑥
=
3
9
9. (13 − 5. 𝑥)
= 1 + 4. x
3
39 − 15. 𝑥 = 1 + 4. 𝑥

27. Por substituição
5. 𝑥 + 3. 𝑦 = 13
−4. 𝑥 + 9. 𝑦 = 1
13 − 5. 𝑥
𝑦=
3
Substituindo o valor de y na 2ª equação
13 − 5. 𝑥
−4. 𝑥 + 9.
=1
3
𝒙= 𝟐
Substituindo o valor de x na equação
13 − 5. (2)
𝑦=
3
𝒚= 𝟏

28. Exercícios – Resolver os Sistemas
1) 10𝑥 + 𝑦 = 11
5𝑥 − 3𝑦 = 2
2) 2𝑥 − 9𝑦 = −47
−𝑥 + 20𝑦 = 101
3) 𝑥 = 4𝑦 + 1
𝑦 = 2𝑥 + 1
4)
1
4
𝑥+ 𝑦=6
𝑥+
2
5
𝑦=6

29. Quem sou eu?
Prof. Milton Henrique do Couto Neto
mcouto@catolica-es.edu.br
Engenheiro Mecânico, UFF
MBA em Gestão Empresarial, UVV
MBA em Marketing Empresarial, UVV
Mestre em Administração, UFES
Pós-MBA em Inteligência Empresarial, FGV
http://lattes.cnpq.br/8394911895758599

30. Professor Universitário
2004
2011
2006
2007
2009
2011

31. Disciplinas
Lecionadas
Marketing
Empreendedorismo
Administração de Materiais
Matemática
Matemática Financeira
Gestão Financeira
Fundamentos da Administração
Gestão de Processos e Empresas

32. miltonhenrique
miltonhcouto
miltonhcouto

33. Este e outros arquivos estão
disponíveis para download no
www.slideshare.net/miltonh