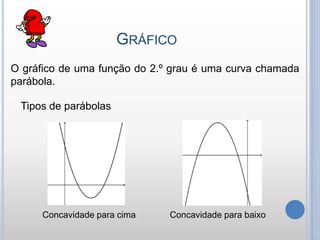
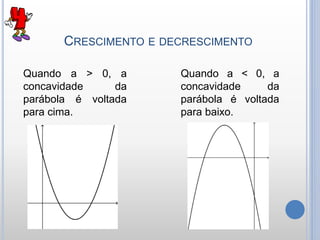
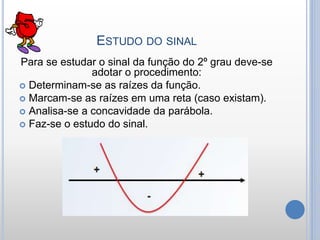
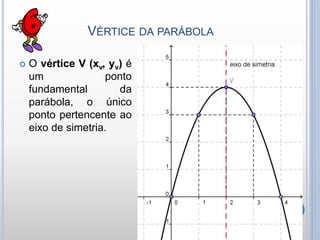
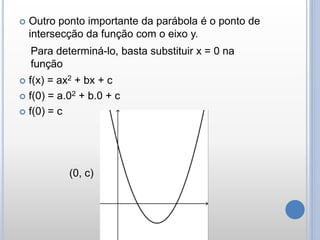
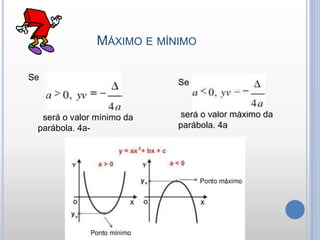
O documento descreve as características e propriedades das funções quadráticas. Uma função quadrática é definida como f(x) = ax2 + bx + c, onde a, b e c são números reais e a ≠ 0. O gráfico de uma função quadrática é uma parábola, que pode ter concavidade para cima ou para baixo. As raízes de uma função quadrática podem ser encontradas usando a fórmula de Bhaskara, e dependem do sinal do discriminante ∆.

1. FUNÇÃO QUADRÁTICA
Pausa Matemática

2. CONCEITO
Chama-se FUNÇÃO POLINOMIAL DO 2º GRAU ou
FUNÇÃO QUADRÁTICA qualquer função de R em R
dada por uma lei da forma:
f(x) = ax2 + bx + c
onde a, b e c são números reais e a ≠ 0.
Identificação de coeficientes da função quadrática:
2x2 - 3x + 5 = 0
a = 2
b = -3
c = 5
4x + 8x2 - 4 = 0
a = 8
b = 4
c = -4

3. GRÁFICO
O gráfico de uma função do 2.º grau é uma curva chamada
parábola.
Tipos de parábolas
Concavidade para cima Concavidade para baixo

4. RAIZ (ZERO) DA FUNÇÃO QUADRÁTICA
 Para determinar as raízes (ou zeros) da função do 2º
grau f(x) = ax2 + bx + c, basta calcular os valores de x
que tem imagem igual a zero.
Ou seja, devemos resolver a equação do 2º grau
ax2 + bx + c = 0.
E, para isso, usamos a fórmula de báskara.
2a
Δb
x


Podemos estabelecer uma relação entre o
discriminante ∆ e a intersecção da parábola com o
eixo x.

5.  Se ∆ > 0, a função tem duas raízes reais e a
parábola intercepta o eixo x em dois pontos.
 Se ∆ = 0, a função tem duas raízes reais iguais e a
parábola intercepta o eixo x em um único ponto.
 Se ∆ < 0, a função não tem raízes reais e a
parábola não intercepta o eixo x.
ou
ou
ou

6. CRESCIMENTO E DECRESCIMENTO
Quando a > 0, a
concavidade da
parábola é voltada
para cima.
Quando a < 0, a
concavidade da
parábola é voltada
para baixo.

7. ESTUDO DO SINAL
Para se estudar o sinal da função do 2º grau deve-se
adotar o procedimento:
 Determinam-se as raízes da função.
 Marcam-se as raízes em uma reta (caso existam).
 Analisa-se a concavidade da parábola.
 Faz-se o estudo do sinal.

8. VÉRTICE DA PARÁBOLA
 O vértice V (xv, yv) é
um ponto
fundamental da
parábola, o único
ponto pertencente ao
eixo de simetria.

9.  Para determinar o vértice da parábola, fazemos o
seguinte:
Calculamos a média aritmética das raízes x’ e x’’, para
obtermos a abscissa (xv) desse vértice.
Em seguida, substituímos xv, na função e encontramos
a ordenada do vértice yv.
Outra maneira de obter o vértice V (xv, yv) de uma
parábola da equação f(x) = ax2 + bx + c, é:
2
'x'x'
xv


2a
b
xv 
4a
Δ
yv 

10.  Outro ponto importante da parábola é o ponto de
intersecção da função com o eixo y.
 f(x) = ax2 + bx + c
 f(0) = a.02 + b.0 + c
 f(0) = c
(0, c)
Para determiná-lo, basta substituir x = 0 na
função

11. MÁXIMO E MÍNIMO
Se
será o valor mínimo da
parábola. 4a-
Se
será o valor máximo da
parábola. 4a