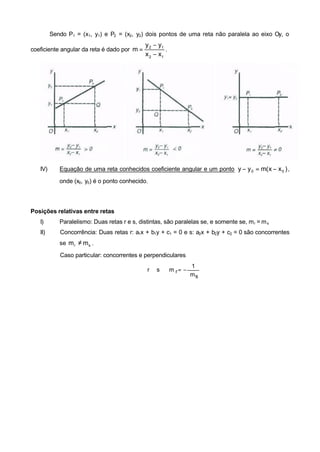
O documento descreve os conceitos fundamentais da Geometria Analítica, incluindo o sistema cartesiano de eixos, quadrantes, distância entre pontos, ponto médio, alinhamento de pontos, equações de retas e posições relativas entre retas. Exemplos e exercícios ilustram a aplicação destes conceitos.

1. GEOMETRIA ANALÍTICA
A Geometria Analítica teve como principal idealizador o francês René Descartes (1596 – 1650).
Com o auxílio de um sistema de eixos associados a um plano, faz-se corresponder a cada ponto
do plano um par ordenado e vice-versa.
Quando os eixos desse sistema são perpendiculares entre si, em um ponto O (origem), essa
correspondência determina um sistema cartesiano ortogonal (ou plano cartesiano).
y
2º quadrante 1º quadrante
x
O
4º quadrante
3º quadrante
1º quadrante: x>0 e y>0
2º quadrante: x<0 e y>0
3º quadrante: x<0 e y<0
4º quadrante: x>0 e y<0
Distância de dois pontos
Dados os pontos A = (xA, yA) e B = (xB, yB), calcula-se a distância entre eles, aplicando o teorema
de Pitágoras no triângulo ABC,
seja d a distância entre os pontos A e B

2. d2 = (AC)2 + (BC)2
d2 = (xB – xA)2 + (yB – yA)2 B
d= ( x B − x A )2 + ( y B − y A ) 2
Ponto médio
Dados os pontos A = (xA, yA), B = (xB, y B) e P que divide AB ao meio, temos:
 xA + xB y A + yB 
P=  , 
 2 2 
Condição de alinhamento de três pontos
Se três pontos A = (xA, yA), B = (xB , yB) e C = (xC , yC ) estão alinhados, então:
xA yA 1
xB yB 1 = 0
xC yC 1
Equações de uma reta
I) Equação geral é obtida a partir da condição de alinhamento de três pontos. A toda reta
r do plano cartesiano está associada ao menos uma equação da forma ax + by + c = 0
onde a, b, c são números reais, a ≠ 0 ou b ≠ 0 e (x,y) representa um ponto genérico da
reta r.
II) Equações paramétricas são equações da forma x = f(t) e y = f(t), que relacionam as
coordenadas x e y dos pontos da reta com um parâmetro “t”.
III) Equação reduzida é obtida isolando-se o y na equação geral ax + by + c = 0, onde
a c a c
obtemos y = − x − . Fazendo-se − = m e − = q , temos y = mx + q.
b b b b
m é chamado de coeficiente angular da reta r, ( fornece a inclinação da reta em relação ao
 π
eixo Ox, m = tg θ  θ ≠ 
 2
q é chamado coeficiente linear ( é a ordenada do ponto em que a reta intercepta Oy)

3. Sendo P1 = (x1, y1) e P2 = (x2, y2) dois pontos de uma reta não paralela ao eixo Oy, o
y 2 − y1
coeficiente angular da reta é dado por m = .
x 2 − x1
IV) Equação de uma reta conhecidos coeficiente angular e um ponto y − y 0 = m( x − x 0 ) ,
onde (x0, y0) é o ponto conhecido.
Posições relativas entre retas
I) Paralelismo: Duas retas r e s, distintas, são paralelas se, e somente se, m r = m s
II) Concorrência: Duas retas r: a1x + b1y + c1 = 0 e s: a2x + b2y + c2 = 0 são concorrentes
se m r ≠ m s .
Caso particular: concorrentes e perpendiculares
1
r ⊥ s ⇔ m r= −
ms

4. EXERCÍCIOS SOBRE GEOMETRIA ANALÍTICA
1) Os pontos A = (-4, -2) e B = (-2, 2) pertencem respectivamente aos quadrantes:
a) 1º e 2º
b) 2º e 3º
c) 3º e 2º
d) 4º e 2º
e) 3º e 4º
2) O ponto A = (m+3, n-1) pertence ao 3º quadrante, para os possíveis valores de m e n:
a) m > 3 e n < 1
b) m < 3 e n > 1
c) m < -3 e n > 1
d) m < -3 e n < -1
e) m < -3 e n < 1
3) Num triângulo ABC, sendo A = (4,3), B = (0,3) e C um ponto pertencente ao eixo Ox com
AC = BC. O ponto C tem como coordenadas:
a) (2,0)
b) (-2,0)
c) (0,2)
d) (0,-2)
e) (2,-2)
4) A distância entre os pontos P = (1,0) e Q = (2, 8 ) é:
a) 7
b) 3
c) 2
d) 2 7
e) 5
5) O valor de x para que os pontos A = (x, 5), B = (-2,3) e C = (4,1) sejam alinhados é:
a) 8
b) 6
c) -5
d) -8
e) 7

5. 6) Os pontos A = (0,0), B = (3,7) e C = (5, -1) são vértices de um triângulo. O comprimento da
mediana AM é:
a) 3
b) 4
c) 5
d) 6
e) 7
7) O coeficiente angular da reta que passa pelos pontos A = (-1,2) e B = (3,6) é:
a) -1
1
b)
2
2
c)
3
d) 3
e) 1
8) A equação da reta que passa pelo ponto (-1,-2) e tem coeficiente angular -1 é:
a) x + y -1 = 0
b) x + y +1 = 0
c) x + y -3 = 0
d) x + y +3 = 0
e) x – y + 3 = 0
9) equação da reta que passa pelos pontos (2, -3) e (8, 1) é:
a) 2x – 3y – 13 = 0
b) -2x – 3y + 13 = 0
c) 3x – 2y + 13 = 0
d) 2x – 3y + 13 = 0
e) 2x + 3y – 13 = 0
10) O ponto de interseção das retas x + 2y = 3 e 2x + 3y – 5 = 0 é:
a) (1,-1)
b) (1,1)
c) (1,2)
d) (-1,1)
e) (2,1)

6. 11) O valor de “a” para que as retas r: ax + y – 4 = 0 e s: 3x + 3y – 7 = 0 sejam paralelas é:
a) 1
1
b)
2
c) 2
d) 3
e) -1
RESPOSTAS DOS EXERCÍCIOS SOBRE GEOMETRIA ANALÍTICA
1) c
2) e
3) a
4) b
5) d
6) c
7) e
8) d
9) a
10) b
11) a