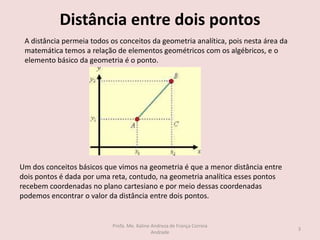
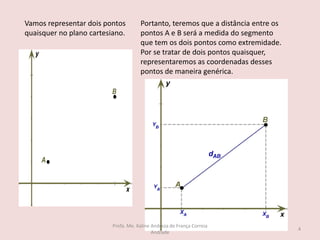
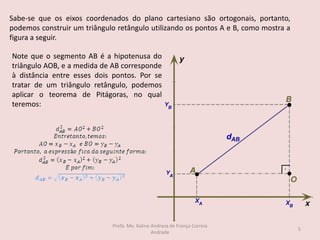
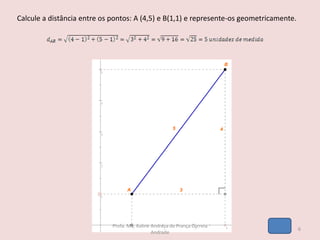
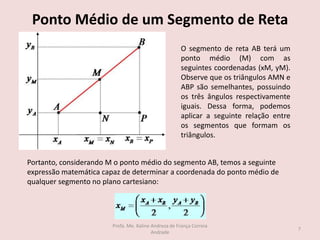
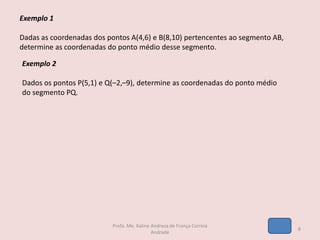
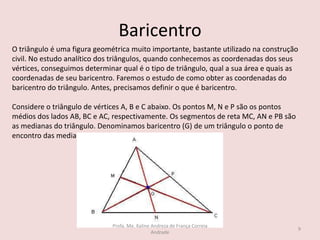
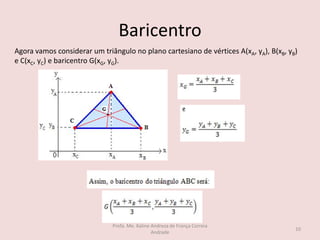
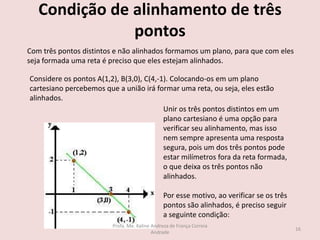
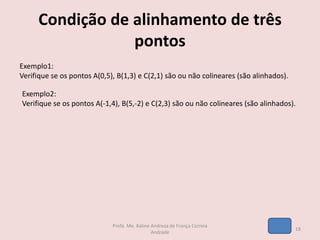
O documento discute os seguintes tópicos de geometria analítica: 1) cálculo da distância entre dois pontos no plano cartesiano, 2) determinação das coordenadas do ponto médio de um segmento, 3) cálculo das coordenadas do baricentro de um triângulo, 4) fórmula para calcular a área de um triângulo a partir das coordenadas de seus vértices, e 5) condição matemática para que três pontos estejam alinhados.

1. GEOMETRIA ANALÍTICA
Distância entre dois pontos
Ponto Médio
Baricentro
Área de um triângulo qualquer
Condição de alinhamento de três pontos
Ponto e Reta
1Profa. Me. Kaline Andreza de França Correia Andrade

2. Introdução
• A Geometria Analítica, também denominada de coordenadas geométricas, se baseia nos
estudos da Geometria através da utilização da Álgebra. Os estudos iniciais estão ligados ao
matemático francês René Descartes (1596 -1650), criador do sistema de coordenadas
cartesianas.
Os estudos relacionados à Geometria Analítica datam seu início no século XVII, Descartes, ao
relacionar a Álgebra com a Geometria, criou princípios matemáticos capazes de analisar por
métodos geométricos as propriedades do ponto, da reta e da circunferência, determinando
distâncias entre eles, localização e pontos de coordenadas.
• Os cientistas Isaac Newton e Gottfried Wilhelm Leibniz concentraram estudos na Geometria
Analítica, que serviu como base teórica e prática para o surgimento do Cálculo Diferencial e
Integral, muito utilizado atualmente na Engenharia.
2
Profa. Me. Kaline Andreza de França Correia
Andrade

3. Distância entre dois pontos
A distância permeia todos os conceitos da geometria analítica, pois nesta área da
matemática temos a relação de elementos geométricos com os algébricos, e o
elemento básico da geometria é o ponto.
Um dos conceitos básicos que vimos na geometria é que a menor distância entre
dois pontos é dada por uma reta, contudo, na geometria analítica esses pontos
recebem coordenadas no plano cartesiano e por meio dessas coordenadas
podemos encontrar o valor da distância entre dois pontos.
3
Profa. Me. Kaline Andreza de França Correia
Andrade

4. Vamos representar dois pontos
quaisquer no plano cartesiano.
Portanto, teremos que a distância entre os
pontos A e B será a medida do segmento
que tem os dois pontos como extremidade.
Por se tratar de dois pontos quaisquer,
representaremos as coordenadas desses
pontos de maneira genérica.
4
Profa. Me. Kaline Andreza de França Correia
Andrade

5. Sabe-se que os eixos coordenados do plano cartesiano são ortogonais, portanto,
podemos construir um triângulo retângulo utilizando os pontos A e B, como mostra a
figura a seguir.
Note que o segmento AB é a hipotenusa do
triângulo AOB, e a medida de AB corresponde
à distância entre esses dois pontos. Por se
tratar de um triângulo retângulo, podemos
aplicar o teorema de Pitágoras, no qual
teremos:
5
Profa. Me. Kaline Andreza de França Correia
Andrade

6. Calcule a distância entre os pontos: A (4,5) e B(1,1) e represente-os geometricamente.
6
Profa. Me. Kaline Andreza de França Correia
Andrade

7. Ponto Médio de um Segmento de Reta
O segmento de reta AB terá um
ponto médio (M) com as
seguintes coordenadas (xM, yM).
Observe que os triângulos AMN e
ABP são semelhantes, possuindo
os três ângulos respectivamente
iguais. Dessa forma, podemos
aplicar a seguinte relação entre
os segmentos que formam os
triângulos.
Portanto, considerando M o ponto médio do segmento AB, temos a seguinte
expressão matemática capaz de determinar a coordenada do ponto médio de
qualquer segmento no plano cartesiano:
7
Profa. Me. Kaline Andreza de França Correia
Andrade

8. Exemplo 1
Dadas as coordenadas dos pontos A(4,6) e B(8,10) pertencentes ao segmento AB,
determine as coordenadas do ponto médio desse segmento.
Exemplo 2
Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio
do segmento PQ.
8
Profa. Me. Kaline Andreza de França Correia
Andrade

9. Baricentro
O triângulo é uma figura geométrica muito importante, bastante utilizado na construção
civil. No estudo analítico dos triângulos, quando conhecemos as coordenadas dos seus
vértices, conseguimos determinar qual é o tipo de triângulo, qual a sua área e quais as
coordenadas de seu baricentro. Faremos o estudo de como obter as coordenadas do
baricentro do triângulo. Antes, precisamos definir o que é baricentro.
Considere o triângulo de vértices A, B e C abaixo. Os pontos M, N e P são os pontos
médios dos lados AB, BC e AC, respectivamente. Os segmentos de reta MC, AN e PB são
as medianas do triângulo. Denominamos baricentro (G) de um triângulo o ponto de
encontro das medianas.
9
Profa. Me. Kaline Andreza de França Correia
Andrade

10. Baricentro
Agora vamos considerar um triângulo no plano cartesiano de vértices A(xA, yA), B(xB, yB)
e C(xC, yC) e baricentro G(xG, yG).
10
Profa. Me. Kaline Andreza de França Correia
Andrade

11. Baricentro
Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7),
B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente,
para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
11
Profa. Me. Kaline Andreza de França Correia
Andrade

12. Área de um Triângulo
na Geometria Analítica
Vamos determinar a área de um triângulo do ponto de vista da geometria analítica.
Assim, considere três pontos quaisquer, não colineares, A (xa, ya), B (xb, yb) e C (xc, yc).
Como esses pontos não são colineares, ou seja, não estão numa mesma reta, eles
determinam um triângulo. A área desse triângulo será dada por:
Observe que a área será metade do módulo do determinante das
coordenadas dos pontos A, B e C.
12
Profa. Me. Kaline Andreza de França Correia
Andrade

13. Área de um Triângulo
na Geometria Analítica
Exemplo 1. Calcule a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6).
Solução: Primeiro passo é fazer o cálculo do determinante das coordenadas dos
pontos A, B e C.
Portanto, a área do triângulo de vértices A (4 , 0), B (0 , 0) e C (0 , 6) é 12.
13
Profa. Me. Kaline Andreza de França Correia
Andrade

14. Área de um Triângulo
na Geometria Analítica
Exemplo 2. Determine a área do triângulo de vértices A (1, 3), B (2, 5) e C (-2,4).
Solução: Primeiro devemos realizar o cálculo do determinante.
14
Profa. Me. Kaline Andreza de França Correia
Andrade

15. Área de um Triângulo
na Geometria Analítica
Exemplo 3. Os pontos A (0, 0), B (0, -8) e C (x, 0) determinam um triângulo de área
igual a 20. Encontre o valor de x.
Solução: Sabemos que a área do triângulo de vértices A, B e C é 20. Então:
15
Profa. Me. Kaline Andreza de França Correia
Andrade

16. Condição de alinhamento de três
pontos
Com três pontos distintos e não alinhados formamos um plano, para que com eles
seja formada uma reta é preciso que eles estejam alinhados.
Considere os pontos A(1,2), B(3,0), C(4,-1). Colocando-os em um plano
cartesiano percebemos que a união irá formar uma reta, ou seja, eles estão
alinhados.
Unir os três pontos distintos em um
plano cartesiano é uma opção para
verificar seu alinhamento, mas isso
nem sempre apresenta uma resposta
segura, pois um dos três pontos pode
estar milímetros fora da reta formada,
o que deixa os três pontos não
alinhados.
Por esse motivo, ao verificar se os três
pontos são alinhados, é preciso seguir
a seguinte condição:
16
Profa. Me. Kaline Andreza de França Correia
Andrade

17. Condição de alinhamento de três
pontos
Três pontos não alinhados em um plano cartesiano formam um triângulo de
vértices A(xA, yA), B(xB, yB) e C(xC, yC). A sua área poderá ser calculada da
seguinte forma:
Para que exista a área do triângulo esse determinante deverá ser diferente de
zero. Caso seja igual a zero os três pontos, que eram os vértices do triângulo, só
poderão estar alinhados.
Portanto, podemos concluir que três pontos distintos A(xA, yA), B(xB, yB) e C(xC, yC)
estarão alinhados se
= 0
17
Profa. Me. Kaline Andreza de França Correia
Andrade

18. Condição de alinhamento de três
pontos
Exemplo1:
Verifique se os pontos A(0,5), B(1,3) e C(2,1) são ou não colineares (são alinhados).
Exemplo2:
Verifique se os pontos A(-1,4), B(5,-2) e C(2,3) são ou não colineares (são alinhados).
18
Profa. Me. Kaline Andreza de França Correia
Andrade