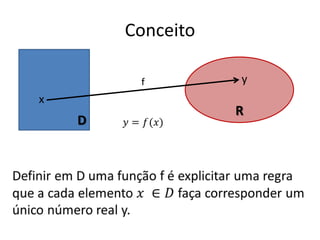
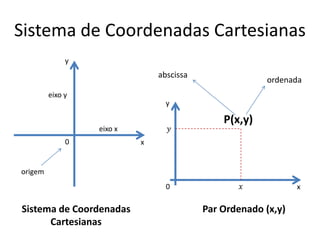
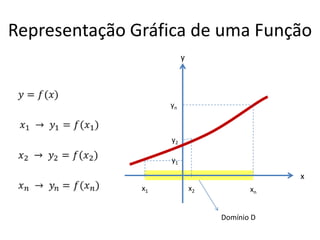
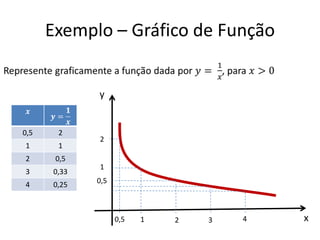
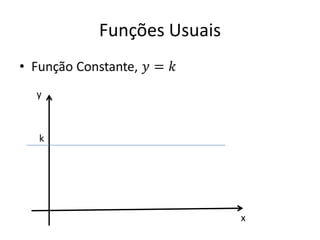
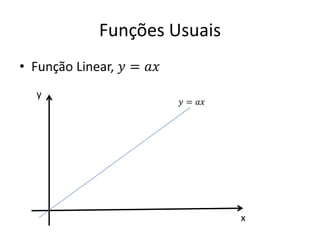
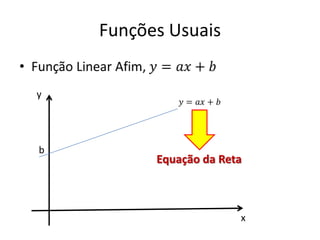
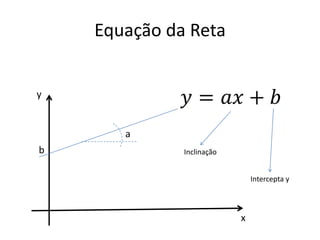
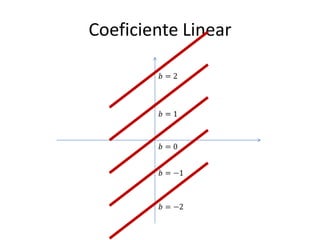
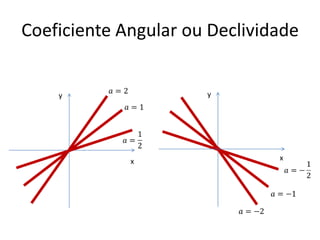
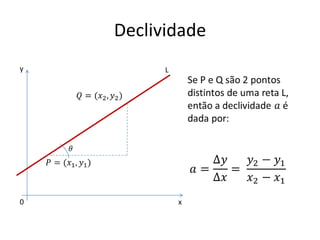
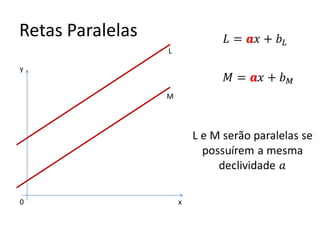
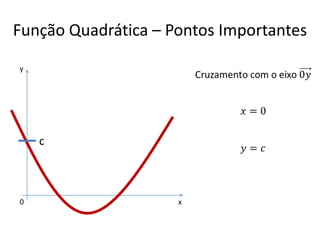
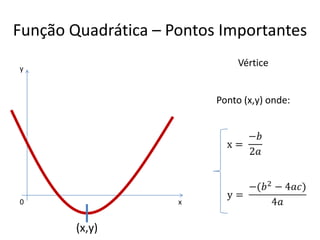
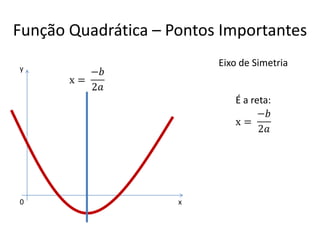
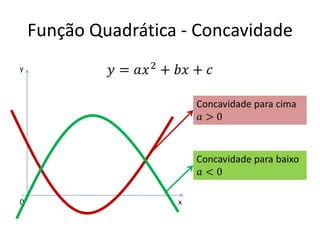
O documento aborda conceitos fundamentais de funções, incluindo igualdade, operações, e representação gráfica no sistema de coordenadas cartesianas. Além disso, discute equações da reta, coeficientes, mínimos quadrados e distância entre pontos, culminando em uma introdução às funções quadráticas. Exemplos e exercícios são fornecidos para facilitar a compreensão dos tópicos abordados.

1. Unidade 5 - Funções
Prof. Milton Henrique
mcouto@catolica-es.edu.br

2. Conteúdo
• Conceito
• Igualdade de Funções
• Operações com Funções
• Sistema de Coordenadas Cartesianas
• Representação Gráfica de Função
• Funções Usuais
• Equação da Reta
• Coeficiente Linear e Angular (Declividade)
• Mínimos Quadrados
• Distância entre dois pontos
• Função Quadrática

3. Conceito
D
R
x
yf

4. Conceito – Exemplo

5. Igualdade de Funções
f e g são iguais quando
Df = Dg

6. Operações com Funções - Soma

7. Operações com Funções - Produto

8. Operações com Funções - Quociente

9. Sistema de Coordenadas Cartesianas
x
x
y
y
eixo x
eixo y
origem
0
0
P(x,y)
Par Ordenado (x,y)Sistema de Coordenadas
Cartesianas
abscissa
ordenada

10. Representação Gráfica de uma Função
x
y
x1 x2 xn
yn
y2
y1
Domínio D

11. Exemplo – Gráfico de Função
0,5 2
1 1
2 0,5
3 0,33
4 0,25
x
y
0,5 1 2 3 4
1
2
0,5

12. Exercícios – Represente Graficamente

13. Funções Usuais
x
y
k

14. Funções Usuais
x
y

15. Funções Usuais
x
y
b
Equação da Reta

16. Equação da Reta
x
y
b
a
Inclinação
Intercepta y

17. Exemplo – Equação da Reta
Coeficiente Linear
Intercepta y em 2
Coeficiente Angular
Um aumento em x aumenta y em 5 unidades
0 2
1 7
2 12
3 17
4 22
x
y
2

18. Coeficiente Linear

19. Coeficiente Angular ou Declividade
x
y
x
y

20. Declividade
0 x
y L

21. Exemplo – Encontre a declividade da reta
que passa pelos pontos (-1,1) e (5,3)
Q = (5,3)
P = (-1,1)

22. Exercícios – Encontre a declividade da reta
que passa pelos pontos P e Q
1) P1=(0,0) e P2=(2,4)
2) P1=(0,3) e P2=(8,3)
3) P1=(1,5;4) e P2=(2;6)
4) P1=(2,10) e P2=(8,1)
5) P1=(0,50) e P2=(8,0)

23. 0 x
y

24. Exemplo – Encontre a equação da reta que
passa pelo ponto (1,3) e tem declividade 2

25. Exercícios – Encontre a equação da reta que
passa pelo ponto P e possui declividade a
1) P = (4,7) e a=3
2) P = (-3,2) e a=1
3) P = (4,-1) e a=-2
4) P = (1,-4) e a=0,5
5) P = (-2,-5) e a=-0,3

26. Retas Paralelas
0 x
y
L
M

27. Retas Perpendiculares
0 x
y
L
M
L e M serão
perpendiculares se:

28. Exercícios – Represente Graficamente

29. Exemplo
Calcule a Equação da Reta que passa pelos pontos
P1=(1,3) e P2=(3,7)
Resolvendo o sistema:

30. Exercícios – Escreva a Equação da Reta
1) P1=(0,0) e P2=(2,4)
2) P1=(0,3) e P2=(8,3)
3) P1=(1,5;4) e P2=(2;6)
4) P1=(2,10) e P2=(8,1)
5) P1=(0,50) e P2=(8,0)

31. Mínimos Quadrados
Construir a equação da reta que aproxima um conjunto
de pontos P1=(1,5), P2=(2,10), P3=(4,12) e P4=(5,17).
x
y
1 2 3 4 5 6 7 8
5
10
15
20
25

32. Mínimos Quadrados
x y x.y x2
P1 1 5 5 1
P2 2 10 20 4
P3 4 12 48 16
P4 5 17 85 25
Soma 12 44 158 46
Média 3 11 39,5 11,5

33. Exercícios – Mínimos Quadrados
1) P1=(0,0), P2=(2,5), P3=(3,8) e P4=(4,9)
2) P1=(-1,0), P2=(0,2), P3=(1,3), P4=(2,6) e P5=(3,5)
3) P1=(0,20), P2=(2,12), P3=(4,7), P4=(6,3) e P5=(8;0,5)
4) P1=(1,20), P2=(5,40), P3=(10,70) e P4=(15,90)

34. Fórmula da Distância
0 x
y

35. Exemplo – Fórmula da Distância
Encontre a distância entre os pontos (-4,3) e (2,6)

36. Exercícios – Encontre a Distância entre P e Q
1) P=(1,3) e Q=(4,7)
2) P=(-1,3) e Q=(4,9)
3) P=(0,2) e Q=(9,7)
4) P=(-5,-3) e Q=(-4,-8)
5) P=(-9,3) e Q=(-4,7)

37. Função Quadrática
0 x
y
Parábola

38. Função Quadrática – Pontos Importantes
0 x
y
x1 x2

39. Função Quadrática – Pontos Importantes
0 x
y
c

40. Função Quadrática – Pontos Importantes
0 x
y
Vértice
(x,y)
Ponto (x,y) onde:

41. Função Quadrática – Pontos Importantes
0 x
y
Eixo de Simetria
É a reta:

42. Função Quadrática - Concavidade
0 x
y

43. X1= 2 X2= 4
Vértice
Eixo de Simetria
X= 3 y= -1
X= 3
Concavidade
Concavidade para cima

44. Continuação do Exemplo
0 x
y
8
(3,-1)
2 4
X=3
Concavidade
para cima

45. Exercícios – Construir a Representação
Gráfica das Funções