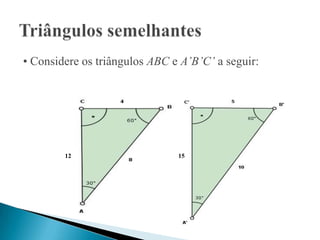
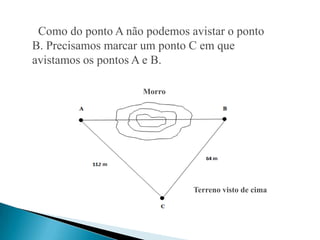
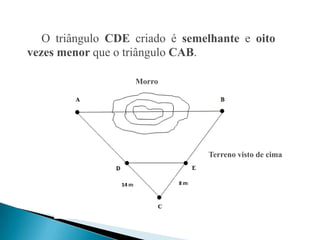
O documento descreve como determinar se dois triângulos são semelhantes, com base em ângulos correspondentes congruentes e razão entre lados correspondentes. Explica como usar a semelhança de triângulos para medir um terreno com obstáculo, dividindo as medidas por um número para obter um triângulo menor e similar.

2. • Dois triângulos são semelhantes quando têm os
ângulos correspondentes congruentes e os lados
homólogos proporcionais.

3. • Considere os triângulos ABC e A’B’C’ a seguir:
12 15

4. • os ângulos correspondentes são congruentes.
ˆ
A ˆ ˆ ˆ ˆ ˆ
A , B B , C C

5. • a razão entre os lados correspondentes é 4 .
5
AB BC AC 4
AB BC AC 5
• Podemos concluir que os triângulos ABC e A’B’C’
são semelhantes e indicamos:
ABC~ A B C

6. Denominamos:
• ângulos homólogos − os ângulos congruentes de
dois triângulos semelhantes.
ˆ ˆ ˆ ˆ ˆ ˆ
A e A , B eB , C eC

7. Denominamos:
• lados homólogos: os lados determinados
por vértices homólogos.
AB e A B , BC e B C , AC e A C

8. Se uma reta é paralela a um dos lados de um
triângulo e intercepta os outros dois em pontos
distintos, então o triângulo que ela determina é
semelhante ao primeiro.
ABC~ DEC

9. Podemos medir um terreno plano com um
obstáculo no meio com a ajuda de semelhança de
triângulos.

10. Como do ponto A não podemos avistar o ponto
B. Precisamos marcar um ponto C em que
avistamos os pontos A e B.
Morro
Terreno visto de cima

11. Fixamos então um marco em C e medimos com
a trena as distâncias AC e BC. Vamos supor que
os valores encontrados foram os seguintes:
• AC = 112 m
• BC = 64 m
Agora, vamos dividir essas distâncias por um
número fixo.

12. Por exemplo:
112 64
14 e 8
8 8
Sobre o segmento AC coloca-se um marco no
ponto D onde CD = 14 e no segmento AB coloca-
se um marco no ponto E onde CE = 8.

13. O triângulo CDE criado é semelhante e oito
vezes menor que o triângulo CAB.
Morro
Terreno visto de cima

14. Agora, através da trena o segmento DE pode ser
medido.
Se encontrarmos DE = 16 m, como sabemos que
AB é oito vezes maior, podemos concluir que AB
= 128 m.
E assim, o problema está concluído.

15. Através desse exemplo, podemos perceber que muitos
problemas envolvendo medição, seja de um terreno,
largura de um rio, altura de um prédio, podem ser
resolvidos por intermédio de semelhança de triângulos.

16. • IEZZI, Gelson et al. Matemática: volume único. São
Paulo: Atual, 1997.
• DOLCE, Osvaldo, POMPEO, José Nicolau.
Fundamentos de Matemática Elementar 9:
Geometria plana. São Paulo: Atual, 2005.