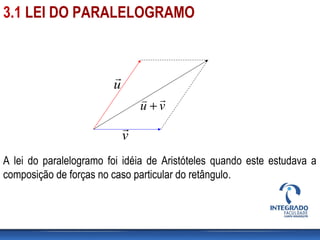
Este documento apresenta conceitos de vetores em geometria analítica e álgebra linear. Discute definições de vetores, representações gráficas e simbólicas, operações como soma, diferença, produto escalar e vetorial. Explica norma, ângulo entre vetores, vetores unitários e aplicações em R2 e R3.

1. AULA 21
GEOMETRIAANALÍTICA E
ÁLGEBRA LINEAR
Professor: João Alessandro
VETORES

2. 1 – DEFINIÇÕES

3. Vetores
– Um vetor é uma ficção, uma entidade criada para descrever
“coisas” no mundo que têm direção e sentido.
Que coisas são essas?
• o vento;
• o fluxo de H2
O de um rio;
• a emissão puntiforme de luz;
• um campo elétrico;
• a velocidade de um trem bala;
• o movimento dos planetas (aliás, a teoria de Newton não
explica por que os planetas se movem todos num mesmo
sentido), etc.
1. DEFINIÇÃO

4. 2 – REPRESENTAÇÃO

5. Para bem determinar a posição de um vetor é necessário a escolha de um
sistema de coordenadas.
Sistema de coordenadas retangulares ou cartesianas
Define-se um sistema de coordenadas cartesianas quando é dada uma unidade
linear para medir os comprimentos e dois eixos perpendiculares ordenados
numa ordem qualquer.
. P(x,y)
x
y
0 x’
y’
O ponto P(x,y) significa que o ponto P tem por abscissa o
nº x e por ordenada o n.º y.
2.1 SISTEMAS DE COORDENADAS

6. Representação gráfica
– A representação gráfica de um vetor é a de uma flecha apontando
para algum lugar.
• Propriedades
- direção;
- sentido;
- magnitude.
– Grandezas vetoriais: a aceleração, a velocidade e o deslocamento,
força, etc.
– Grandezas escalares: a massa, o tempo e a temperatura,
densidade, etc.
2.2 REPRESENTAÇÃO GRÁFICA

7. – Por convenção, para saber que estamos falando de vetores e
não de variáveis ou outro ente matemático qualquer,
designamos o vetor por uma letra e utilizamos uma flecha sobre
a letra.
– Mas há outras maneiras de representar um vetor. Imagine, por
exemplo, um vetor no plano:
u

2.3 REPRESENTAÇÃO SIMBÓLICA

8. Representação simbólica
– A sua origem e a sua extremidade podem ser associadas a pontos no plano xy.
y2
y1
x2x1
A
X
Y
B
Assim, o vetor acima pode ser representado como o segmento orientado e
seu comprimento é dado por B – A. As coordenadas de A são (x1
, y1
) e as
coordenadas de B são (x2
, y2
).
Logo, o comprimento do vetor AB é dado por B – A = (x2
- x1
, y2
-y1
)
AB
2.3.1 REPRESENTAÇÃO SIMBÓLICA ASSOCIADA A
PONTOS

9. Exemplo
– Seja = [2,2].
y2
y1
x2x1
A
X
Y
B
Podemos associar a o segmento de reta orientado com ponto inicial
A(1,2) e ponto final B(3,4).
= B – A = (3-1, 4-2)=(2,2)
u

(3,4)
(1,2)
u

u

2.3.1 REPRESENTAÇÃO SIMBÓLICA ASSOCIADA A
PONTOS

10. ),( bav =Representação:
2.4 VETORES NO R²
(2, 1)
x
0
y

11. (2, 4, 3)
x
y
z
),,( cbav =
2.5 VETORES NO R³
Representação:

12. 3 – OPERAÇÕES

13. Operações com vetores
– Considere 2 vetores: e .u

v

v

u

A resultante + é obtida pela chamada “lei do
paralelogramo”.
Construímos um paralelogramo unindo a origem dos dois
vetores e traçando retas paralelas a e a partir de
suas extremidades.
u

v

u

v

3. OPERAÇÕES

14. v

u

vu

+
A lei do paralelogramo foi idéia de Aristóteles quando este estudava a
composição de forças no caso particular do retângulo.
3.1 LEI DO PARALELOGRAMO

15. Somando mais que dois vetores
a

b
ba

+
c

cba

++
d

dcba

+++
3.1 LEI DO PARALELOGRAMO

16. • Em termos de suas coordenadas, a soma se dá componente a componente:
• Definição:Sejam e dois vetores no plano. A soma
dos vetores e é o vetor .
Exemplo:
Sejam e então,
),( 11 yxu =

),( 22 yxv =

u

v

),( 2121 yyxxvu ++=+

)2,1(=u

)4,3( −=v

)2,4())4(2,31( −=−++=+ vu

1.ª coordenada
2.ª coordenada
3.2 SOMA ALGÉBRICA

17. Representamos o vetor + (-1) por
Esse vetor é a diferença de e .
u

v

vu

−
u

v

u

v

v

−
vu

−
3.3 DIFERENÇA

18. Considere que o vetor tem a magnitude de uma unidade. Se multiplicarmos esse
vetor por um número real qualquer, por exemplo, 3, o vetor tem sua magnitude
aumentada para 3 unidades. A direção é conservada se o escalar for ≥0, caso
contrário, o vetor assume a direção oposta.
w

w

3.4 Produto de um vetor por um escalar

19. Se a = 2, b = -3 e = (1,-2), então:
e
w

)4,2()2,1(2. −=−=wa

)6,3()2,1(3. −=−−=wb

Exemplo:
3.4.1 Produto de um vetor por um escalar – forma
algébrica

20. O produto escalar dos vetores de dimensão n:
a = (a1,a2,...an) e b = (b1,b2,...,bn), é definido por:
a.b = a1b1 + a2b2 + ...+ anbn =
Exemplo
Calcule o produto escalar de = (1,-2,3,4) e = (2,3,-2,1).
. = 1.2 + (-2).3 + 3.(-2)+ 4.1 = -6
∑=
n
i
iiba
1
u

v

u

v

3.5 Produto Escalar

21. O comprimento, tamanho ou norma de um vetor = (x,y) é:u

22 yxu +=

y1
x
y
→
u
x10
3.6 COMPRIMENTO OU NORMA DE UM VETOR

22. 3.6 COMPRIMENTO OU NORMA DE UM VETOR
5
25
169
2423
22
:seránormasuaentão,(3,4)useExemplo,
=
=
+=
+=
+=
=
u
u
u
u
yxu







23. O produto escalar entre dois vetores resulta num número que mede a tendência de outro
vetor apontar na mesma direção e é dado por:
vu
vu


.
.
cos =θ
onde θ é o ângulo formado p or e .u

v

θ
u

v

3.7 Ângulo Entre Dois Vetores

24. Exemplo
Encontre o ângulo entre os vetores = (2,4) e = (-1,2).
θcos... vuvu

=
u

v

. = 2.(-1) + 4.2 = 6u

v

2042 22
=+=u

52)1( 22
=+−=v

Portanto, 6,0
5.20
6
cos ==θ
Usando a calculadora, descobrimos que o ângulo é aproximadamente 53º.
3.7 Ângulo Entre Dois Vetores

25. Ângulo entre dois vetores
→→→→
⊥⇔=⇔= vuvu 0cos0. θ
O produto escalar entre dois vetores não nulos é zero se, e só se, o cosseno do
ângulo entre eles é zero e, isto só acontece quando os vetores são perpendiculares .
Exemplo
Os vetores = (2,-4) e = (4,2)
são ortogonais, já que:
u

v

02).4(4.2. =−+=vu

3.7.1 Ângulo Entre Dois Vetores - Ortogonalidade

26. Um vetor unitário é um vetor de comprimento 1. Se é um vetor não-nulo, então o
vetor:
é um vetor unitário com a mesma direção e sentido que .
x
x
u .
1


=
x

x

3.8 Versor ou Vetor unitário

27. Exemplo
Seja x = (-3,4). Então:
Logo, o vetor
É um vetor unitário, pois:
54)3( 22
=+−=x

( ) 





+
−
=−==
5
4
5
3
4,3
5
1
.
1
x
x
u 

1
25
169
5
4
5
3
22
=
+
=





+




 −
=u

3.8 Versor ou Vetor unitário

28. 4 – PRODUTO VETORIAL

29. Produto vetorial
Diferentemente do produto escalar, que dá como resultado um número, o produto vetorial tem
como resultado, um outro vetor.
Definição: Sejam = a1
î + b1
ĵ + c1
k e = a2
î + b2
ĵ + c2
k dois vetores em ℜ3
. Seu produto vetorial é o
vetor x definido por:
222
111
cba
cba
kji
vu =×

4.PRODUTO VETORIAL

30. Produto vetorial
A igualdade anterior também pode ser escrita da seguinte forma:
Exemplo:
Sejam =2î + j + 2k e = 3î –j – 3k, então:
k
ba
ba
j
ca
ca
i
cb
cb
vu ...
22
11
22
11
22
11
+−=×

)5,12,1(5121
313
212 −−=−+−=
−−
=× kji
kji
vu

4.1 Produto Vetorial

31. DÚVIDAS?
joaoalessandro.luz@gmail.com