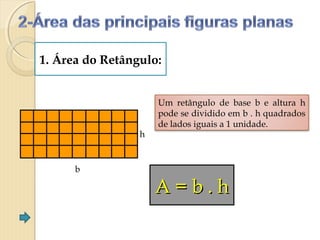
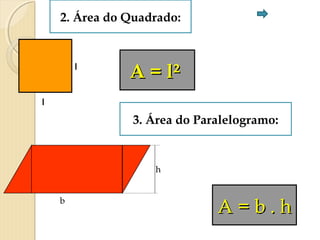
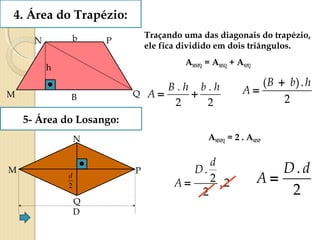
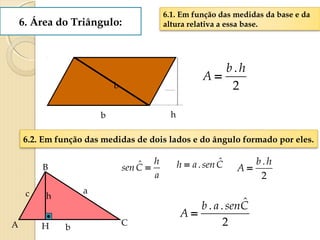
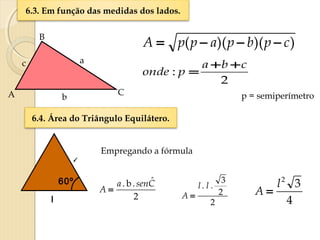
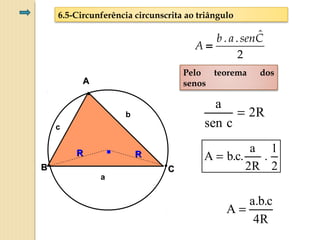
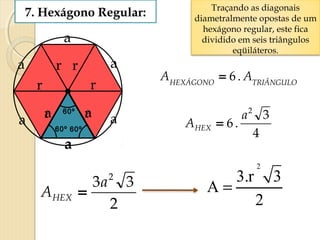
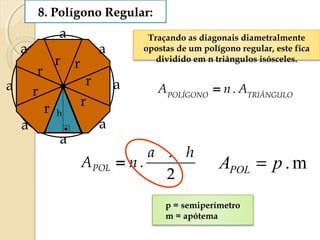
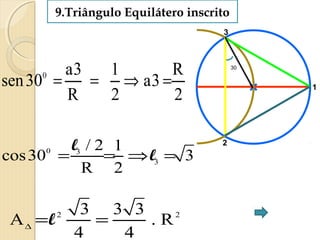
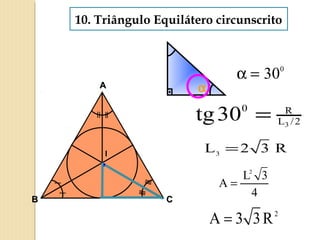
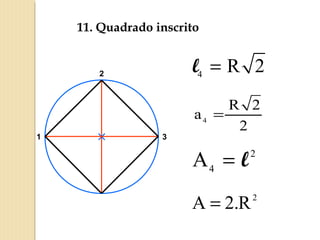
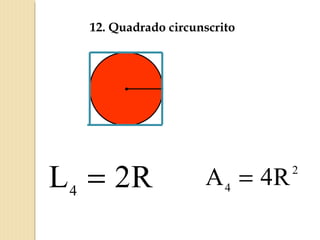
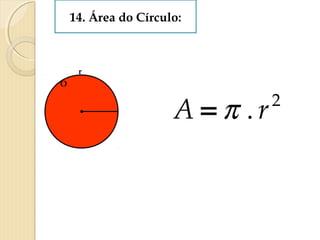
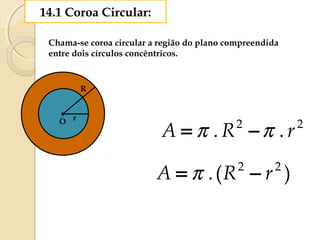
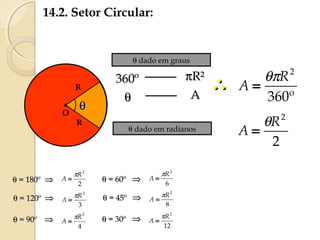
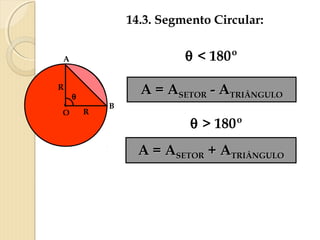
O documento apresenta fórmulas para calcular a área de várias figuras planas como retângulos, quadrados, triângulos e círculos. Inclui também a definição de área como um número real positivo associado à superfície de uma região. Explica que a área de uma figura é dada pela multiplicação de medidas como base e altura ou pelo produto de medidas de lados.

1. Áreas de
Figuras Planas

2. Área de uma superfície limitada é um número real positivo
associado à superfície de tal forma que:
Dois polígonos são chamados equivalentes se e somente se,
forem somas de igual número de polígonos dois a dois congruentes
entre si.

3. Sistema métrico
km2
– hm2
– dam2
– m2
– dm2
– cm2
– mm2
Uma unidade de área é definida como sendo a
superfície de uma região quadrada de lado
unitário.

4. 1. Área do Retângulo:
b
h
Um retângulo de base b e altura h
pode se dividido em b . h quadrados
de lados iguais a 1 unidade.
A = b . hA = b . h

5. 2. Área do Quadrado:
l
l
A = l²A = l²
3. Área do Paralelogramo:
b
h
A = b . hA = b . h

6. 4. Área do Trapézio:
b
BM Q
h
N P
Traçando uma das diagonais do trapézio,
ele fica dividido em dois triângulos.
AMNPQ = AMNQ + ANPQ
22
b . hB . h
A +=
2
d
2
.)( hbB
A
+
=
5- Área do Losango:
M
Q
N
P
2
d
D
AMNPQ = 2 . AMNP
2.
2
2
.
d
D
A =
2
.dD
A =

7. 6. Área do Triângulo:
b h
2
. hb
A =
a
h
Csen =ˆ
6.2. Em função das medidas de dois lados e do ângulo formado por eles.
b
h
a
B
A C
c
H
Csenah ˆ.=
b
2
. hb
A =
2
ˆ.. Csenab
A =
6.1. Em função das medidas da base e da
altura relativa a essa base.

8. 6.3. Em função das medidas dos lados.
b
a
B
A C
c
))()(( cpbpappA −−−=
2
ˆ.b. Csena
A =
2
:
cba
ponde
++
=
p = semiperímetro
6.4. Área do Triângulo Equilátero.
l
l
60º
Empregando a fórmula
2
2
3
. l .l
A =
4
32
l
A =

9. 6.5-Circunferência circunscrita ao triângulo
Pelo teorema dos
senos
2
ˆ.. Csenab
A =
a.b.c
A
4R
=
a
2R
sen c
=
a 1
A b.c. .
2R 2
=
CC
AA
BB
RR RR.
b
a
c

10. a
aa
a
aa
7. Hexágono Regular:
rr
rr
rr
60º
60º
60º
Traçando as diagonais
diametralmente opostas de um
hexágono regular, este fica
dividido em seis triângulos
eqüiláteros.
TRIÂNGULOHEXÁGONO
AA .6=
4
3
.6
2
a
AHEX =
2
33 2
a
AHEX =
60º
60º
60º
a
aa
2
3.r 3
A
2
=

11. 8. Polígono Regular:
Traçando as diagonais diametralmente
opostas de um polígono regular, este fica
dividido em n triângulos isósceles.
TRIÂNGULOPOLÍGONO
AnA .=
m.pAPOL =
a
aa
a
a
a
a
a
r
r
rr
r
r
r
2
.
.
ha
nAPOL =
p = semiperímetro
m = apótema
rh
a

12. 9.Triângulo Equilátero inscrito
1
2
3
30
0 3
3
/ 2 1
cos30 3
R 2
= = ⇒ =
l
l
2 23 3 3
A . R
4 4
∆
= =l
0 a3 1 R
sen30 a3
R 2 2
= = ⇒ =

13. 10. Triângulo Equilátero circunscrito
.II
AA
BB CC
α
0
30α =
3
0 R
L /2tg30 =
3
L 2 3 R=
2
L 3
A
4
=
2
A 3 3R=

14. 11. Quadrado inscrito
3
2
1
4
R 2=l
4
R 2
a
2
=
2
4
A = l
2
A 2.R=

15. 12. Quadrado circunscrito
4
L 2R= 2
4
A 4R=

16. 14. Área do Círculo:
r
O
2
.rA π=

17. 14.1 Coroa Circular:
Chama-se coroa circular a região do plano compreendida
entre dois círculos concêntricos.
rO
R
22
.. rRA ππ −=
)(. 22
rRA −= π

18. 14.2. Setor Circular:
O
R
R
360º360º ππR²R²
θθ AA º360
2
R
A
θπ
=
θ dado em graus
∴∴
θ dado em radianos
2
2
R
A
θ
=
θθ = 180º= 180º ⇒⇒ 2
2
R
A
π
=
θθ = 120º= 120º ⇒⇒
3
2
R
A
π
=
θθ = 90º= 90º ⇒⇒
4
2
R
A
π
=
θθ = 60º= 60º ⇒⇒ 6
2
R
A
π
=
θθ = 45º= 45º ⇒⇒
8
2
R
A
π
=
θθ = 30º= 30º ⇒⇒
12
2
R
A
π
=
θθ

19. 14.3. Segmento Circular:
R
R
A
B
θ
A = AA = ASETORSETOR - A- ATRIÂNGULOTRIÂNGULO
A = AA = ASETORSETOR + A+ ATRIÂNGULOTRIÂNGULO
θ < 180º
θ > 180º
O
θ